中考数学专题复习练习：正多边形和圆 9页

例 选择题：‎ ‎（1）下列叙述正确的是( )．‎ ‎ (A)各边相等的多边形是正多边形 (B)各角相等的多边形是正多边形 ‎ (C)各边相等，各角也相等的多边形是正多边形 (D)轴对称图形是正多边形 答案（C）‎ ‎（2）正多边形的每个内角与外角的关系是( )．‎ ‎ (A)内角大于外角 (B)内角小于外角 ‎ (C)内角等于外角 (D)可能大于外角，可能小于外角，也可能等于外角 答案（D）‎ ‎（3）在正三角形、正方形、正五边形、正六边形中，其中共有( )个中心对称图形．‎ ‎ (A)0 (B)l (C)2 (0)4‎ 答案（C）．‎ 说明：①巩固正多边形的概念；②在第（3）小题中，正方形和正六边形是中心对称图形，一般地，正2n边形既是轴对称图形也是中心对称图形，正2n+l边形是轴对称图形但不是中心对称图形．‎ 例 已知：如图，圆O的内接等腰三角形ABC，AB=AC，弦BD、CE分别平分∠ABC、∠ACB，BE=BC．求证：五边形AEBCD是正五边形．‎ 证明：在△ABC中，‎ ‎∵AB=AC，∴∠ABC=∠ACB，‎ 又∵BD、CE分别平分∠ABC、∠ACB，‎ ‎∴∠ABD=∠DBC=∠ACE=∠ECB，∴===，‎ 又∵BE=BC，∴=‎ ‎∴点A、E、B、C、D把圆O五等分，‎ ‎∴五边形AEBCD是正五边形．‎ 说明：①此题利用第一个定理（判断正多边形）；②应用等腰三角形、角分线、圆周角等知识．‎ 例 求证：如果一个四边形有一个外接圆和一个内切圆，并且这两个圆是同心圆，那么这个四边形是正方形．‎ 已知：如图，四边形ABCD内接于大圆O，且各边与小圆相切于点E、F、G、H．‎ 求证：四边形ABCD是正方形．‎ ‎ 证明：连结OE、OF、OG、OH．‎ ‎ ∵四边形ABCD与小圆分别切于点E、F、G、H，‎ ‎ ∴OE=OF= OG=OH=，且OE⊥AB、OF⊥BC、OG⊥CD、OH⊥AD．‎ ‎ ∴AB=BC=CD=DA．‎ ‎ ∴A、B、C、D是大圆O的四等分点．‎ ‎∴四边形ABCD是正方形．‎ 说明：①此题训练学生把文字语言转化为数学语言；②应用第一个定理、切线的性质、垂径定理等知识；③此题可以推广到边数是n的多边形．‎ 例 如图，在正六边形ABCDEF中，G是BF的中点，切GH⊥AB于H．‎ 求证AH: AB．‎ 证明：∵AB=AF，G是BF的中点，‎ ‎∴AG⊥BF，‎ 又∠BAF=，‎ ‎∴∠ABG=30°=∠AGH，‎ 设AH=x，则AG=2x，AB=4x．‎ ‎∴AH:AB=x:4x=1:4‎ 说明：此题应用正多边形的定义，直角三角形的有关性质．‎ 典型例题五 例 周长相等的正三角形、正四边形、正六边形的面积、、间的大小关系是（）‎ ‎（A） （B）‎ ‎（C） （D）‎ 解析 设它们的周长为，则正三角形的边长是，正四边形的边长为，正六边形的边长为.‎ ‎.故选B 说明：一定要注意三个正多边形的周长相等这一重要条件，否则容易得出错误结论.‎ 典型例题六 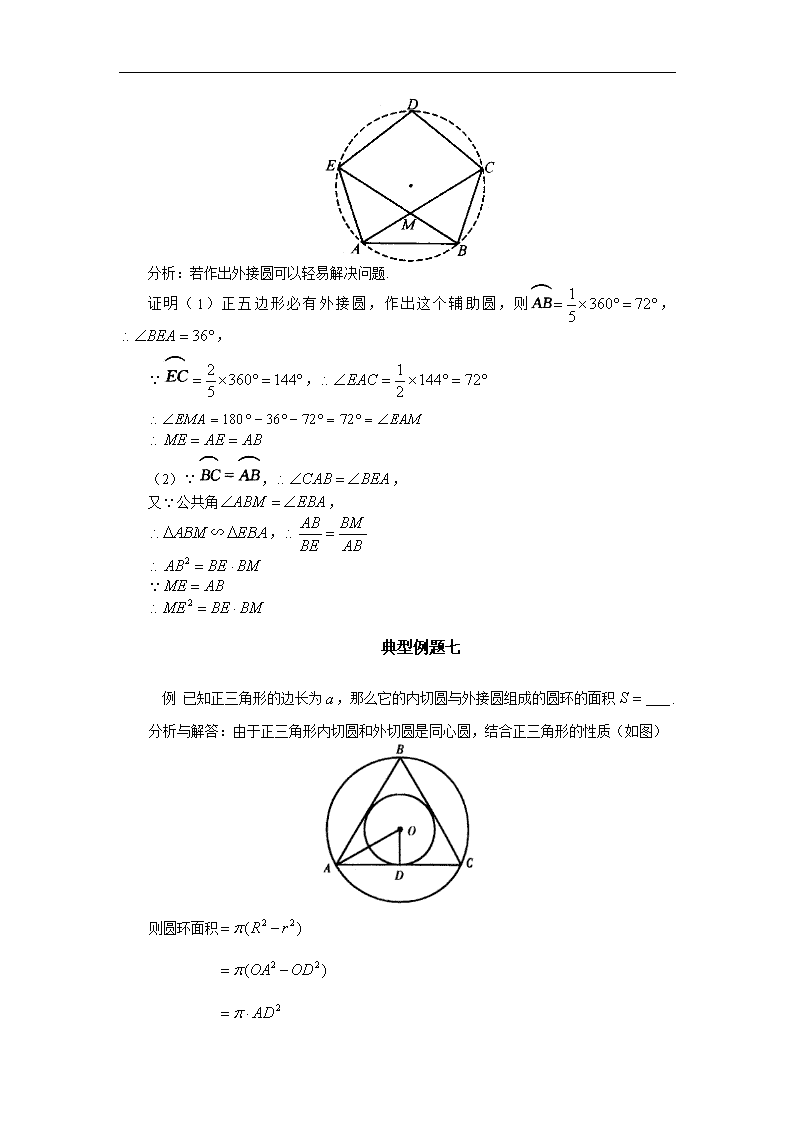例 已知：如图，正五边形的对角线和相交于点，求证：（1）；（2）.‎ 分析：若作出外接圆可以轻易解决问题.‎ 证明（1）正五边形必有外接圆，作出这个辅助圆，则，，‎ ‎，‎ ‎（2），，‎ 又公共角，‎ ‎∽，‎ 典型例题七 例 已知正三角形的边长为，那么它的内切圆与外接圆组成的圆环的面积.‎ 分析与解答：由于正三角形内切圆和外切圆是同心圆，结合正三角形的性质（如图）‎ 则圆环面积 ‎ ‎ ‎ ‎ 解之得.‎ 典型例题八 例 设计一个商标图案（如图阴影部分），矩形中，，且，以点为圆心，的长为半径作半圆，则商标图案面积等于（ ）‎ ‎（A） （B）‎ ‎（C） （D）‎ 分析与解答：仔细观察图形，阴影部分面积＝（⊙的面积＋矩形面积）－的面积.解之，选（A）.‎ 说明：在求阴影部分面积时，关键在于观察图形，将图形进行分割和组合，把不规则图形转化为可计算的规则图形.‎ 典型例题九 例 某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时，进行如下讨论：‎ ‎ 甲同学：这种多边形不一定是正多边形，如圆内接矩形；‎ ‎ 已同学：我发现达数是6时，它也不一定是正多边形．如图一，是正三角形，，可以证明六边形的各内角相等，但它未必是正六边形；‎ ‎ 丙同学：我能证明，边数是5时，它是正多边形．我想，边数是7时，它可能也是正多边形．‎ ‎ （l）请你说明乙同学构造的六边形各内角相等．‎ ‎ （2）请你证明，各内角都相等的圆内接七边形（如图二）是正七边形（不必写已知、求证）．‎ ‎ （3）根据以上探索过程，提出你的猜想（不必证明）．‎ ‎ ‎ 解：（1）由图知对. 因为，‎ ‎ 而对的 ‎ ‎ ‎ ‎ 所以. 同理可证，其余各角都等于. ‎ 所以，图1中六边形各内角相等.‎ ‎ （2）因为对，对，又因为， 所以. ‎ ‎ 所以 ‎ ‎ ‎ 同理. ‎ 所以 七边形是正七边形. ‎ ‎ （3）猜想：当边数是奇数时（或当边数是3，5，7，9……时），各内角相等的圆内接多边形是正多边形. ‎ ‎ （若仅猜想边数是某些具体奇数（不能是3，5，7）时，各内角相等的圆内接多边形是正多边形. 给1分）‎ 典型例题十 例 有两个正多边形边数比为2：1，内角度数比为4：3，求它们的边数.‎ 解 设两个正多边形的边数为，‎ 则 解得 答 它们是正五边形和正十边形.‎ 说明: 本题考查正多边形的边、角关系，掌握边角关系计算公式是解题关键.‎ 典型例题十一 例 下图中，不是中心对称的图形是（ ）‎ ‎ 解 A，C，D相当于边数是偶数的正多边形，因此是中心对称图形，B相当于边数是奇数的正多边形（具体地说相当于正三角形），所以不是中心对称图形，选B．‎ ‎ 说明:本题可以理解为是考查正多边形的一个性质，解题关键是用类比的方法结合正多边形的性质去研究，易错点不善于将其类比于恰当的正多边形，乱选一气．‎ 选择题 ‎1．一个正三角形与一个正六边形的周长相等，则它们对应的面积比为（）‎ A．1：2 B．2：3 C．3：4 D．3：2‎ ‎2．下列图形中，是轴对称图形但不是中心对称图形的是（）‎ A．菱形 B．矩形 C．等边三角形 D．圆 ‎3．正多边形的一边所对的中心角与该正多边形的一个内角的关系是（）‎ A．两角互余 B．两角互补 C．两角互余或互补 D．不能确定 ‎4．下列命题中，其命题是（）．‎ ‎ A．各边相等的圆外切多边形是正多边形 ‎ B．各角相等的圆内接多边形是正多边形 ‎ C．顶点等分圆周的圆内接多边形是正多边形 ‎ D．两个相似的多边形是正多边形 ‎5．下列说法正确的是（）．‎ ‎ A．正多边形是轴对称图形，也是中心对称图形 ‎ B．半径相等的两个正多边形，中心角越大，周长越大 ‎ C．两个正多边形一定相似 ‎ D．一个圆的外切正n边形与它的内接正n边形相似 ‎6．两个边数相同的正多边形周长的比不等于（）．‎ ‎ A．边长的比B、半径的比C．边心距的比D．面积的比 ‎7．一个正多边形的一个内角是144°，这个正多边形是（）．‎ ‎ A．正七边形B．正八边形C．正九边形D．正十边形 ‎8．四边形的外接圆和内切圆是同心圆，这样的四边形是（）．‎ ‎ A．平行四边形B．矩形C．菱形D．正方形 ‎9．如图，正六边形内接于⊙O，则的度数是（ ）‎ A．60° B．45° C．30° D．22.5°‎ ‎10．钝角三角形最长边为C，外接圆半径为R，要剪一个圆形纸片盖住这个三角形，则这个纸片的最小半径是（ ）。‎ A．R B．2R C． D．C 参考答案：‎ ‎1．B 2. C 3. B. 4. C 5. D 6. D 7. D 8. D 9 ．C 10．C.‎ 填空题 ‎1. 正n边形的内角和为　　　　，每一个内角都等于 ，每一个外角都等于 .‎ ‎2. 正n边形的一个外角为24°，那么n= ，若它的一个内角为135°，则n= ．‎ ‎3. 若一个正n边形的对角线的长都相等，则n= ．‎ ‎4. 正八边形有 条对称轴，它不仅是 对称图形，还是 对称图形．‎ ‎5. 若一个正多边形的外角大于它的一个内角，则它的边数为 ．‎ ‎6. 两个相似正多边形的面积比是9﹕4，则多边形对应边之比是 ．‎ ‎7. 已知：正三角形的边长为，则它的外接圆和内切圆组成的圆环面积是_______‎ ‎8. 如果一个正多边形的每个内角都等于，则这个正多边形的边数是________‎ ‎9. 若正多边形的内角和是，那么这个多边形是正_____边形。‎ ‎10. 有一个边长为的正六边形，若要剪一张圆形纸片完全盖住这个图形，则这个圆形纸片的最小半径是_______.‎ ‎11. 正多边形有两个特征：一是________相等，二是________相等。‎ ‎12. 中心角为72°的正多边形是正________边形。‎ ‎13. 正五边形共有_____条对称轴，______条对角线；正六边形共有______条对角线，_________条对称轴．‎ ‎14. 边数相同的两个正n边形周长之比是，则它们的面积比是______．‎ ‎15. 若已知圆的半径为2，那么它的内接三角形的边长；外切正三角形的边长是_________；它的内切正方形的边长；外切正方形的边长是__________．‎ ‎16. 某外角等于内角的的正多边形是_________．‎ ‎17. 一个正五边形，绕它的中心至少要转_________，才能和原来的正五边形重合，在不超过360°的角度内，这样的角度有________个．‎ ‎18. 一个内角为156°的正多边形是_____边形．‎ ‎19．如图，有一边长为2cm的正六边形，若要剪一张圆形纸片完全盖住这个图形，则这个图形纸片的最小半径是________。‎ 参考答案:‎ ‎1. （n-2）180°、（n-2）180°/n 、　360°/n　；2. 15、8；3. 4或5；4. 8、轴、中心 ;5. 3 ; 6. 3:2. 7. 8. 10 9. 五 10. 2cm.. 11. 各边，各角 12. 五 13. 5，5，6，9 14. 3：2 15. ；4 16. 正五边形 17. 72，5 18. 正十五 19．cm..‎ 判断题 ‎（1）各边都相等的多边形是正多边形．（ ）‎ ‎（2）每条边都相等的圆内接多边形是正多边形．（ ）‎ ‎（3）每个角都相等的圆内接多边形是正多边形．（ ）‎ ‎（4）所有正多边形都有对称中心．（ ）‎ ‎（5）有一对角相等两个正多边形相似．（ ）‎ 参考答案：‎ 判断题：（1）×；（2）√；（3）√；（4）×；（5）√.‎ 解答题 ‎1．已知正五边形，求证：对角线 ‎2．已知正六边形的对角线与对角线、分别交于、，求证：‎ ‎3. 求证：一个六边形有一个外接圆和一个内切圆，并且这两个圆是同心圆，那么这个六边形是正六边形． ‎ ‎4．甲、乙两个正多边形中，甲的边数是乙的边数的2倍，甲的一个内角与乙的一个内角的比是9：8，求甲、乙两个正多边形的边数．‎ ‎5．如图，正六边形ABCDEF的对角线BF，与对角线AC，AE交于G，H．求证：‎ ‎6．将正各边三等分，设分点为求证：是正六边形．‎ ‎7．正多边形的内角度数为，外角为，旦，求这个正多边形的边数．‎ ‎ ‎ 参考答案:‎ ‎1．作正五边形的外接圆，有，，，有.‎ ‎2．略 ‎3. 已知：如图，同心圆⊙O分别为六边形ABCDEF内切圆和外接圆，切点分别为A’、B’、C’、D’、E’、F’．‎ 求证：六边形ABCDEF是正六边形．‎ 证明：连结OA’、OB’、OC’、OD’、OE’、OF’．‎ ‎∵六边形ABCDEF有内切圆O．‎ ‎∴OA’⊥AB、OB’⊥BC、OC’⊥CD、OD’⊥DE、OE’⊥EF、OF’⊥‎ FA ．‎ 又∵六边形ABCDEF有外接圆O．‎ ‎∴AB=BC=CD=DE=EF=FA． ∴=====‎ ‎∴A、B、C、D、E、F是⊙O的六等分点，∴六边形ABCDEF是正六边形．‎ 说明：（1）考察学生的数学表达能力；（2）正多边形的判断和证明能力．‎ ‎4．甲边数为20，乙边数为10‎ ‎5．作正六边形的外接圆O，则，∴，∴，又；∴。即 ‎6．略 .7．6.‎ 作图题 ‎(1)已知：如图，正三角形，求作：正三角形ABC的外接圆和内切圆。‎ ‎(2)已知：如图，正五边形，求作：正五边形的外接圆和内切圆。(要求：保留痕迹，不写作法)‎ 参考答案：‎ ‎ 略.‎