中考数学专题复习练习：圆与圆的位置关系 4页

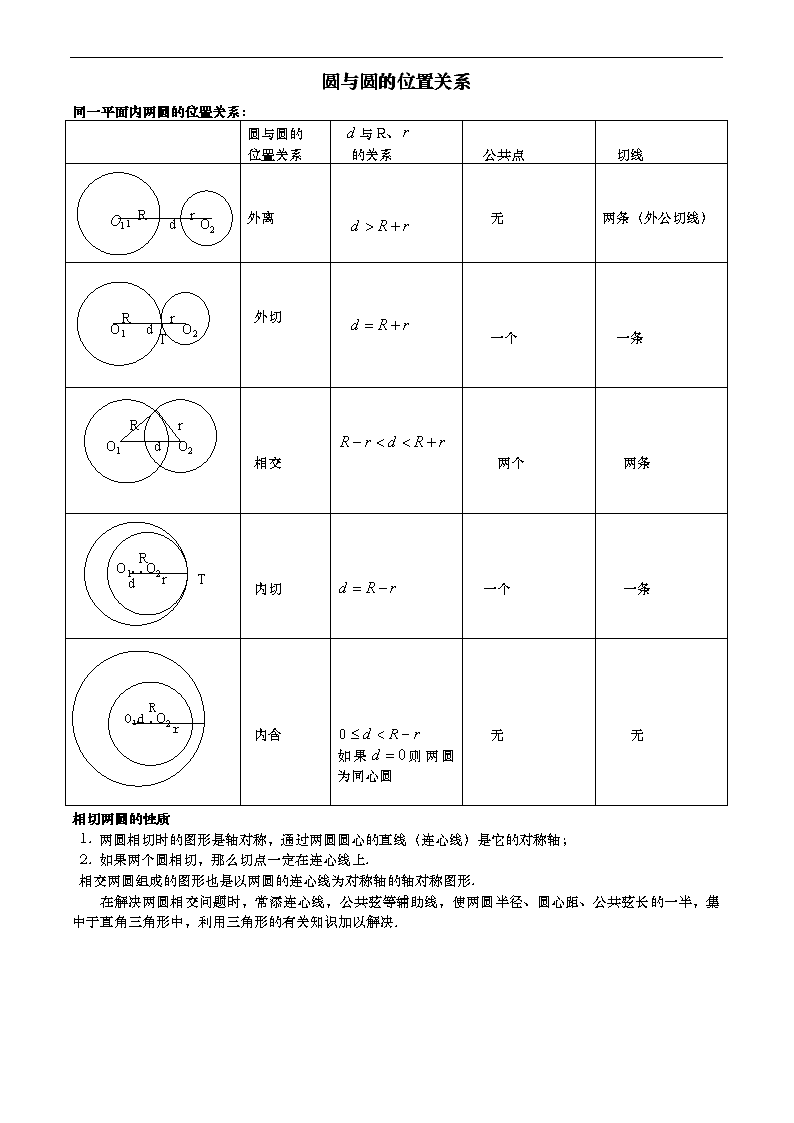
圆与圆的位置关系 同一平面内两圆的位置关系：‎ 圆与圆的 位置关系 ‎ 与R、‎ 的关系 公共点 切线 ‎1 ‎ R ‎ d ‎ O2 ‎ r ‎ 外离 无 两条（外公切线）‎ O11‎ O2 ‎ R ‎ r ‎ d ‎ T ‎ 外切 一个 一条 O1 ‎ O2 ‎ r ‎ R ‎ d ‎ ‎ 相交 两个 两条 O1. ‎ ‎.O2 ‎ d ‎ R ‎ r ‎ T ‎ ‎ 内切 一个 一条 ‎.O2 ‎ O1. ‎ d ‎ r ‎ R ‎ ‎ 内含 如果则两圆为同心圆 无 ‎ 无 相切两圆的性质 ‎1. 两圆相切时的图形是轴对称，通过两圆圆心的直线（连心线）是它的对称轴；‎ ‎2. 如果两个圆相切，那么切点一定在连心线上.‎ 相交两圆组成的图形也是以两圆的连心线为对称轴的轴对称图形.‎ 在解决两圆相交问题时，常添连心线，公共弦等辅助线，使两圆半径、圆心距、公共弦长的一半，集中于直角三角形中，利用三角形的有关知识加以解决.‎ 考点精析 类型1. 判断两圆的位置关系 例1．若相交两圆的半径分别是和，则这两个圆的圆心距可取整数值的个数是（ ）‎ A. 1 B. ‎2 ‎‎ C. 3 D. 4‎ 例2. 已知两圆相交，这两圆的半径分别为1和3，则圆心距d为（ ）‎ ‎ A. B. C. D. ‎ 例3. 已知：两圆的半径分别为R和r（，两圆的圆心距为d，当时，试判断两圆的位置关系.‎ 练习：‎ ‎1. 已知⊙O1和⊙O2的半径分别为‎2cm和‎5cm，且＝‎6 cm，则⊙O1和⊙O2的位置关系是（ ）‎ A. 内切 B. 相交 C. 外切 D. 外离 ‎2. ⊙O1和⊙O2的半径分别为3和6，当圆心距在 范围内变化时，两圆无公共点.‎ ‎3. 两圆半径分别为的两个根，当两圆外切时，圆心距等于 ，当两圆内切时，圆心距为 .‎ 类型2. 与圆有关的计算 例1. 如图，⊙O1与半径为4的⊙O2内切于点A，⊙O1经过圆心O2，作⊙O2的直径BC交⊙O1于点D，EF为过点A的切线、若O2D＝，则∠BAF等于 度.‎ 例2. 已知⊙A、⊙B相切，圆心距为‎10cm ，其中⊙A的半径为‎4 cm，求⊙B的半径.‎ 变式题：两圆的半径比为2：3，内切时的圆心距等于‎8 cm，那么这两圆相交时圆心距的范围是多少？‎ 例3. 半径分别为‎3 cm和‎4 cm的两圆相交，若公共弦长为‎4.8 cm，求两圆的圆心距.‎ A ‎ C ‎ B ‎ 练习：‎ ‎1. 如图，两个圆相外切，并且都内切于同一个大圆，已知连接三个圆 的圆心所组成的三角形周长等于‎36 cm ( )‎ A. ‎36 cm B. ‎24 cm C. ‎18 cm D. ‎‎9 cm ‎2. 如图⊙A与⊙B相交于P、Q两点，且AP是⊙B的切线，若AP=6,AB=10，求公共弦PQ的长.‎ A ‎ B ‎ P ‎ Q ‎ 类型3. 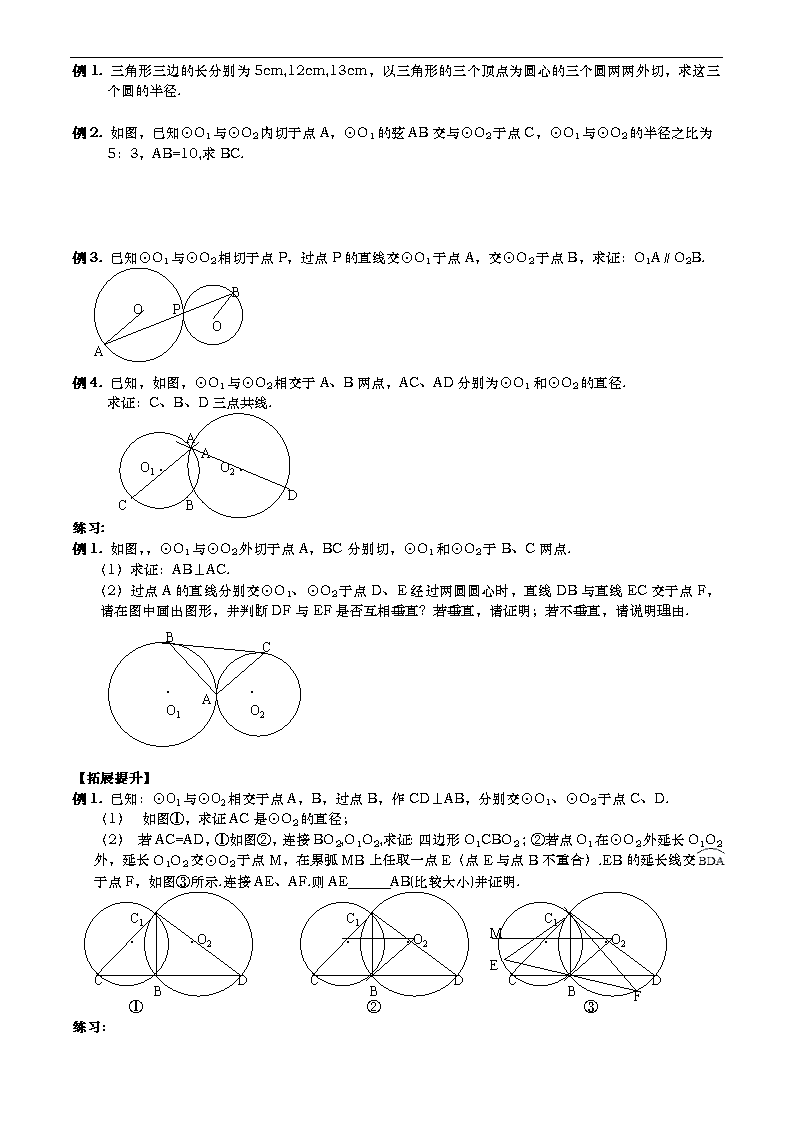与两圆相切有关的证明 例1. 三角形三边的长分别为‎5cm,‎12cm,‎13cm，以三角形的三个顶点为圆心的三个圆两两外切，求这三个圆的半径.‎ 例2. 如图，已知⊙O1与⊙O2内切于点A，⊙O1的弦AB交与⊙O2于点C，⊙O1与⊙O2的半径之比为 ‎5：3，AB=10,求BC.‎ 例3. 已知⊙O1与⊙O2相切于点P，过点P的直线交⊙O1于点A，交⊙O2于点B，求证：O‎1A∥O2B.‎ A ‎ P ‎ B ‎ O1 ‎ O2 ‎ 例4. 已知，如图，⊙O1与⊙O2相交于A、B两点，AC、AD分别为⊙O1和⊙O2的直径.‎ ‎ 求证：C、B、D三点共线.‎ A ‎ C ‎ A ‎ BC ‎ D ‎ O2 .. ‎ O1 .. ‎ 练习:‎ 例1. 如图，，⊙O1与⊙O2外切于点A，BC分别切，⊙O1和⊙O2于B、C两点.‎ ‎ （1）求证：AB⊥AC. ‎ ‎ （2）过点A的直线分别交⊙O1、⊙O2于点D、E经过两圆圆心时，直线DB与直线EC交于点F，请在图中画出图形，并判断DF与EF是否互相垂直？若垂直，请证明；若不垂直，请说明理由.‎ B ‎ C ‎ A ‎ ‎. ‎ O1 ‎ ‎ ‎ ‎. ‎ ‎. ‎ O2 ‎ ‎ ‎ ‎. ‎ ‎【拓展提升】‎ 例1. 已知：⊙O1与⊙O2相交于点A，B，过点B，作CD⊥AB，分别交⊙O1、⊙O2于点C、D.‎ （1） 如图①，求证AC是⊙O2的直径；‎ ‎（2） 若AC=AD，①如图②，连接BO2,O1O2,求证：四边形O1CBO2 ; ②若点O1在⊙O2外延长O1O2外，延长O1O2交⊙O2于点M，在累弧MB上任取一点E（点E与点B不重合）.EB的延长线交 ‎ 于点F，如图③所示.连接AE、AF.则AE AB(比较大小)并证明.‎ C ‎ B ‎ D ‎ C1 ‎ ‎. ‎ ‎.O2 ‎ E ‎ F ‎ M ‎ C ‎ B ‎ D ‎ C1 ‎ ‎. ‎ ‎.O2 ‎ C ‎ B ‎ D ‎ C1 ‎ ‎. ‎ ‎.O2 ‎ ‎ ① ② ③‎ 练习：‎ ‎1. 已知：如图，⊙O1与⊙O2外切于点A，直线与⊙O1、⊙O2分别切于B、C点，若⊙O1的半径r=‎2 cm，⊙O2的半径R=‎3 cm. 求：BC的长.‎ A ‎ O1 . ‎ O2 . ‎ B ‎ C ‎ ‎ ‎ ‎2. 如图，⊙O1与边长分别为‎18cm、‎25cm的矩形CDEF三边相切，⊙O1与⊙O2外切，且与EC、CD相切，求⊙O2的半径.‎ O1 ‎ ‎ . ‎ O2 ‎ ‎ . ‎ C ‎ D ‎ E ‎ F ‎ 类型4. 利用圆与圆的位置关系进行测量计算 例1. 某人用如下方法测一钢管的内经：将一小段钢管竖直放在平台上，向内放入两个半径为‎5 cm的钢球，测得上面一个钢球顶部高DC＝‎16cm（钢管的轴截面积如图），则钢管的内直径AD长为多少cm？‎ A ‎ B ‎ C ‎ D ‎ ‎.O1 ‎ O2 ‎ ‎ . ‎