中考数学专题复习练习：相似三角形与圆 5页

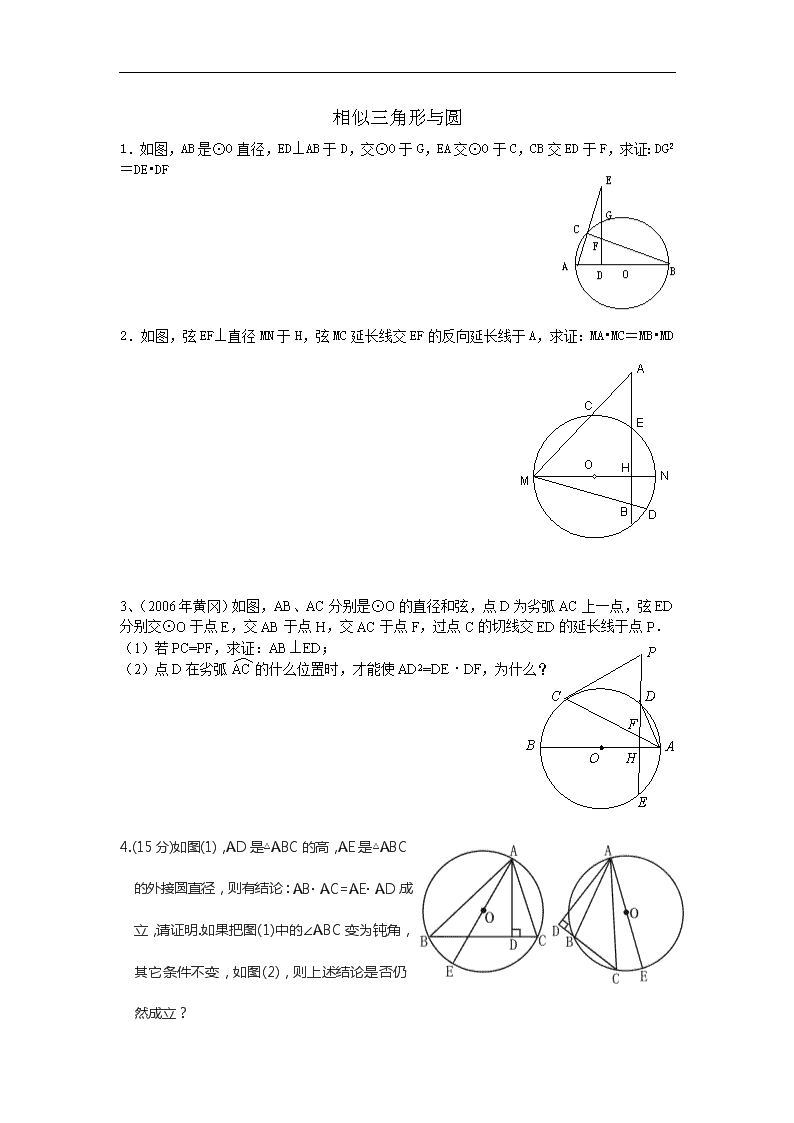
相似三角形与圆 ‎1．如图，AB是⊙O直径，ED⊥AB于D，交⊙O于G，EA交⊙O于C，CB交ED于F，求证：DG2＝DE•DF ‎2．如图，弦EF⊥直径MN于H，弦MC延长线交EF的反向延长线于A，求证：MA•MC＝MB•MD A B C P E D H F O ‎3、（2006年黄冈）如图，AB、AC分别是⊙O的直径和弦，点D为劣弧AC上一点，弦ED分别交⊙O于点E，交AB于点H，交AC于点F，过点C的切线交ED的延长线于点P．‎ ‎（1）若PC=PF，求证：AB⊥ED；‎ ‎（2）点D在劣弧AC的什么位置时，才能使AD2=DE·DF，为什么？‎ ‎4.(15分)如图(1)，AD是△ABC的高，AE是△ABC的外接圆直径，则有结论：AB· AC=AE· AD成立，请证明.如果把图(1)中的∠ABC变为钝角，其它条件不变，如图(2)，则上述结论是否仍然成立？ ‎ 图(1) 图(2)‎ ‎5.(12分)如图，AD是△ABC的角平分线，延长AD交△ABC的外接圆O于点E，过点C、D、E三点的⊙O1与AC的延长线交于点F，连结EF、DF.‎ ‎(1)求证：△AEF∽△FED；‎ ‎(2)若AD=8，DE=4，求EF的长.‎ ‎6.(15分)如图，PC与⊙O交于B，点A在⊙O上，且∠PCA=∠BAP.‎ ‎(1)求证：PA是⊙O的切线.‎ ‎(2)△ABP和△CAP相似吗？为什么？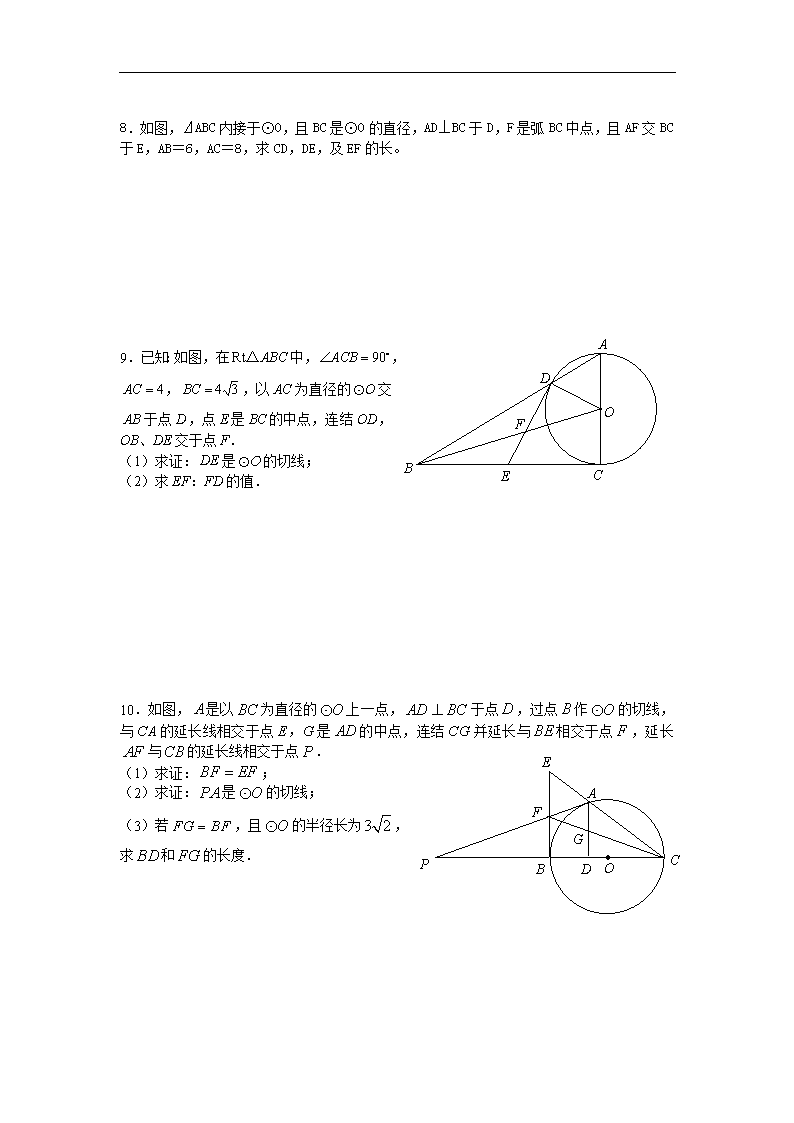‎ ‎(3)若PB:BC=2:3，且PC=20，求PA的长.‎ ‎7．（本小题满分7分）‎ 已知：如图， AD是⊙O的弦，OB⊥AD于点E，交⊙O于点C，OE=1，BE=8，AE:AB=1:3．‎ ‎　　（1）求证：AB是⊙O的切线；‎ ‎（2）点F是ACD上的一点，当∠AOF=2∠B时，求AF的长．‎ ‎ ‎ ‎8．如图，⊿ABC内接于⊙O，且BC是⊙O的直径，AD⊥BC于D，F是弧BC中点，且AF交BC于E，AB＝6，AC＝8，求CD，DE，及EF的长。‎ ‎9． 已知：如图，在中，，，，以为直径的交于点，点是的中点，连结OD，OB、DE交于点F．‎ ‎（1）求证：是的切线；‎ ‎（2）求EF：FD的值．‎ O D G C A E F B P ‎10．如图，是以为直径的上一点，于点，过点作的切线，与的延长线相交于点是的中点，连结并延长与相交于点，延长与的延长线相交于点．‎ ‎（1）求证：；‎ ‎（2）求证：是的切线；‎ ‎（3）若，且的半径长为，求和的长度．‎ ‎4.答：.连接BE，证△ABE∽△ADC图(2)同理可证，结论仍成立；‎ ‎5.答：.(1)连接EC，可证∠DFE=∠DCE，又 ‎∠DCE=∠BAE=∠CAE，从而△AEF∽△FED；(2)EF=；‎ ‎6.答：.(1)作直径AC，连接BC，证∠PAC=90即可；(2)△ABP∽△CAP，理由略；(3)PA=4 ‎ ‎10．（1）证明：是的直径，是的切线，‎ ‎．‎ 又，．‎ 易证，．‎ O D G C A E F B P Ｈ ‎．‎ ‎．‎ 是的中点，‎ ‎．‎ ‎．‎ ‎（2）证明：连结．‎ 是的直径，．‎ 在中，由（1），知是斜边的中点，‎ ‎．‎ ‎．‎ 又，．‎ 是的切线，．‎ ‎，‎ 是的切线．‎ ‎（3）解：过点作于点．‎ ‎，‎ ‎．‎ 由（1），知，．‎ 由已知，有，，即是等腰三角形．‎ ‎，．‎ ‎，‎ ‎，即．‎ ‎，‎ 四边形是矩形，．‎ ‎，易证．‎ ‎，即．‎ 的半径长为，．‎ ‎．‎ 解得．‎ ‎．‎ ‎，．‎ ‎．‎ 在中，，，‎ 由勾股定理，得．‎ ‎．‎ 解得（负值舍去）．‎ ‎．‎ ‎［或取的中点，连结，则．易证，‎ ‎，故，．‎ 由，易知，．‎ 由，解得．‎ 又在中，由勾股定理，得，‎ ‎（舍去负值）．］‎