二次函数导学案(1)二次函数 y＝ax2的图象与性质 5页

第二十二章 二次函数 第2课时 二次函数y＝ax2的图象与性质 一、阅读课本： ‎ 二、学习目标：‎ ‎1．知道二次函数的图象是一条抛物线；‎ ‎2．会画二次函数y＝ax2的图象；‎ ‎3．掌握二次函数y＝ax2的性质，并会灵活应用．‎ 三、探索新知：‎ 画二次函数y＝x2的图象．‎ ‎【提示：画图象的一般步骤：①列表（取几组x、y的对应值；②描点（表中x、y的数值在坐标平面中描点（x，y）；③连线（用平滑曲线）．】‎ 列表：‎ x ‎…‎ ‎－3‎ ‎－2‎ ‎－1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎…‎ y＝x2‎ ‎…‎ ‎…‎ 描点，并连线 由图象可得二次函数y＝x2的性质：‎ ‎1．二次函数y＝x2是一条曲线，把这条曲线叫做______________．‎ ‎2．二次函数y＝x2中，二次函数a＝_______，抛物线y＝x2的图象开口__________．‎ ‎3．自变量x的取值范围是____________．‎ ‎4．观察图象，当两点的横坐标互为相反数时，函数y值相等，所描出的各对应点关于________对称，从而图象关于___________对称．‎ ‎5．抛物线y＝x2与它的对称轴的交点（ ， ）叫做抛物线y＝x2‎ 5‎ 的_________．‎ ‎ 因此，抛物线与对称轴的交点叫做抛物线的_____________．‎ ‎6．抛物线y＝x2有____________点（填“最高”或“最低”） ．‎ 四、例题分析 例1 在同一直角坐标系中，画出函数y＝x2，y＝x2，y＝2x2的图象．‎ 解：列表并填：‎ x ‎…‎ ‎－4‎ ‎－3‎ ‎－2‎ ‎－1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎…‎ y＝x2‎ ‎…‎ ‎…‎ y＝x2的图象刚画过，再把它画出来．‎ x ‎…‎ ‎－2‎ ‎－1.5‎ ‎－1‎ ‎－0.5‎ ‎0‎ ‎0.5‎ ‎1‎ ‎1.5‎ ‎2‎ ‎…‎ y＝2x2‎ ‎…‎ ‎…‎ 归纳：抛物线y＝x2，y＝x2，y＝2x2的二次项系数a_______0；顶点都是__________；‎ ‎ 对称轴是_________；顶点是抛物线的最_________点（填“高”或 5‎ ‎“低”） ．‎ 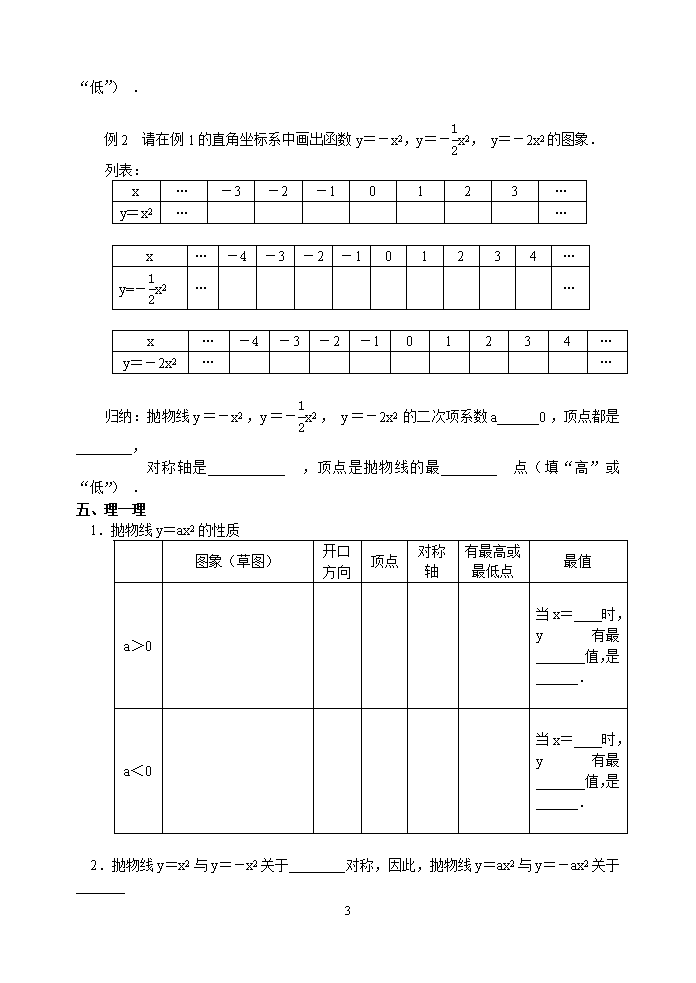例2 请在例1的直角坐标系中画出函数y＝－x2，y＝－x2， y＝－2x2的图象．‎ 列表：‎ x ‎…‎ ‎－3‎ ‎－2‎ ‎－1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎…‎ y＝x2‎ ‎…‎ ‎…‎ x ‎…‎ ‎－4‎ ‎－3‎ ‎－2‎ ‎－1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎…‎ y=－x2‎ ‎…‎ ‎…‎ x ‎…‎ ‎－4‎ ‎－3‎ ‎－2‎ ‎－1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎…‎ y＝－2x2‎ ‎…‎ ‎…‎ 归纳：抛物线y＝－x2，y＝－x2， y＝－2x2的二次项系数a______0，顶点都是________，‎ ‎ 对称轴是___________，顶点是抛物线的最________点（填“高”或“低”） ．‎ 五、理一理 ‎1．抛物线y＝ax2的性质 图象（草图）‎ 开口 方向 顶点 对称轴 有最高或最低点 最值 a＞0‎ 当x＝____时，y有最_______值，是______．‎ a＜0‎ 当x＝____时，y有最_______值，是______．‎ ‎2．抛物线y＝x2与y＝－x2关于________对称，因此，抛物线y＝ax2与y＝－ax2关于_______‎ 5‎ ‎ 对称，开口大小_______________．‎ ‎3．当a＞0时，a越大，抛物线的开口越___________；‎ ‎ 当a＜0时，｜a｜ 越大，抛物线的开口越_________；‎ ‎ 因此，｜a｜ 越大，抛物线的开口越________，反之，｜a｜ 越小，抛物线的开口越________．‎ 六、课堂训练 ‎1．填表：‎ 开口方向 顶点 对称轴 有最高或最低点 最值 y＝x2‎ 当x＝____时，y有最_______值，是______．‎ y＝－8x2‎ ‎2．若二次函数y＝ax2的图象过点（1，－2），则a的值是___________．‎ ‎3．二次函数y＝(m－1)x2的图象开口向下，则m____________．‎ ‎4．如图， ① y＝ax2‎ ‎ ② y＝bx2‎ ‎ ③ y＝cx2‎ ‎ ④ y＝dx2‎ ‎ 比较a、b、c、d的大小，用“＞”连接．‎ ‎ ___________________________________‎ 七、目标检测 ‎1．函数y＝x2的图象开口向_______，顶点是__________，对称轴是________，‎ ‎ 当x＝___________时，有最_________值是_________．‎ ‎2．二次函数y＝mx有最低点，则m＝___________．‎ ‎3．二次函数y＝(k＋1)x2的图象如图所示，则k的取值 ‎ ‎ 范围为___________．‎ ‎4．写出一个过点（1，2）的函数表达式_________________．‎ 5‎ 5‎