2013年4月普陀中考数学二模试题 9页

2012 学年度第二学期普陀区初三质量调研 数学试卷 2013.4 （时间：100 分钟，满分：150 分） 一、单项选择题：（本大题共 6 题，每题 4 分，满分 24 分） 1．下列各数中无理数共有（ ）. ①–0.21211211121111，② 3  ，③ 22 7 ，④ 8 ，⑤ 3 9 . (A) 1 个； (B) 2 个； (C) 3 个； (D) 4 个. 2. 如果 a>1>b，那么下列不等式正确的个数是（ ）. ① a–b>0，② a-1>1–b，③ a-1>b–1，④ 1a b  . (A) 1； (B) 2； (C) 3； (D) 4. 3．在下列方程中，有实数根的是（ ）. (A) 2 3 1 0xx   ； (B) 4 1 1 0x    ； (C) 2 2 3 0xx   ； (D) 1 11 x xx . 4．下列语句正确的是（ ）. (A)“上海冬天最低气温低于–5 ºC ”，这是必然事件； (B) “在去掉大小王的 52 张扑克牌中抽 13 张牌，其中有 4 张黑桃”，这是必然事件； (C) “电视打开时正在播放广告”，这是不可能事件； (D) “从由 1，2，5 组成的没有重复数字的三位数中任意抽取一个数，这个三位数能被 4 整除”，这是随机事件. 5. 上海市 2012 年 5 月份某一周的日最高气温（单位：ºC）分别为 28，30，25，29，31，32， 28，这周的日最高气温的平均值为（ ）. (A) 28ºC； (B) 29ºC； (C) 30ºC； (D) 31ºC. 6．对于一个正多边形，下列四个命题中，错误的是（ ）. （A）正多边形是轴对称图形，每条边的中垂线是它的对称轴； （B）正多边形是中心对称图形，正多边形的中心是它的对称中心； （C）正多边形每一个外角都等于正多边形的中心角； （D）正多边形每一个内角都与正多边形的中心角互补． 二、填空题：（本大题共 12 题，每题 4 分，满分 48 分） 7．计算： 3 3aa= . 8．函数 () 2 xfx x  的定义域是 . 9．若 2 ( 0)3 ac bdbd   其中 ，则 ac bd   = ． 10．某城市现有固定居住人口约为一千九百三十万，用科学计数法表示为 人. 11．不等式组 1 0, 24 x x    的解集是 ． 12. 分解因式： 227 18 3xx   . 13．如果两个相似三角形的面积之比是 16∶9，那么它们对应的角平分线之比是 . 14. 有 6 张分别写有数字 1、2、3、4、5、6 的卡片，它们的背面相同，现将它们的背面朝上， 从中任意摸出一张是数字 5 的机会是 . 15．如图，在平行四边形 ABCD 中，点 E、F 分别是 AB、CD 上 的中点，记 AB a ， AD b . 用含a 、b 的式子表示向量 AF = . 16. 为了了解中学生的身体发育情况，对第二中学同年龄的 80 名学生的身高进行了测量，经 统计，身高在 150.5—155.5 厘米之间的頻数为 5，那么这一组的頻率是 . 17．地面控制点测得一飞机的仰角为 45°，若此时地面控制点与该飞机的距离为 2000 米， 则此时飞机离地面的高度是 米（结果保留根号）. 18．已知在△AOB 中，∠B=90°，AB=OB，点 O 的坐标为（0，0），点 A 的坐标为（0，8）， 点 B 在第一象限内，将这个三角形绕原点 O 旋转 75°后，那么旋转后点 B 的坐标为 . 三、解答题（本大题共 7 题，其中第 19---22 题每题 10 分，第 23、24 题每题 12 分，第 25 题 14 分，满分 78 分） 19．计算： 012 ( 4) 2tan30 3     . A B C D E F 20．解方程组： 22 2, 2 2 2 12. 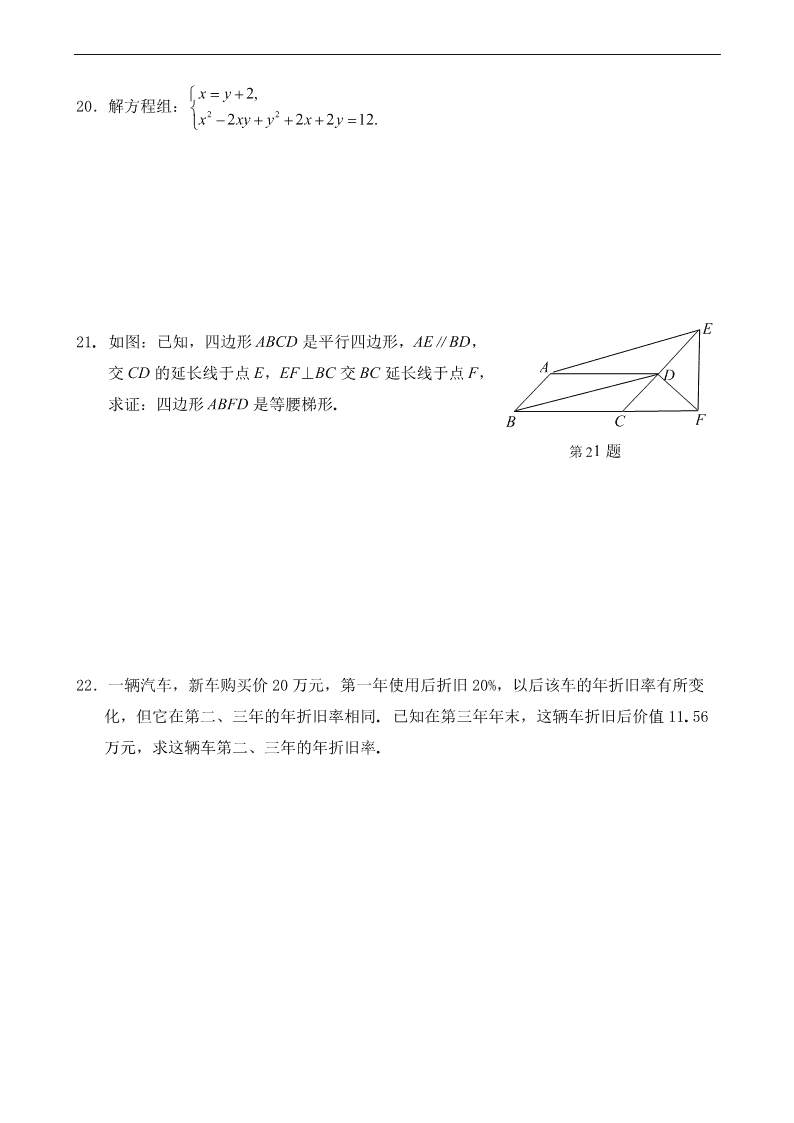xy x xy y x y        21. 如图：已知，四边形 ABCD 是平行四边形，AE∥BD， 交 CD 的延长线于点 E，EF⊥BC 交 BC 延长线于点 F， 求证：四边形 ABFD 是等腰梯形. 22．一辆汽车，新车购买价 20 万元，第一年使用后折旧 20%，以后该车的年折旧率有所变 化，但它在第二、三年的年折旧率相同. 已知在第三年年末，这辆车折旧后价值 11.56 万元，求这辆车第二、三年的年折旧率. A B C D A B C D A B C D A B D 第 21 题 C A B F E D 23．如图，已知⊙O 的半径为 5，弦 AB 的长等于 8， OD⊥AB，垂足为点 D，DO 的延长线与⊙O 相交 于点 C，点 E在弦 AB 的延长线上，CE 与⊙O 相 交于点 F，cosC= 3 5 ， 求：（1）CD 的长（5 分）；（2）EF 的长（7 分）. [来源:Zxxk.Com] 24. 如图，抛物线 cbxxy  2 经过直线 3 xy 与坐标轴的两个交点 A、B，此抛物线 与 x 轴的另一个交点为 C，抛物线的顶点为 D. （1）求此抛物线的解析式（4 分）； （2） 点 P 为抛物线上的一个动点，求使 APCS ∶ ACDS =5∶4 的点 P 的坐标（5 分）； （3）点 M 为平面直角坐标系上一点，写出使点 M、A、B、D 为平行四边形的点 M 的坐标（3 分）. D 第 23 题 A E B C O F x y O C B D A 1 第 24 题 25．如图，在 Rt△ABC 中，∠ACB=90°，AC=6cm，BC=8cm. 点 P 为 BC 的中点，动点 Q 从点 P 出发，延射线 PC 方向以 2cm/s的速度运动，以点 P 为圆心，PQ 长为半径作圆. 设 点 Q 运动的时间为 t 秒， （1）当 t=1.2 时，判断直线 AB 与⊙P 的位置关系，并说明理由；(6 分)[来源科§网 Z§ X]（2）当△AQP 是等腰三角形时，求 t 的值；(4 分) （3）已知⊙O 为 ABC 的外接圆，若⊙P 与⊙O 相切，求 t 的值. (4 分) B P C A O Q 第 25 题 2012 学年度第二学期普陀区九年级质量调研数学试卷 参考答案及评分说明 一、单项选择题：（本大题共 6 题，每题 4 分，满分 24 分） 1．(C) ； 2．(B) ； 3．(A) ； 4．(D) ； 5．(B)； 6．(B). 二、填空题：（本大题共 12 题，每题 4 分，满分 48 分） 7. –1； 8. 0x  且 2x  ； 9. 2 3 ； 10. 71.93 10 ； 11. 12x； 12．  23 3 1x  ； 13．4∶3； 14． 1 6 ； 15． b + 1 2 a ； 16． 1 16 ； 17．1000 2 ； 18．（26， 22 ）或（ 22 ，26）． 三、解答题 19．解: 原式= 32 3 1 2 ( 3)3      …………………………………………8′（各 2 分） = 43 23 . ……………………………………………………2′ 20．解： 22 2, (1) 2 2 2 12. (2) xy x xy y x y        由（1）得： 2xy. （3）……………………………………………………1′ 由（2）得： 2( ) 2( ) 12x y x y    . （4）……………………………（2+1）′ 将（3）代入（4），得： 4xy.……………………………………………………2′ 可得： 4, 2. xy xy    …………………………………………………………1′ 解方程组得： 3, 1. x y    …………………………………………………2′ ∴原方程组的解为： ……………………………………1′ 21. 证明：∵四边形 ABCD 是平行四边形， ∴AD∥BC； 第 21 题 C A B F E D AB∥CD，AB=CD. …………………3′∴AB∥DE；又∵AE∥BD， ∴四边形 ABDE 是平行四边形. ………………………1′ ∴AB=DE . ……………………………………………1′ ∴CD=DE . ………………………………………………………………………1′ ∵EF⊥BC， ∴DF=CD=DE. ………………………………1′ ∴AB=DF. ……………………………………………………………………1′ ∵CD、DF 交于点 D，∴线段 AB 与线段 DF 不平行. ……………1′ ∴四边形 ABFD 是等腰梯形. …………………………………………1′ 22．解：设这辆车第二、三年的年折旧率为 x．……………………………1′ 根据题意，可以列出方程 220(1 20%)(1 ) 11.56x   ．……4′ 整理，得 2(1 ) 0.7225x ．…………………………………………………………1′ 2 289( 1) 400x  ． ………………………………………………1′ 171 20x    ．………………………………………………1′ 解得 1 0.15x  ， 2 1.85x  （不合题意，舍去）．……………………1′ 所以 0.15x  ，即 15%x  ． 答：这辆车第二、三年的年折旧率为15% ．…………………1′ 23．解：（1）联接 AO. ……………………………………………………1′ ∵OD⊥AB，∴ 1 42AD BD AB   , …………………2′ ∵AO=5，∴OD=3. ……………………1′ ∴CD=8. …………………………………………1′ (2)过点 O 作 OH⊥HC 于点 E， ……………………………………………1′ ∴ 2CF CH .………………………………………………………………1′ 在 Rt△OCH 中， ∵cosC= 3 5 ，OC=5，∴CH=3. ……………………………………2′ 在 Rt△CDE 中， ∵cosC= 3 5 CD CE ，CD=8，∴CE= 40 11333 .……………………2′ H D 第 23 题 A E B C O F ∴EF=CE–CF= 1113 6 733 .……………………………………………1′ 24. 解：（1）∵直线 3 xy 与坐标轴的两个交点 A、B， ∴点 B（0，–3），点 A（3，0）. ………………………2′ 又∵抛物线 cbxxy  2 经过点 A、B， ∴c=3. …………………………………………………1′ 将点 A 坐标代入抛物线的解析式 ， 解得 b=–2. ……………………………………………1′ ∴抛物线的解析式是 322  xxy . （2）∵抛物线的解析式是 ，[来源:学科网 ZXXK] 可得 C（–1，0），顶点 D （1，–4）.…………………………………………2′ 因为点 P 为抛物线上的一个动点，设点 P（a， 322  aa ）， ∵ APCS ∶ ACDS =5∶4，∴ 4 5 442 1 3242 1 2    aa . ∴ =5 解得 41 a ， 22 a ； 或 5322  aa ，因为 0 ，所以无实数解. ∴满足条件的点 P 的坐标为 )5,4(1P ， )5,2(2 P .……………………………3′ （3）∵点 M、A、B、D 为平行四边形， ∴点 M 的坐标为 )1,2(1M ， )7,2(2 M ， )1,4(3 M . ……………………3′ 25. 解：（1）过点 P 作 PD⊥AB，垂足为 D. ∵∠ACB=90°，∴∠ACB=∠PDB=90°. 又∵∠ABC=∠PBD， ∴△ACB∽△PDB. ……………2′ ∵AC=6cm，BC=8cm，∴AB=10cm. ∵点 P 为 BC 的中点，∴BP=4cm. ∵ AB PB AC PD  ，解得 PD=2.4. ………………………2′ ∵t=1.2，V=2cm/s，PQ=21.2=2.4， B P C A O Q 第 25 题 D x y O C B D A 1 第 24 题 ∴PQ=PD，即⊙P 与直线 AB 相切. …………………2′ (2)当 AP=AQ 时， ∵∠ACB=90°，∴CQ=CP=4cm，∴PQ=8cm. ∴ 1t =4 秒. ……………………………1′ 当 PA=PQ 时， ∵∠ACB=90°， AC=6cm，CP=4cm，∴AP= 132 cm. ∴PQ= 132 cm. ∴ 2t = 13 秒. ……………………1′ 当 QA=QP 时， 点 Q 在线段 AP 的中垂线 QH 上，垂足为 H. ∵∠ACB=90°，∴cos∠APC= 13 132 132 4 AP PC . 又∵cos∠APC= QPQP PH 13 ，∴ 13 13213 QP ，得 PQ= 2 13 ，∴ 3t = 4 13 .…………1′ ∴当 t=4 秒或 秒或 4 13 秒时，△AQP 是等腰三角形. ………………………1′ （3）∵点 P 在⊙O 内，∴⊙P 与⊙O 只可能内切， ∵O 为 AB 中点，P 为 BC 中点，∴圆心距 OP= 2 1 AC=3cm. …………1′ ∵⊙O 是△ABC 的外接圆，∴⊙O 的半径为 5 cm ，⊙P 的半径为 PQ， ∴ 5PQ =3 当 PQ–5=3 时，PQ=8 cm ，t=4 秒；[来源:学科网 ZXXK] 当 PQ–5=–3 时，PQ=2cm，t=1 秒. ………2′ ∴当⊙P 与⊙O 相切时，t 分别为 4 秒和 1 秒. …………………1′ B P C A O 第 25 题 Q H