呼和浩特专版2020中考数学复习方案第五单元四边形第23课时多边形与平行四边形课件 31页

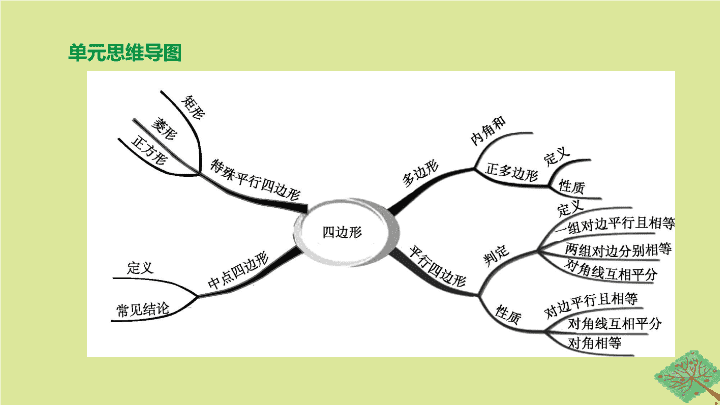
单元思维导图 第 23 课时　 多边形与平行四边形 第五单元　四边形 图形 性质 多边形 内角和 n 边形的内角和为 ① 　　 　   外角和 任意多边形的外角和为 360° 对角线 ( 1) n 边形共有 ② 　　　　 条对角线 ;  (2) 从一个顶点出发的对角线把 n 边形分成 ③ 　　　　 个三角形   不稳定性 n 边形 ( n> 3) 具有不稳定性 考点一　多边形 考点聚焦 ( n -2)·180° n -2 图形 性质 正多边形 边 各条边 ④ 　　　   内角 各个内角 ⑤ 　　　　 , 且正 n 边形的每个内角为 ⑥ 　　　　   外角 各个外角相等 , 且正 n 边形的每个外角为 ⑦ 　　　   对称性 (1) 正多边形都是 ⑧ 　　　　 对称图形 , 其中边数为偶数的正多边形也是中心对称图形 ;  (2) 正 n 边形有 ⑨ 　　　　 条对称轴   （续表） 相等 相等 轴 n 定义 　 两组对边分别平行的四边形是平行四边形 性质 (1) 平行四边形的对边 ⑩ 　　 　 ;  (2) 平行四边形的对角 ⑪ 　　　 , 邻角 ⑫ 　　　 ;  (3) 平行四边形的对角线互相 ⑬ 　　　 ;  (4) 平行四边形是 ⑭ 　　　 对称图形   判定 (1) 两组对边分别平行的四边形是平行四边形 ; (2) 两组对边分别 ⑮ 　　　 的四边形是平行四边形 ;  (3) 一组对边 ⑯ 　 　　 的四边形是平行四边形 ;  (4) 两组对角分别 ⑰ 　　　 的四边形是平行四边形 ;  (5) 对角线互相 ⑱ 　　　 的四边形是平行四边形   考点二　平行四边形 平行且相等 相等 互补 平分 中心 相等 平行且相等 相等 平分 面积 　 S=ah ( a 表示一条边长 , h 表示此边上的高 ) 相关结论 (1) 平行四边形的两条对角线将平行四边形分成 ⑲ 　　　 的四个三角形 ;  (2) 同底等高的平行四边形的面积相等 ; (3) 若一条直线过平行四边形的对角线的交点 , 则这条直线等分平行四边形的面积 （续表） 面积相等 【 温馨提示 】 (1) 多边形的外角和与边数无关 ; (2) 多边形的内角中最多有 3 个锐角 . 题组一　必会题 对点演练 1 . 将一张平行四边形的纸片折一次 , 使得折痕平分这个平行四边形的面积 , 则这样的折纸方法共有 ( 　　 ) A . 1 种 B . 2 种 C . 3 种 D . 无数种 D 2 . [2019· 威海 ] 如图 23-1, E 是 ▱ ABCD 的边 AD 延长线上一点 , 连接 BE , CE , BD , BE 交 CD 于点 F. 添加以下条件 , 不能判定四边形 BCED 为平行四边形的是 ( 　　 ) A . ∠ ABD= ∠ DCE B .DF=CF C . ∠ AEB= ∠ BCD D . ∠ AEC= ∠ CBD 图 23-1 3 . [ 八上 P24 练习第 3 题改编 ] 一个多边形的内角和与外角和相等 , 它是 　　　　 边形 .  C 四 4 . [ 八下 P51 习题 18 . 1 第 12 题改编 ] 如图 23-2, 在四边形 ABCD 中 , AD= 12, DO=OB= 5, AC= 26, ∠ ADB= 90°, 则 BC= 　　　　 , 四边形 ABCD 的面积 = 　　　　 .  图 23-2 [ 答案 ] 12 　 120 　 [ 解析 ] 在 Rt△ AOD 中 , ∠ ADB= 90°, AD= 12, OD= 5, 根据勾股定理 , 得 OA 2 =OD 2 + AD 2 = 5 2 +12 2 = 169, ∴ OA= 13 . ∵ AC= 26, OA= 13, ∴ OA=OC. 又 DO=OB , ∴四边形 ABCD 为平行四边形 , ∴ AD=BC= 12 . ∵∠ ADB= 90°, ∴ AD ⊥ BD , ∴ S 四边形 ABCD =AD · BD= 12×10 = 120 . 题组二　易错题 【 失分点 】 对平行四边形对角线性质运用不熟练 ; 忽视分类讨论或者分类讨论不全 . 5 . 已知平行四边形一边长为 10, 一条对角线长为 6, 则它的另一条对角线 a 的取值范围 ( 　　 ) A . 4