中考数学一轮复习知识点+题型专题讲义25 锐角三角形（教师版） 35页

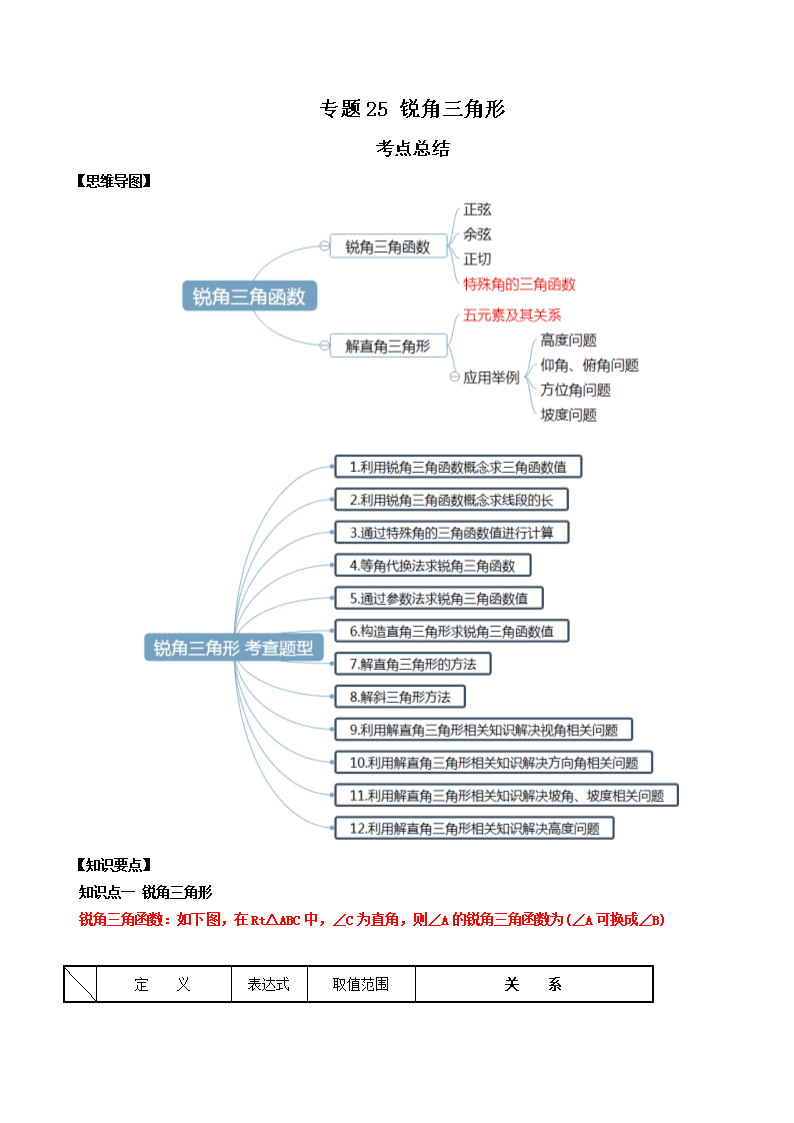
专题 25 锐角三角形 考点总结 【思维导图】 【知识要点】 知识点一 锐角三角形 锐角三角函数：如下图，在 Rt△ABC 中，∠C 为直角，则∠A 的锐角三角函数为(∠A 可换成∠B) 定 义 表达式 取值范围 关 系 正 弦 斜边 的对边AA sin c aA sin 1sin0  A (∠A 为锐角) BA cossin  BA sincos  1cossin 22  AA余 弦 斜边 的邻边AA cos c bA cos 1cos0  A (∠A 为锐角) 正 切 的邻边 的对边 Atan   AA b aA tan 0tan A (∠A 为锐角) 对 边 b ac 【正弦和余弦注意事项】 1.sinA、cosA 是在直角三角形中定义的，∠A 是锐角(注意数形结合，构造直角三角形)。 2.sinA、cosA 是一个比值（数值，无单位）。 3.sinA、cosA 的大小只与∠A 的大小有关，而与直角三角形的边长无关。 0°、30°、45°、60°、90°特殊角的三角函数值(重要) 三角函数 30° 45° 60° sin 2 1 2 2 2 3 cos 2 3 2 2 2 1 tan 3 3 1 3 锐角三角函数的关系（互余两角的三角函数关系（A 为锐角））： 1、 sin A=cos（90°-A）,即一个锐角的正弦值等于它余角的余弦值。 2、 cos A=sin（90°-A）,即一个锐角的余弦值等于它余角的余正切值。 正弦、余弦的增减性： 当 0°≤ ≤90°时，sin 随 的增大而增大，cos 随 的增大而减小。 正切的增减性：当 0°< <90°时，tan 随 的增大而增大， 【考查题型汇总】 考查题型一 利用锐角三角函数概念求三角函数值 1．（2018·南开大学附属中学中考模拟）如图，已知△ABC 的三个顶点均在格点上，则 cosA 的值为（ ） A． 3 3 B． 5 5 C． 2 3 3 D． 2 5 5 【答案】D 【详解】 过 B 点作 BD⊥AC，如图， 由勾股定理得，AB= 2 21 3 10  ，AD= 2 22 2 2 2  ， cosA= AD AB = 2 2 10 = 2 5 5 ， 故选 D． 2．（2019·福建中考模拟）如图，在 Rt ABC 中， 90C  ∠ ， 10AB  ， 8AC  ，则 sin A 等于（ ） A． 3 5 B． 4 5 C． 3 4 D． 4 3 【答案】A 【解析】 详解：在 Rt△ABC 中，∵AB=10、AC=8， ∴BC= 2 2 2 2= 10 8 =6AB AC  ， ∴sinA= 6 3 10 5 BC AB   . 故选：A． 3．（2017·天津中考模拟）如图，在平面直角坐标系中，直线 OA 过点（2，1），则 tanα的值是( ) A．2 B． 1 2 C． 5 5 D． 2 5 5 【答案】B 【解析】 根据题意可由点的坐标得到其到 x 轴的距离为 1，到 y 轴的距离为 2，因此可根据正切的意义，可得 tanα= 1= 2 对边 邻边 . 故选：B 4．（2019·天津市红光中学中考模拟）在 Rt△ABC 中，∠C=90°，sinB= 5 13 ，则 tanA 的值为（ ） A． 5 13 B． 12 13 C． 5 12 D．12 5 【答案】D 【解析】 试题解析：由 Rt ABC△ 中, 590 ,sin 13C B  o ，得 5cos sin .13A B  由 2 2sin cos 1,A A  得 2 121 cos 13sinA A   ， 12 sin 1213tan .5cos 5 13 AA A    故选 D. 5．（2019·湖南中考模拟） Rt ABC 中， C 90   ，若 BC 2 ，AC 3 ，下列各式中正确的是 ( ) A． 2sinA 3  B． 2cosA 3  C． 2tanA 3  D． 2cotA 3  【答案】C 【详解】 解： C 90  oQ ， BC 2 ， AC 3 ， AB 13  ， A. BC 2 2 13sinA AB 1313    ，故此选项错误； B. AC 3 13cosA AB 13   ，故此选项错误； C. BC 2tanA AC 3   ，故此选项正确； D. AC 3cotA BC 2   ，故此选项错误． 故选：C． 考查题型二 利用锐角三角函数概念求线段的长 1．（2018·辽宁中考模拟）在 Rt△ABC 中，∠C＝90°，AB＝6，cosB＝ 2 3 ，则 BC 的长为_____． 【答案】4 【详解】 ∵∠C=90°，AB=6， ∴ 2cos 3 BCB AB   ， ∴BC= 2 3 AB  4. 2．（2019·江苏中考真题）如图，在 ABC△ 中， 6 2BC   ， 45C  ， 2AB AC ，则 AC 的长 为________． 【答案】 2 【详解】 过 A 作 AD BC 于 D 点，设 2AC x ，则 2AB x ，因为 45C  ，所以 AD CD x  ，则由勾股定 理得 2 2 3BD AB AD x   ，因为 6 2BC   ，所以 3 6 2BC x x    ，则 2x  ．则 2AC  ． 3．（2015·上海中考模拟）在 Rt ABC 中， 90C   ，如果 6AB  ， 2cos 3A  ，那么 AC  ； 【答案】4 【解析】 因为在 Rt ABC 中， 90C   ，所以 2cos 3 ACA AB   ,所以 2 2 6 43 3AC AB    . 4．（2019·广西中考模拟）Rt△ABC 中，∠C＝90°，cosA＝ 3 5 ，AC＝6cm，那么 BC 等于_____． 【答案】8cm 【详解】 在 Rt ABC 中， Q cos ACA AB  ，   6 103cos 5 ACAB cmA    ， 则  2 2 2 210 6 8BC AB AC cm     . 故答案为8cm . 考查题型三 通过特殊角的三角函数值进行计算 1．（2019·四川中考模拟）在△ABC 中，（cosA﹣ 1 2 ）2+|tanB﹣1|＝0，则∠C＝_____． 【答案】75°． 【详解】 解：∵（cosA﹣ 1 2 ）2+|tanB﹣1|＝0， ∴cosA﹣ 1 2 ＝0，tanB﹣1＝0， 则 cosA＝ 1 2 ，tanB＝1， ∴∠A＝60°，∠B＝45°， ∴∠C＝180°﹣60°﹣45°＝75°． 故答案为：75°． 2．（2019·湖北中考真题）计算 31 27sin30 82 3       ___________． 【答案】1 3 . 【详解】 原式 1 32 3 1 2 2      1 3  ． 故答案为：1 3 ． 3．（2019·湖北中考真题）计算： 0( 2019) 2cos60    ______． 【答案】0 【详解】 0( 2019) 2cos60    = 11 2 2   =1-1 =0， 故答案为：0. 4．（2019·湖北中考模拟）2﹣1﹣ 3 tan60°+（π﹣2011）0+ 1 2 - ＝_____． 【答案】-1 【详解】 原式＝ 1 1 1 13 3 1 3 1 12 2 2 2           故答案为：﹣1． 5．（2018·四川中考真题）已知|sinA﹣ 1 2 |+ 2( 3 tan )B =0，那么∠A+∠B= ． 【答案】90° 【详解】 解：由题意可知：sinA= 1 2 ，tanB= 3 ， ∴∠A=30°，∠B=60°， ∴∠A+∠B=90° 故答案为：90° 6.（2018·湖北中考真题）计算：  22 ×2﹣2﹣| 3 tan30°﹣3|+20180=_____． 【答案】 1 2  【详解】原式=2× 1 4 ﹣| 33 3  ﹣3|+1 = 1 2 ﹣2+1 =﹣ 1 2 ， 故答案为：﹣ 1 2 ． 考查题型四 等角代换法求锐角三角函数 1．（2019·浙江中考模拟）如图，6 个形状、大小完全相同的菱形组成网格，菱形的顶点称为格点，已知菱 形的一个角（如∠O）为 60°，A，B，C，D 都在格点上，且线段 AB、CD 相交于点 P，则∠APC 的正切值 为_____． 【答案】 【详解】 解：如图取格点 E，连接 EC、DE．设小菱形的边长为 1． 由题意：EC∥AB， ∴∠APC=∠ECD， ∵∠CDO=60°，∠EDB=30°， ∴∠CDE=90°， ∵CD=2，DE= ， ∴tan∠APC=tan∠ECD= = ， 故答案为 ． 2．（2019·杭州市余杭区乾元中学中考模拟）如图，在边长相同的小正方形网格中，点 A、B、C、D 都在这 些小正方形的顶点上，AB 与 CD 相交于点 P，则 tan∠APD 的值为______. 【答案】2 【详解】 如图： ， 连接 BE， ∵四边形 BCED 是正方形， ∴DF=CF= CD，BF= BE，CD=BE，BE⊥CD， ∴BF=CF， 根据题意得：AC∥BD， ∴△ACP∽△BDP， ∴DP：CP=BD：AC=1：3， ∴DP：DF=1：2， ∴DP=PF= CF= BF， 在 Rt△PBF 中，tan∠BPF= =2， ∵∠APD=∠BPF， ∴tan∠APD=2． 故答案为：2 考查题型五 通过参数法求锐角三角函数值 1．（2019·山东中考模拟）如图，在矩形 ABCD 中，点 E 是边 BC 的中点，AE⊥BD，垂足为 F，则 tan∠BDE 的值是（ ） A． 2 4 B． 1 4 C． 1 3 D． 2 3 【答案】A 【详解】 ∵四边形 ABCD 是矩形， ∴AD=BC，AD∥BC， ∵点 E 是边 BC 的中点， ∴BE= 1 2 BC= 1 2 AD， ∴△BEF∽△DAF， ∴ 1 2 EF BE AF AD   ， ∴EF= 1 2 AF， ∴EF= 1 3 AE， ∵点 E 是边 BC 的中点， ∴由矩形的对称性得：AE=DE， ∴EF= 1 3 DE，设 EF=x，则 DE=3x， ∴DF= 2 2 =2 2DE EF x， ∴tan∠BDE= 2 42 2x EF x DF   . 故选 A． 2．（2019·山西中考模拟）在 Rt ABC 中，∠C=90°， 3sin 5A  ，则 tan B 的值为（ ） A． 4 5 B． 3 5 C． 3 4 D． 4 3 【答案】D 【详解】 解：在 Rt△ABC 中，∠C=90°， ∵sinA= BC AB = 3 5 ，设 BC=3x，则 AB=5x， ∵BC2+AC2=AB2 ∴AC=4x． ∴tanB= AC BC ＝ 4x 3x ＝ 4 3 ． 故选 D． 3．（2016·湖南中考真题）如图，在 Rt△ABC 中，∠C＝90°，sinA＝ 4 5 ，AC＝6cm，则 BC 的长度为( ) A．6cm B．7cm C．8cm D．9cm 【答案】C 【详解】 已知 sinA= 4 5 BC AB  ，设 BC=4x，AB=5x， 又因 AC2+BC2=AB2， 即 62+（4x）2=（5x）2， 解得：x=2 或 x=﹣2（舍）， 所以 BC=4x=8cm， 故答案选 C． 4．（2019·四川中考模拟）已知在 Rt△ABC 中，∠C＝90°，sinA＝ 3 5 ，则 tanB 的值为( ) A． 4 3 B． 4 5 C． 5 4 D． 3 4 【答案】A 【详解】 sinA＝ 3 5 设三边分别为 BC=3x，AC=4x，AB=5x tanB= 4 4 3 3 AC x BC x   故选 A 考查题型六 构造直角三角形求锐角三角函数值 1．（2019·广西中考模拟）∠BAC 放在正方形网格纸的位置如图，则 tan∠BAC 的值为（ ） A． 1 6 B． 1 5 C． 1 3 D． 1 2 【答案】D 【详解】 连接 CD，如图： 2 22 2 2 2AD    ，CD= 2 21 1 2  ，AC= 2 23 1 10  ． ∵ 2 2 22 2 2 10 （ ） （ ） （ ），∴∠ADC=90°，∴tan∠BAC= 2 2 2 CD AD  = 1 2 ． 故选 D． 2．（2019·湖北中考真题）如图，在5 4 的正方形网格中，每个小正方形的边长都是1， ABC 的顶点都在 这些小正方形的顶点上，则sin BAC 的值为（ ） A． 4 3 B． 3 4 C． 3 5 D． 4 5 【答案】D 【详解】 如图，过 C 作CD AB 于 D ，则 =90ADC ，  2 2 2 23 4AC AD CD    ＝5．  4sin 5 CDBAC AC  = = ． 故选 D． 3．（2019·浙江中考模拟）如图所示， ABC△ 的顶点是正方形网格的格点，则 sin A 的值为（ ） A． 1 2 B． 5 5 C． 2 5 5 D． 10 10 【答案】B 【详解】 解：连接 CD（如图所示），设小正方形的边长为1， ∵BD=CD= 2 21 1 = 2 ，∠DBC=∠DCB=45°， ∴CD AB ， 在 Rt△ADC 中， 10AC  ， 2CD  ，则 2 5sin 510 CDA AC    ． 故选 B． 4．（2018·江西中考真题）如图，反比例函数   0ky kx   的图象与正比例函数 2y x 的图象相交于 A (1, a ), B 两点，点 C 在第四象限，CA ∥ y 轴， 90ABC   . (1)求 k 的值及点 B 的坐标； (2)求tanC 的值. 【答案】（1） 2k  ，  1, 2B   ；（2）2. 【详解】（1）∵点 A (1， a )在 2y x 上， ∴ a =2，∴ A (1， 2 )， 把 A (1， 2 )代入 ky x  得 2k  ， ∵反比例函数  0ky kx   的图象与正比例函数 2y x 的图象交于 A ， B 两点， ∴ A B、 两点关于原点O 中心对称， ∴  1 2B  ， ； （2）作 BH⊥AC 于 H，设 AC 交 x 轴于点 D， ∵ 90ABC   ， 90BHC   ，∴ C ABH  ， ∵CA ∥ y 轴，∴ BH ∥ x 轴，∴ AOD ABH  ，∴ C AOD  ， ∴ AD 2 2OD 1tanC tan AOD     . 知识点二 解直角三角形 一般地，直角三角形中，除直角外，共有五个元素，即三条边和两个锐角．由直角三角形中的已知元素， 求出其余未知元素的过程，叫做解直角三角形． 直角三角形五元素之间的关系： 1. 勾股定理（ a + b = c ） 2. ∠A+∠B=90° 3. sin A= ∠A 所对的边 斜边 = a c4. cos A= ∠A 所邻的边 斜边 = b c5. tan A= ∠A 所对的边 邻边 = a b【考查题型汇总】 考查题型七 解直角三角形的方法 1．（2018·甘肃中考模拟）如图，在 Rt△ABC 中，∠C＝90°，点 D 在 BC 边上，∠ADC＝45°，BD＝2，tanB ＝ 3 4 . (1)求 AC 和 AB 的长； (2)求 sin∠BAD 的值． 【答案】（1）AC=6，AB=10；（2）sin∠BAD= 2 10 ． 【详解】 解：（1）如图，在 Rt△ABC 中， ∵tanB＝ AC BC ＝ 3 4 ， ∴设 AC＝3x、BC＝4x， ∵BD＝2， ∴DC＝BC﹣BD＝4x﹣2， ∵∠ADC＝45°， ∴AC＝DC，即 4x﹣2＝3x， 解得：x＝2， 则 AC＝6、BC＝8， ∴AB＝ 2 2AC BC ＝10； （2）作 DE⊥AB 于点 E， 由 tanB＝ DE BE ＝ 3 4 可设 DE＝3a，则 BE＝4a， ∵DE2+BE2＝BD2，且 BD＝2， ∴（3a）2+（4a）2＝22，解得：a＝ 2 5 （负值舍去）， ∴DE＝3a＝ 6 5 ， ∵AD＝ 2 2AC DC ＝6 2 ， ∴sin∠BAD＝ DE AD ＝ 2 10 ． 2．（2018·广水市广办中心中学中考模拟）已知 Rt△ABC 中，∠C=90°，a+b=2+2 3 ，c=4，求锐角 A 的度 数． 【答案】(1)30°;(2)60°. 【解析】 将 a+b=2+2 3 两边平方，整理得 ab=4 3 ， 又因为 a+b=2+2 3 ，构造一元二次方程得 x2﹣（2+2 3 ）x+4 3 =0， 解得 x1=2，x2=2 3 则（1）sinA= 2 1 4 2  时，锐角 A 的度数是 30°， （2）sinA= 2 3 3 4 2  时，锐角 A 的度数是 60°， 所以∠A=30°或∠A=60°． 考查题型八 解斜三角形方法 1．（2019·新疆中考模拟）如图，在△ABC 中，BC＝12，tanA＝ 3 4 ，∠B＝30°；求 AC 和 AB 的长． 【答案】8+6 3 ． 【详解】 解：如图作 CH⊥AB 于 H． 在 Rt△BCH 中，∵BC＝12，∠B＝30°， ∴CH＝ 1 2 BC＝6，BH＝ 2 2BC CH ＝6 3 ， 在 Rt△ACH 中，tanA＝ 3 4 ＝ CH AH ， ∴AH＝8， ∴AC＝ 2 2AH CH ＝10， 2．（2013·湖南中考真题）如图，在△ABC 中，AD 是 BC 边上的高，AE 是 BC 边上的中线，∠C=45°，sinB= 1 3 ， AD=1． （1）求 BC 的长； （2）求 tan∠DAE 的值． 【答案】（1） 2 2 1 。 （2） 12 2  【解析】 （1）在△ABC 中，∵AD 是 BC 边上的高，∴∠ADB=∠ADC=90°。 在△ADC 中，∵∠ADC=90°，∠C=45°，AD=1，∴DC=AD=1。 在△ADB 中，∵∠ADB=90°，sinB= 1 3 ，AD=1， ∴ AD 1AB 31sinB 3    。 ∴ 2 2 2 2BD AB AD 3 1 2 2     。 ∴ BC BD DC 2 2 1    。 （2）∵AE 是 BC 边上的中线，∴CE= 1 2 BC= 12 2  。 ∴DE=CE﹣CD= 12 2  。 ∴ DE 1tan DAE 2AD 2     。 3．（2012·上海中考模拟）已知：如图，在 ABC 中， 6AB  ， 8BC  ， 60B   ．求： （1） ABC 的面积； （2） C 的余弦值． 【答案】（1）12 3 ；（2） 5 13 26 . 【解析】 （1）作 AH⊥BC，垂足为点 H． 在 Rt△ABH 中，∵∠AHB=90°，∠B=60°，AB=6， ∴BH=3，AH=3 3 ， ∴S△ABC= 1 2 ×8×3 3 =12 3 ， （2）∵BC=8，BH=3，∴CH=5． 在 Rt△ACH 中，∵AH=3 3 ，CH=5， ∴AC=2 13 ． ∴cosC= 5 5 13 262 13 CH AC   ． 考查题型九 利用解直角三角形相关知识解决视角相关问题 1．（2019·四川中考真题）2019 年，成都马拉松成为世界马拉松大满贯联盟的候选赛事，这大幅提升了成都 市的国际影响力.如图，在一场马拉松比赛中，某人在大楼 A 处，测得起点拱门 CD 的顶部C 的俯角为 35 ， 底部 D 的俯角为 45，如果 A 处离地面的高度 20AB  米，求起点拱门 CD 的高度.（结果精确到1米；参 考数据： sin35 0.57  ， cos35 0.82  ， tan35 0.70  ） 【答案】起点拱门 CD 的高度约为 6米. 【详解】 过 A 作 CD 垂线，垂足为 E，如图所示. 则四边形 DEAB 是矩形； ∴DE=AB=20 在 Rt ADE 中，∠EAD=45°，AE=DE=20 在 Rt ACE 中，CE=AE·tan35°=14， ∴CD=DE-CE=20-14=6 答：起点拱门的高度约为 6 米. 2．（2019·天津中考模拟）北京时间 2019 年 3 月 10 日 0 时 28 分，我国在西昌卫星发射中心用长征三号乙运 载火箭，成功将中星 6C 卫星发射升空，卫星进入预定轨道.如图，火星从地面C 处发射，当火箭达到 A 点 时，从位于地面雷达站 D 处测得 DA 的距离是 6km ，仰角为 42.4；1 秒后火箭到达 B 点，测得 DB的仰 角为 45.5.(参考数据：sin42.4°≈0.67，cos42.4°≈0.74，tan42.4°≈0.905，sin45.5°≈0.71，cos45.5°≈0.70， tan45.5°≈1.02) (Ⅰ)求发射台与雷达站之间的距离 CD ； (Ⅱ)求这枚火箭从 A 到 B 的平均速度是多少(结果精确到 0.01)？ 【答案】(Ⅰ)发射台与雷达站之间的距离 CD 约为 4.44km ；(Ⅱ)这枚火箭从 A 到 B 的平均速度大约是 0.51 /km s . 【详解】 (Ⅰ)在 Rt ACD 中， 6DA km ， 42.4 A CDADC cos DC AD    ， ≈0.74， ∴  6 42.4 4.44 kmCD AD cos ADC cos      . 答：发射台与雷达站之间的距离 CD 约为 4.44km . (Ⅱ)在 Rt BCD 中， 4.44km 45.5 , BCCD BDC tan BDC CD     ， ， ∴  4.44 45.5 4.44 1.02 4.5288 kmBC CD tan BDC tan        . ∵在 Rt ACD 中， ACsin ADC AD   ， ∴  6 42.4 4.02 kmAC AD sin ADC sin      . ∴  4.5288 4.02 0.5088 0.51 kmAB BC AC      . 答：这枚火箭从 A 到 B 的平均速度大约是 0.51 /km s . 3．（2019·合肥市第四十二中学中考模拟）如图，某大楼的顶部树有一块广告牌 CD，小李在山坡的坡脚 A 处测得广告牌底部 D 的仰角为 60°．沿坡面 AB 向上走到 B 处测得广告牌顶部 C 的仰角为 45°，已知山坡 AB 的坡度 i=1： 3 ，AB=10 米，AE=15 米．（i=1： 3 是指坡面的铅直高度 BH 与水平宽度 AH 的比） （1）求点 B 距水平面 AE 的高度 BH； （2）求广告牌 CD 的高度． （测角器的高度忽略不计，结果精确到 0.1 米．参考数据： 3  1.414， 1.732） 【答案】（1）点 B 距水平面 AE 的高度 BH 为 5 米. （2）宣传牌 CD 高约 2.7 米. 【详解】 解：（1）过 B 作 BG⊥DE 于 G， 在 Rt△ABF 中，i=tan∠BAH= 1 3 33  ，∴∠BAH=30° ∴BH= 1 2 AB=5（米）. 答：点 B 距水平面 AE 的高度 BH 为 5 米. （2）由（1）得：BH=5，AH=5 3 ， ∴BG=AH+AE=5 3 +15. 在 Rt△BGC 中，∠CBG=45°，∴CG=BG=5 3 +15. 在 Rt△ADE 中，∠DAE=60°，AE=15， ∴DE= 3 AE=15 3 . ∴CD=CG+GE﹣DE=5 3 +15+5﹣15 3 =20﹣10 3 ≈2.7（米）. 答：宣传牌 CD 高约 2.7 米. 4．（2019·辽宁中考模拟）如图，大楼底右侧有一障碍物，在障碍物的旁边有一幢小楼 DE，在小楼的顶端 D 处测得障碍物边缘点 C 的俯角为 30°，测得大楼顶端 A 的仰角为 45°（点 B，C，E 在同一水平直线上）.已 知 AB=80m，DE=20m，求障碍物 B，C 两点间的距离.（结果保留根号） 【答案】障碍物 B，Ｃ两点间的距离约为(60-20 3 )m. 【详解】 解： 过点 D 作 DF⊥AB 于点 F，过点 C 作 CH⊥DF 于点 H ，如图 则 DE=BF=CH=20m， 在直角三角形 ADF 中，AF=AB-DE=80-20=60m，∠ADF=45°， 所以 DF= AF=60m，CE= 0tan30 DE =20 3 m. 在直角三角形 CDE 中，DE=20m，∠DCE=30°. 所以 BC=BE-CE=(60-20 3 )m 答：障碍物 B，Ｃ两点间的距离约为(60-20 3 )m. 考查题型十 利用解直角三角形相关知识解决方向角相关问题 1．（2019·河南中考模拟）某区域平面示意图如图，点 O 在河的一侧，AC 和 BC 表示两条互相垂直的公路．甲 勘测员在 A 处测得点 O 位于北偏东 45°，乙勘测员在 B 处测得点 O 位于南偏西 73.7°，测得 AC=840m， BC=500m．请求出点 O 到 BC 的距离．参考数据：sin73.7°≈ 24 25 ，cos73.7°≈ 7 25 ，tan73.7°≈ 24 7 【答案】点 O 到 BC 的距离为 480m． 【详解】 作 OM⊥BC 于 M，ON⊥AC 于 N， 则四边形 ONCM 为矩形， ∴ON=MC，OM=NC， 设 OM=x，则 NC=x，AN=840﹣x， 在 Rt△ANO 中，∠OAN=45°， ∴ON=AN=840﹣x，则 MC=ON=840﹣x， 在 Rt△BOM 中，BM= = x， 由题意得，840﹣x+ x=500， 解得，x=480， 答：点 O 到 BC 的距离为 480m． 2．（2019·四川中考模拟）某轮船由西向东航行，在 A 处测得小岛 P 的方位是北偏东 75°，又继续航行 7 海 里后，在 B 处测得小岛 P 的方位是北偏东 60°，求此时轮船与小岛 P 的距离． 【答案】此时轮船与小岛 P 的距离是 7 海里． 【详解】 过 P 作 PD⊥AB 于点 D， ∵∠PBD＝90°﹣60°＝30° 且∠PBD＝∠PAB+∠APB，∠PAB＝90﹣75＝15° ∴∠PAB＝∠APB， ∴BP＝AB＝7（海里）． 答：此时轮船与小岛 P 的距离是 7 海里． 3．（2019·安徽中考模拟）如图，一艘轮船航行到 B 处时，测得小岛 A 在船的北偏东 60°的方向，轮船从 B 处继续向正东方向航行 20 海里到达 C 处时，测得小岛 A 在船的北偏东 30°的方向.(参考数据： 3 ≈1.732.) (1)若小岛 A 到这艘轮船航行路线 BC 的距离是 AD，求 AD 的长； (2)已知在小岛周围 17 海里内有暗礁，若轮船不改变航向继续向前行驶，试问轮船有无触礁的危险? 【答案】（1）AD≈17.32（海里）；（2）轮船不改变航向继续向前行使，轮船无触礁的危险． 【详解】 （1）如图所示． 则有∠ABD＝30°，∠ACD＝60°．∴∠CAB＝∠ABD，∴BC＝AC＝20 海里．在 Rt△ACD 中，设 CD＝x 海里， 则 AC＝2x，AD＝ 2 2 3AC CD  x，在 Rt△ABD 中，AB＝2AD＝2 3 x， BD＝ 2 2AB AD ＝3x， 又∵BD＝BC+CD， ∴3x＝20+x， ∴x＝10． ∴AD＝ 3 x＝10 3 ≈17.32（海里）； （2）∵17.32 海里＞17 海里， ∴轮船不改变航向继续向前行使，轮船无触礁的危险． 考查题型十一 利用解直角三角形相关知识解决坡角、坡度相关问题 1．（2015·湖南中考模拟）如图，河堤横断面迎水坡 AB 的坡比是 ： ，堤高 BC=10m，则坡面 AB 的长 度是（ ） A．15m B． C．20m D． 【答案】C 【解析】 试题分析：∵Rt△ABC 中，BC=10m，tanA= ： ， ∴AC=BC÷tanA= m． ∴AB= + = + = m． 故选 C． 2．（2019·湖北中考真题）如图，拦水坝的横断面为梯形 , 3ABCD AD m ，坝高 6mAE DF  ，坡角 45  ， 30   ，求 BC 的长． 【答案】 9 6 3 m 【详解】 过 A 点作 AE BC 于点 E ，过 D 作 DF BC 于点 F ， 则四边形 AEFD 是矩形，有 6, 3AE DF AD EF    ， 坡角 ,45 30    ， 6, 3 6 3BE AE CF DF     ， 6 3 6 3 9 6 3BC BE EF CF         ， (9 6 3)BC m   ， 答： BC 的长 (9 6 3)m ． 3．（2019·山东中考真题）自开展“全民健身运动”以来，喜欢户外步行健身的人越来越多，为方便群众步行 健身，某地政府决定对一段如图 1 所示的坡路进行改造．如图 2 所示，改造前的斜坡 200AB  米，坡度为 1: 3 ；将斜坡 AB 的高度 AE 降低 20AC  米后，斜坡 AB 改造为斜坡CD ，其坡度为1: 4．求斜坡 CD 的长．（结果保留根号） 【答案】斜坡 CD 的长是80 17 米． 【详解】 ∵ 90AEB  ∠ ， 200AB  ，坡度为1: 3 ， ∴ 1 3tan 33 ABE   ， ∴ 30ABE   ， ∴ 1 1002AE AB  ， ∵ 20AC  ， ∴ 80CE  ， ∵ 90CED   ，斜坡 CD 的坡度为1: 4， ∴ 1 4 CE DE  ， 即 80 1 4ED  ， 解得， 320ED  ， ∴ 2 280 320 80 17CD    米， 答：斜坡 CD 的长是80 17 米． 考查题型十二 利用解直角三角形相关知识解决高度问题 1．（2019·吉林中考模拟）在一次数学综合实践活动中，小明计划测量城门大楼的高度，在点 B 处测得楼顶 A 的仰角为 22°，他正对着城楼前进 21 米到达 C 处，再登上 3 米高的楼台 D 处，并测得此时楼顶 A 的仰角 为 45°． （1）求城门大楼的高度； （2）每逢重大节日，城门大楼管理处都要在 A，B 之间拉上绳子，并在绳子上挂一些彩旗，请你求出 A， B 之间所挂彩旗的长度（结果保留整数）．（参考数据：sin22°≈ 3 8 ，cos22°≈ 15 16 ，tan22°≈ 2 5 ） 【答案】（1）12；（2）32 米． 【详解】 解：（1）如图，作 AF⊥BC 交 BC 于点 F，交 DH 于点 E， 由题意可得，CD＝EF＝3 米，∠B＝22°，∠ADE＝45°，BC＝21 米，DE＝CF， ∵∠AED＝∠AFB＝90°， ∴∠DAE＝45°， ∴∠DAE＝∠ADE， ∴AE＝DE， 设 AF＝a 米，则 AE＝（a﹣3）米， ∵tan∠B＝ AF BF ， ∴tan22°＝ 21 ( 3) a a  ， 即 2 5 21 ( 3) a a    ， 解得，a＝12， 答：城门大楼的高度是 12 米； （2）∵∠B＝22°，AF＝12 米，sin∠B＝ ， ∴sin22°＝ 12 AB ， ∴AB≈12÷ 3 8 =32， 即 A，B 之间所挂彩旗的长度是 32 米． 2．（2015·湖南中考真题）如图 1 是“东方之星”救援打捞现场图，小红据此构造出一个如图 2 所示的数学模 型，已知：A、B、D 三点在同一水平线上，CD⊥AD，∠A=30°，∠CBD=75°，AB=60m． （1）求点 B 到 AC 的距离； （2）求线段 CD 的长度． 【答案】（1）30；（2） ͷ + ͷ ． 【解析】 (1)、过点 B 作 BE⊥AC 于点 E， 在 Rt△AEB 中，AB=60m，sinA= ，BE=ABsinA=60× =30m， (2)、cosA= ， ∴AE=60× =30 m 在 Rt△CEB 中，∠ACB=∠CBD﹣∠A=75°﹣30°=45°，∴BE=CE=30m， ∴AC=AE+CE=（30+30 ）m 在 Rt△ADC 中，sinA= ， 则 CD=（30+30 ）× =（15+15 ）m． 3．（2019·浙江中考模拟）小明想利用所学数学知识测量学校旗杆高度，如图，旗杆的顶端垂下一绳子，将 绳子拉直钉在地上，末端恰好在 C 处且与地面成 60°角，小明拿起绳子末端，后退至 E 处，拉直绳子，此时 绳子末端 D 距离地面 1.6m 且绳子与水平方向成 45°角． （1）填空：AD________AC（填“＞”，“＜”，“=”）． （2）求旗杆 AB 的高度． （参考数据： 2 ≈1.41， 3 ≈1.73，结果精确到 0.1m）． 【答案】= 【解析】 （1）由图形可得：AD=AC； （2）设绳子 AC 的长为 x 米； 在△ABC 中，AB=AC•sin60°， 过 D 作 DF⊥AB 于 F，如图： ∵∠ADF=45°， ∴△ADF 是等腰直角三角形， ∴AF=DF=x•sin45°， ∵AB﹣AF=BF=1.6，则 x•sin60°﹣x•sin45°=1.6， 解得：x=10， ∴AB=10×sin60°≈8.7（m）， 答：旗杆 AB 的高度为 8.7m． 4．（2019·天津中考模拟）如图，高楼顶部有一信号发射塔（ FM ），在矩形建筑物 ABCD 的 D C、 两点测 得该塔顶端 F 的仰角分别为 45 64.5 、 ，矩形建筑物高度 DC 为 22 米.求该信号发射塔顶端到地面的距离 FG .（精确到 1m）（参考数据：sin64.5 0.90 cos64.5 0.43   ， ，tan64.5 2.1  ） 【答案】 42FG m 【详解】 如图，作 DH FG ，设 DH x ，则CG DH x  在 FCG 中， tan64.5 2.1FG CG x    ， 在 FDH 中， FH DH x  ， 22HG FG FH    即1.1 22x  ， 解得 20x  ，  2.1 42FG x m   。 5．（2019·天津中考模拟）如图，甲、乙两座建筑物的水平距离 BC 为 78m，从甲的顶部 A 处测得乙的顶部 D 处的俯角为 49，测得底部 C 处的俯角为58 ，求甲、乙建筑物的高度 AB 和 DC (结果取整数). 参考数据： tan 49 1.15  ， tan58 1.60  . 【答案】甲建筑物的高度 AB 约为125m ，乙建筑物的高度 DC 约为 35m . 【详解】 如图，过点 D 作 DE AB ，垂足为 E . ∴ 90AED BED    . 由题意可知， 78BC  ， 49ADE   ， 58ACB  ， 90ABC   ， 90DCB   . ∴四边形 BCDE 为矩形. ∴ 78ED BC  ， DC EB . 在 Rt ABC 中， ABtan ACB BC   ， ∴ 58 78 1.60 125AB BC tan      . 在 Rt AED 中， AEtan ADE ED   ， ∴ 49AE ED tan   . ∴ 58 49 78 1.60 78 1.15 35EB AB AE BC tan ED tan             . ∴ 35DC EB  . 答：甲建筑物的高度 AB 约为125m ，乙建筑物的高度 DC 约为35m . 6．（2019·四川中考真题）如图，为了测得某建筑物的高度 AB ，在 C 处用高为 1 米的测角仪CF ，测得该 建筑物顶端 A 的仰角为 45°，再向建筑物方向前进 40 米，又测得该建筑物顶端 A 的仰角为 60°．求该建筑 物的高度 AB ．（结果保留根号） 【答案】该建筑物的高度 AB 为 (61 20 3) 米． 【详解】 解：设 AM x 米， 在 Rt AFM 中， 45AFM   ， ∴ FM AM x  ， 在 Rt AEM 中， AMtan EMAEM  ， 则 3 tan 3 AMEM xAEM   ， 由题意得， FM EM EF  ，即 3 403x x  ， 解得， 60 20 3x   ， ∴ 61 20 3AB AM MB    ， 答：该建筑物的高度 AB 为 (61 20 3) 米． 7．（2019·湖北中考真题）如图，为了测量一栋楼的高度 OE ，小明同学先在操场上 A 处放一面镜子，向后 退到 B 处，恰好在镜子中看到楼的顶部 E ；再将镜子放到C 处，然后后退到 D 处，恰好再次在镜子中看到 楼的顶部 E（O A B C D, , , , 在同一条直线上），测得 2 2.1AC m BD m ， ，如果小明眼睛距地面髙度 BF ， DG 为1.6m ，试确定楼的高度 OE ． 【答案】32 米 【详解】 设 E 关于O 的对称点为 M ，由光的反射定律知，延长GC 、 FA 相交于点 M ， 连接 GF 并延长交 OE 于点 H ， / /GF ACQ ， MAC MFG ∽ ， AC MA MO= =FG MF MH  ， 即： AC OE OE OE= = =BD MH MO+OH OE+BF ， 2 1.6 2.1 OE OE   ， 32OE  ， 答：楼的高度 OE 为 32 米．