初中数学中考总复习课件PPT：第19课时　全等三角形 20页

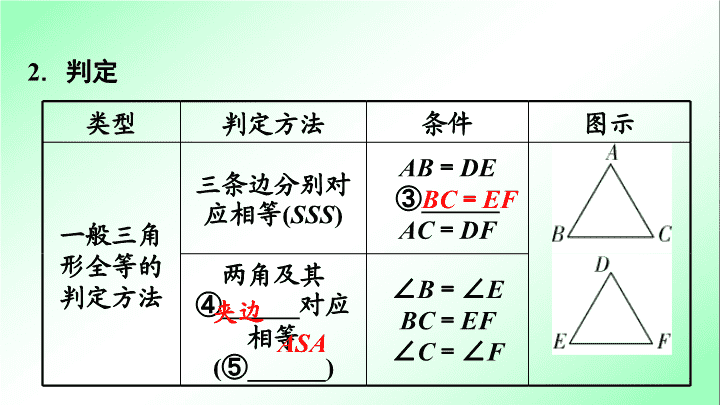
第一部分 夯实基础　提分多 第 三 单元 函数 第 19 课时　全等三角形 1 ． 概念 ：能够完全重合的两个三角形叫做全等三角形． 2 ． 性质 (1) 全等三角形的对应边① ______ ，对应角② ______ ； (2) 全等三角形的对应线段 ( 角平分线、中线、高线、中位线 ) 相等、周长相等、面积相等． 基础点 1 全等三角形的性质及判定 相等 相等 基础点巧练妙记 2 ． 判定 类型 判定方法 条件 图示 一般三角形全等的判定方法 三条边分别对应相等 ( SSS ) AB ＝ DE ③______ 　　　 AC ＝ DF 两角及其④ ______ 对应相等 (⑤______) ∠ B ＝∠ E BC ＝ EF ∠ C ＝∠ F BC ＝ EF 夹边 ASA 类型 判定方法 条件 图示 一般三角形全等的判定方法 两角及其一角所对的边对应相等 ( AAS ) ⑥______ 　　　∠ C ＝∠ F AC ＝ DF 两边及其⑦ ________ 对应相等 (⑧______) AB ＝ DE ∠ A ＝∠ D AC ＝ DF 夹角 ∠ B ＝∠ E SAS 类型 判定方法 条件 图示 直角三角形全等的判定方法（注：一般三角形全等的判定方法也适用于直角三角形） 一条直角边和⑨ ______ 分别对应相等 (⑩_____) ⑪______ _________ 　　　 AC ＝ DF 斜边 HL AB ＝ DE ( 或 BC ＝ EF ) 4 ． 三角形全等的判定思路 证三角形全等 已知两边 已知一边 和一角 已知两角 找夹边→ ASA 找任一边→ AAS 找夹角→ SAS 找直角→ HL 找夹角→ SSS 边为角的对边→找任一边→ AAS 边为角的邻边→ 找夹角的另一边→ SAS 找夹角的另一角→ ASA 找边的对角→ AAS 5 ． 全等三角形常见模型 模型 图形示例 平移模型 模型 图形示例 对称模型 模型 图形示例 旋转模型 注 ：若 AC ＝ BC ， CD ＝ CE ，∠ ACB ＝∠ DCE ，则此模型也叫手拉手模型 模型 图形示例 平移 + 旋转模型 角平分线模型 模型 图形示例 三垂直模型 重难点精讲优练 类型 1 全等三角形的相关证明与计算 练习 1 　 如图，已知 AC ⊥ BC ， BD ⊥ AD ， AC 与 BD 交于点 O ， AC ＝ BD . 求证：△ ABC ≌ △ BAD . 练习 1 题图 证明 ： ∵ AC ⊥ BC ， BD ⊥ AD ， ∴∠ C ＝∠ D ＝ 90° ， 在 Rt △ ABC 和 Rt △ BAD 中， AB ＝ BA AC ＝ BD ， ∴△ ABC ≌ △ BAD ( HL ) ． 练习 2 　 如图，已知 AB ， CD 相交于点 O ， AD ＝ CB ， AB ＝ CD. 求证：∠ B ＝∠ D . 练习 2 题图 证明 ：如解图，连接 AC ，在△ ABC 和△ CDA 中， AB ＝ CD CB ＝ AD AC ＝ CA ， ∴△ ABC ≌ △ CDA ( SSS ) ，∴∠ B ＝∠ D . 练习 2 题解图 练习 3 　 如图，△ ADE 与△ CBF 的边 AE 、 CF 在同一条直线上， DE ∥ BF ， AD ∥ BC ， AF ＝ CE . 求证：△ ADE ≌ △ CBF . 练习 3 题图 证明 ：∵ DE ∥ BF ， AD ∥ BC ， ∴∠ DEA ＝∠ BFC ，∠ A ＝∠ C ， ∵ AF ＝ CE ，∴ AF ＋ FE ＝ FE ＋ CE ，即 AE ＝ CF ，在△ ADE 和△ CBF 中， ∠ DEA ＝∠ BFC AE ＝ CF ∠ A ＝∠ C ， ∴△ ADE ≌ △ CBF ( ASA ) ． 练习 4 　 如图，已知 AB ⊥ AC ， AB ＝ AC ， DE 经过点 A ，且 CD ⊥ DE ， BE ⊥ DE ，垂足分别为点 D ， E . 求证：△ ADC ≌ △ BEA . 练习 4 题图 证明 ： ∵ AB ⊥ AC ， CD ⊥ DE ， BE ⊥ DE ， ∴∠ BAC ＝∠ D ＝∠ E ＝ 90° ，∴∠ CAD ＋∠ EAB ＝ 90° ，∠ DCA ＋∠ CAD ＝ 90° ， ∴∠ DCA ＝∠ EAB ，在△ ADC 和△ BEA 中， ∠ D ＝∠ E ∠ DCA ＝∠ EAB AC ＝ BA ∴△ ADC ≌△ BEA ( AAS ) ． 练习 4 题图 练习 5 　 如图，在△ PAB 中， PA ＝ PB ， M ， N ， K 分别是 PA ， PB ， AB 上的点，且 AM ＝ BK ， BN ＝ AK ，若∠ MKN ＝ 42 ° ，求∠ P 的度数． 练习 5 题图 解 ：∵ PA ＝ PB ，∴∠ A ＝∠ B ， 在△ AMK 和△ BKN 中， AM ＝ BK ∠ A ＝∠ B AK ＝ BN ， ∴△ AMK ≌ △ BKN ( SAS ) ，∴∠ AMK ＝∠ BKN ，∵∠ MKB ＝∠ MKN ＋∠ NKB ＝∠ A ＋∠ AMK ， ∴∠ A ＝∠ MKN ＝ 42° ，∴∠ P ＝ 180° －∠ A －∠ B ＝ 96°.