人教版9年级上册数学全册导学案22_9 二次函数导学案 4页

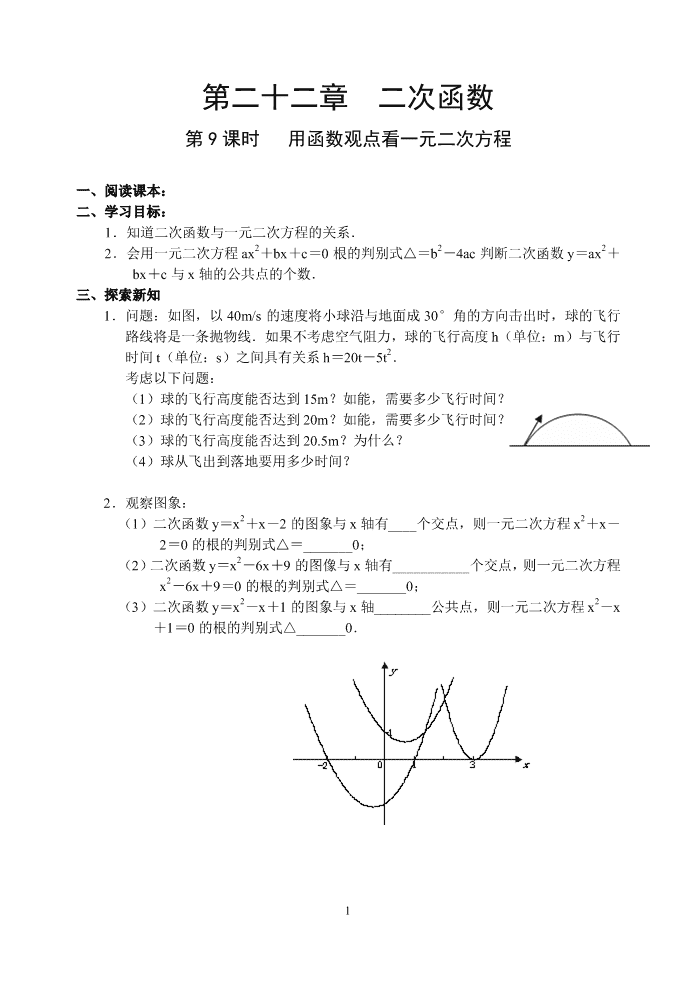
1 第二十二章 二次函数 第 9 课时 用函数观点看一元二次方程 一、阅读课本： 二、学习目标： 1．知道二次函数与一元二次方程的关系． 2．会用一元二次方程 ax2＋bx＋c＝0 根的判别式△＝b2－4ac 判断二次函数 y＝ax2＋ bx＋c 与 x 轴的公共点的个数． 三、探索新知 1．问题：如图，以 40m/s 的速度将小球沿与地面成 30°角的方向击出时，球的飞行 路线将是一条抛物线．如果不考虑空气阻力，球的飞行高度 h（单位：m）与飞行 时间 t（单位：s）之间具有关系 h＝20t－5t2． 考虑以下问题： （1）球的飞行高度能否达到 15m？如能，需要多少飞行时间？ （2）球的飞行高度能否达到 20m？如能，需要多少飞行时间？ （3）球的飞行高度能否达到 20.5m？为什么？ （4）球从飞出到落地要用多少时间？ 2．观察图象： （1）二次函数 y＝x2＋x－2 的图象与 x 轴有____个交点，则一元二次方程 x2＋x－ 2＝0 的根的判别式△＝_______0； （2）二次函数 y＝x2－6x＋9 的图像与 x 轴有___________个交点，则一元二次方程 x2－6x＋9＝0 的根的判别式△＝_______0； （3）二次函数 y＝x2－x＋1 的图象与 x 轴________公共点，则一元二次方程 x2－x ＋1＝0 的根的判别式△_______0． 2 四、理一理知识 1．已知二次函数 y＝－x2＋4x 的函数值为 3，求自变量 x 的值，可以看作解一元二次 方程 __________________．反之，解一元二次方程－x2＋4x＝3 又可以看作已知二次函 数 __________________的函数值为 3 的自变量 x 的值． 一般地：已知二次函数 y＝ax2＋bx＋c 的函数值为 m，求自变量 x 的值，可以看作 解一元二次方程 ax2＋bx＋c＝m．反之，解一元二次方程 ax2＋bx＋c＝m 又可以看 作已知二次函数 y＝ax2＋bx＋c 的值为 m 的自变量 x 的值． 2．二次函数 y＝ax2＋bx＋c 与 x 轴的位置关系： 一元二次方程 ax2＋bx＋c＝0 的根的判别式△＝b2－4ac． （1）当△＝b2－4ac＞0 时 抛物线 y＝ax2＋bx＋c 与 x 轴有两个交点； （2）当△＝b2－4ac＝0 时 抛物线 y＝ax2＋bx＋c 与 x 轴只有一个交点； （3）当△＝b2－4ac＜0 时 抛物线 y＝ax2＋bx＋c 与 x 轴没有公共点． 五、基本知识练习 1．二次函数 y＝x2－3x＋2，当 x＝1 时，y＝________；当 y＝0 时，x＝_______． 2．二次函数 y＝x2－4x＋6，当 x＝________时，y＝3． 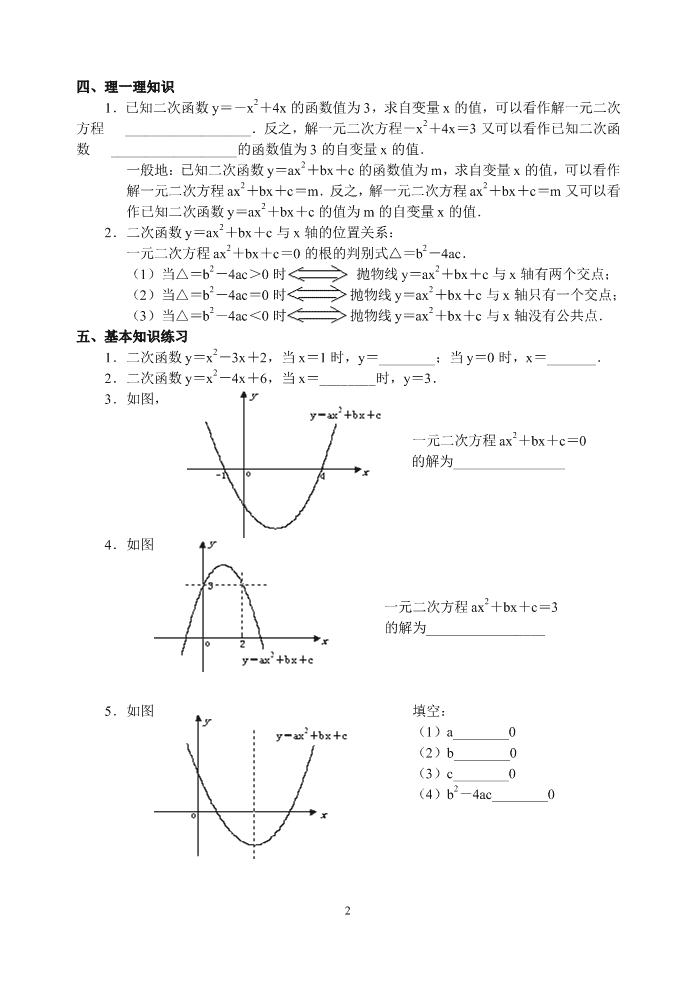3．如图， 一元二次方程 ax2＋bx＋c＝0 的解为________________ 4．如图 一元二次方程 ax2＋bx＋c＝3 的解为_________________ 5．如图 填空： （1）a________0 （2）b________0 （3）c________0 （4）b2－4ac________0 3 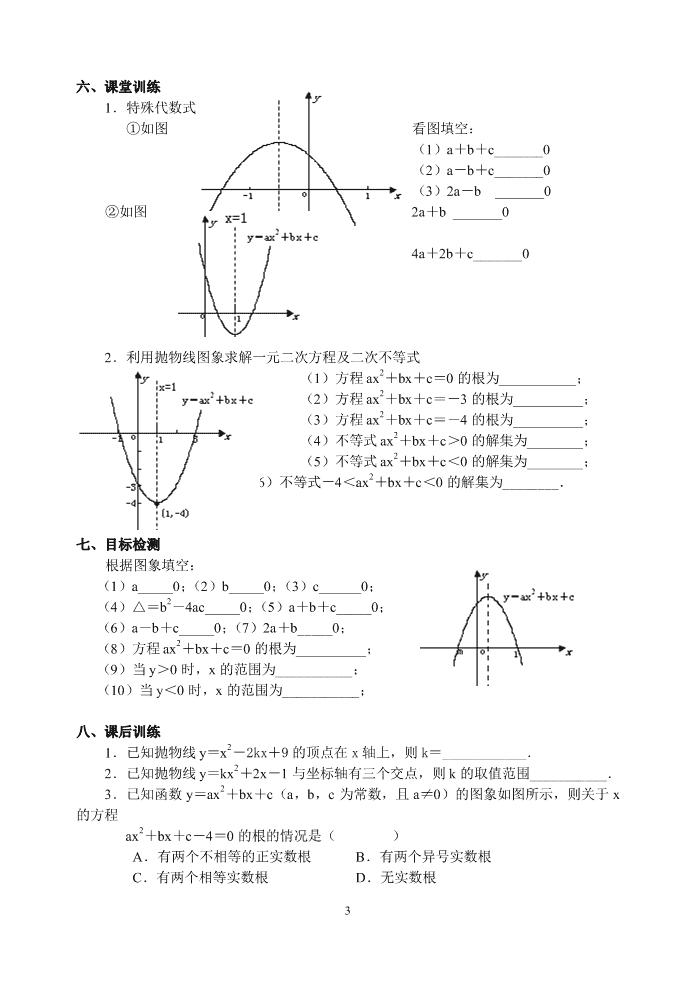六、课堂训练 1．特殊代数式求值： ①如图 看图填空： （1）a＋b＋c_______0 （2）a－b＋c_______0 （3）2a－b _______0 ②如图 2a＋b _______0 4a＋2b＋c_______0 2．利用抛物线图象求解一元二次方程及二次不等式 （1）方程 ax2＋bx＋c＝0 的根为___________； （2）方程 ax2＋bx＋c＝－3 的根为__________； （3）方程 ax2＋bx＋c＝－4 的根为__________； （4）不等式 ax2＋bx＋c＞0 的解集为________； （5）不等式 ax2＋bx＋c＜0 的解集为________； （6）不等式－4＜ax2＋bx＋c＜0 的解集为________． 七、目标检测 根据图象填空： （1）a_____0；（ 2）b_____0；（ 3）c______0； （4）△＝b2－4ac_____0；（ 5）a＋b＋c_____0； （6）a－b＋c_____0；（ 7）2a＋b_____0； （8）方程 ax2＋bx＋c＝0 的根为__________； （9）当 y＞0 时，x 的范围为___________； （10）当 y＜0 时，x 的范围为___________； 八、课后训练 1．已知抛物线 y＝x2－2kx＋9 的顶点在 x 轴上，则 k＝____________． 2．已知抛物线 y＝kx2＋2x－1 与坐标轴有三个交点，则 k 的取值范围___________． 3．已知函数 y＝ax2＋bx＋c（a，b，c 为常数，且 a≠0）的图象如图所示，则关于 x 的方程 ax2＋bx＋c－4＝0 的根的情况是（ ） A．有两个不相等的正实数根 B．有两个异号实数根 C．有两个相等实数根 D．无实数根 4 4．如图为二次函数 y＝ax2＋bx＋c 的图象，在下列说法中： ①ac＜0；②方程 ax2＋bx＋c＝0 的根是 x1＝－1，x2＝3；③a＋b＋c＞0； ④当 x＞1 时，y 随 x 的增大而增大． 正确的说法有__________________（把正确的序号都填在横线上）．