2019九年级数学上册 第二十四章 24正多边形和圆 4页

第二十四章 24.3正多边形和圆 知识点1：正多边形与圆的关系 ‎ ‎(1)各边相等,各角也相等的多边形叫做正多边形.‎ ‎(2)将一个圆n(n≥3)等分,顺次连接各个等分点得到的多边形是正n边形,这个正n边形叫做圆的内接多边形,这个圆叫做正n边形的外接圆.‎ 关键提醒:(1)根据定义,判断一个多边形是否是正多边形,必须满足两个条件:各边相等,各角相等.缺一不可,如菱形的各边相等,矩形的各角都相等,但它们都不是正多边形.‎ ‎(2)要判定一个多边形是不是正多边形,除了根据定义来判定外,还可以根据正多边形与圆的关系来判定,即依次连接圆的n(n≥3)等分点,所得的多边形是正n多边形.‎ ‎(3)把圆分成n(n≥3)等分,经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形.‎ ‎(4)任意三角形都具有内切圆和外接圆,但只有正三角形的外接圆和内切圆才是同心圆.任意多边形不一定具有外接圆和内切圆,但正多边形一定有外接圆和内切圆,并且是同心圆.‎ 知识点2：正多边形的有关概念与计算 ‎ 正多边形的中心:正多边形外接圆的圆心叫做正多边形的中心;‎ 正多边形的半径:正多边形外接圆的半径叫做正多边形的半径;‎ 正多边形的中心角:正多边形每一条边所对的圆心角叫做正多边形的中心角;‎ 正多边形的边心距:正多边形的中心到一边的距离叫做正多边形的边心距;‎ 正多边形的对称性:‎ ‎①正多边形的轴对称性:正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过正n边形的中心;‎ ‎②正多边形的中心对称性:边数为偶数的正多边形是中心对称图形,它的中心是对称中心;‎ ‎③正多边形的旋转对称性:正多边形都是旋转对称图形,最小的旋转角等于中心角.‎ 关键提醒:(1)正多边形的有关概念是针对圆而言的,比如正多边形的中心角相对于圆而言就应叫做圆心角;‎ ‎(2)边心距与弦心距的区别与联系:边心距是圆心到正多边形一边的距离,此时的边心距也可以看作是正多边形的外接圆中,圆心到弦的距离;‎ 4‎ ‎(3)正多边形的有关计算:‎ ‎①正n边形的每个内角为 ;②正n边形的每个中心角为;③正多边形的外角;④设正n边形的边长、边心距、周长、面积分别为an,rn,ln,Sn,则ln=nan,Sn=rnln;‎ ‎(4) 有关正多边形的计算,常添加辅助线:边心距、半径与边长的一半构造直角三角形求解相关边或角.‎ 知识点3：正多边形的画法 ‎ 画正多边形的方法——一般通过等分圆周的方法:用量角器等分圆周或用尺规等分圆周.‎ 关键提醒:(1)用量角器等分圆周有两种方法:一是通过依次作相等的圆心角来等分圆周;另一种方法是先用量角器画一个的圆心角,然后在圆上依次截取与这个圆心角所对弧相等的弧,得到n个等分点;‎ ‎(2)用尺规等分圆周的方法:对于正四边形及其2n(n为自然数)倍边形(如正八边形、正十六边形…)、正六边形及其2n(n为自然数)倍边形(如正十二边形、正二十四边形…)和正三角形等特殊图形可以用直尺和圆规等分圆周.‎ 考点1：关于正多边形的边长、边心距、半径的计算问题 ‎【例1】  若正六边形的边长为250px,则它的边心距为(　　).‎ A. cm　　　B. 125px　　　C. ‎5cm　　　D. 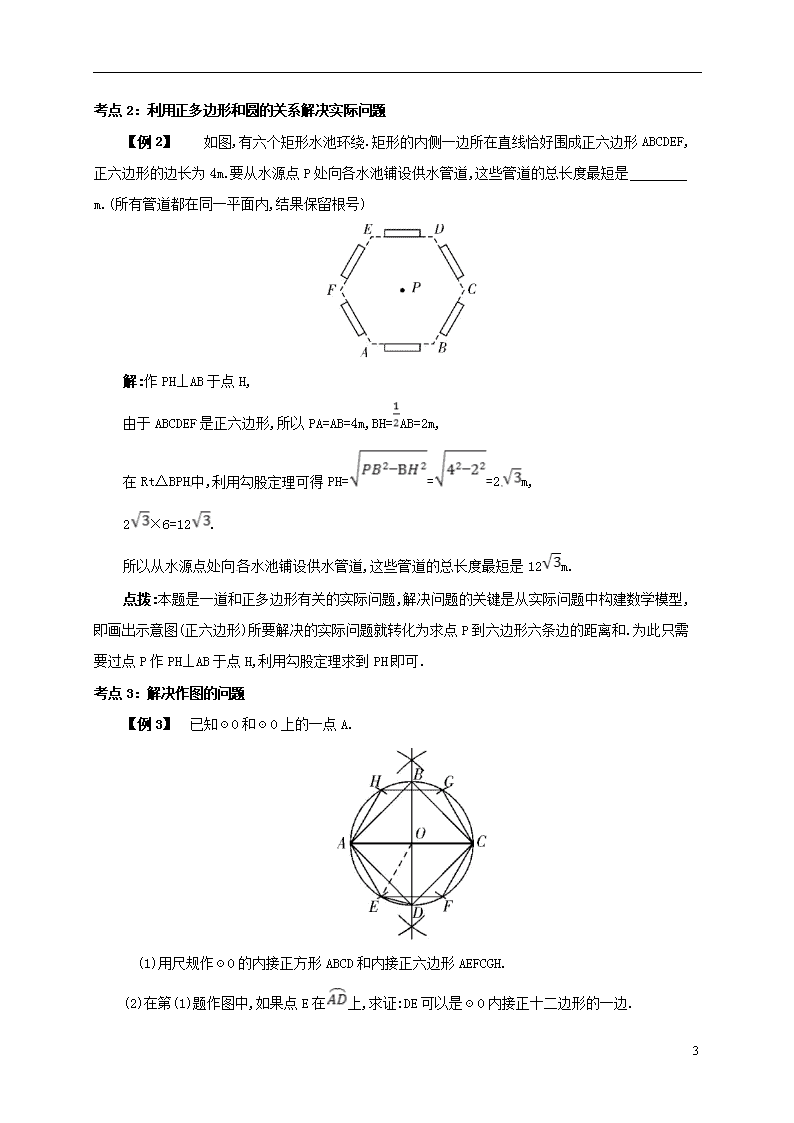250px 答案:C.‎ 点拨:如图,正六边形的中心角为60°,因此∠AOG=30°,求边心距OG可转化到Rt△AOG中去解决.AG=125px,AO=2AG=250px,所以OG==5(cm).‎ 4‎ 考点2：利用正多边形和圆的关系解决实际问题 ‎【例2】  如图,有六个矩形水池环绕.矩形的内侧一边所在直线恰好围成正六边形ABCDEF,正六边形的边长为‎4m.要从水源点P处向各水池铺设供水管道,这些管道的总长度最短是　　　　m.(所有管道都在同一平面内,结果保留根号)‎ ‎               ‎ 解:作PH⊥AB于点H,‎ 由于ABCDEF是正六边形,所以PA=AB=‎4m,BH=AB=‎2m,‎ 在Rt△BPH中,利用勾股定理可得PH===2m,‎ ‎2×6=12.‎ 所以从水源点处向各水池铺设供水管道,这些管道的总长度最短是12m.‎ 点拨:本题是一道和正多边形有关的实际问题,解决问题的关键是从实际问题中构建数学模型,即画出示意图(正六边形)所要解决的实际问题就转化为求点P到六边形六条边的距离和.为此只需要过点P作PH⊥AB于点H,利用勾股定理求到PH即可.‎ 考点3：解决作图的问题 ‎【例3】 已知☉O和☉O上的一点A.‎ ‎ (1)用尺规作☉O的内接正方形ABCD和内接正六边形AEFCGH.‎ ‎(2)在第(1)题作图中,如果点E在上,求证:DE可以是☉O内接正十二边形的一边.‎ 4‎ 解:(1)①作直径AC;‎ ‎②用尺规作直径BD⊥AC(作图痕迹如图24.3-3所示,过程略),依次连接AB、BC、CD、DA,则四边形ABCD为☉O的内接正方形;‎ ‎③分别以A、C为圆心,OA为半径画弧,交☉O于点E、H、F、G,顺次连接AE、EF、FC、CG、GH、HA,则六边形AEFCGH为☉O的内接正六边形(如图).‎ ‎(2)连接OE.‎ ‎∵　∠AOD==90°,∠AOE==60°,‎ ‎∴　∠DOE=∠AOD-∠AOE=90°-60°=30°.‎ ‎∵　正十二边形的中心角为30°,‎ ‎∴　DE可以是☉O内接正十二边形的一边.‎ 点拨:(1)可以通过作相互垂直的直径,获得90°的圆心角来作圆的内接正方形.因为等于半径的弦所对的圆心角为60°,因此不难作出☉O的内接正六边形;(2)证明DE可以是☉O内接正十二边形的一边,只要证明DE所对的圆心角等于=30°即可.‎ ‎ ‎ 4‎