2011年山东省青岛市中考数学真题 8页

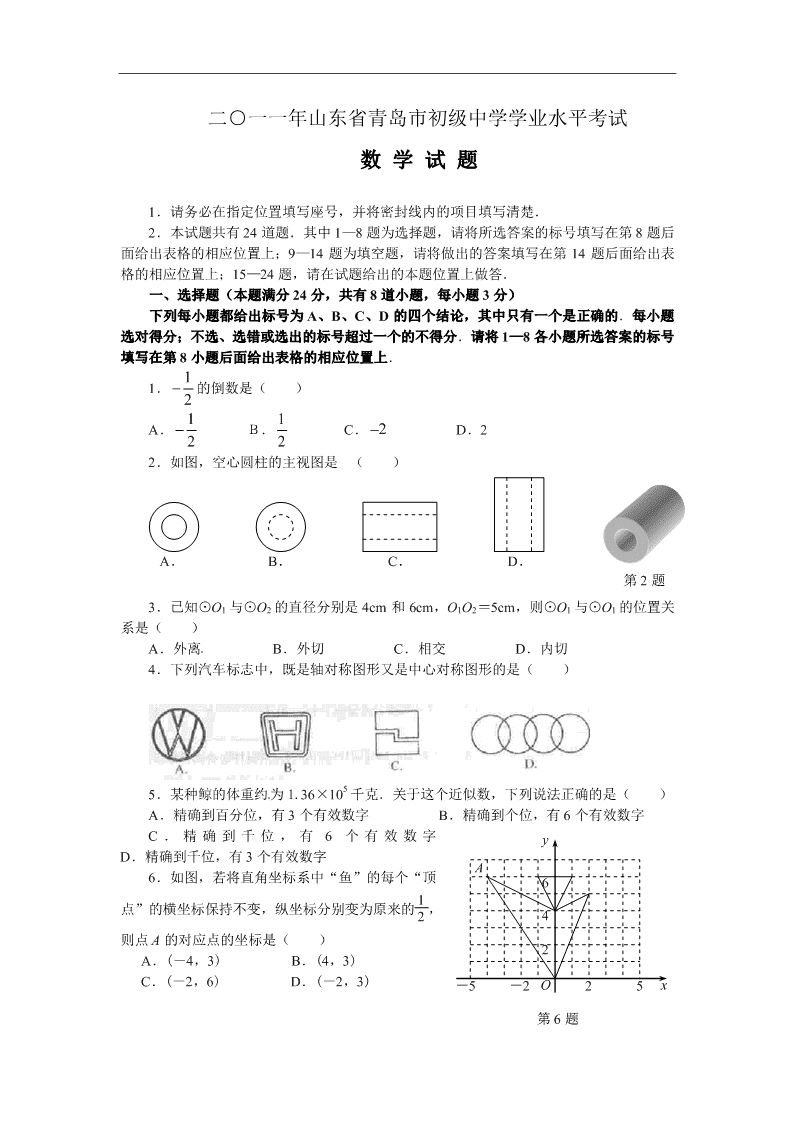
二○一一年山东省青岛市初级中学学业水平考试 数 学 试 题 1．请务必在指定位置填写座号，并将密封线内的项目填写清楚． 2．本试题共有 24 道题．其中 1—8 题为选择题，请将所选答案的标号填写在第 8 题后 面给出表格的相应位置上；9—14 题为填空题，请将做出的答案填写在第 14 题后面给出表 格的相应位置上；15—24 题，请在试题给出的本题位置上做答． 一、选择题（本题满分 24 分，共有 8 道小题，每小题 3 分） 下列每小题都给出标号为 A、B、C、D 的四个结论，其中只有一个是正确的．每小题 选对得分；不选、选错或选出的标号超过一个的不得分．请将 1—8 各小题所选答案的标号 填写在第 8 小题后面给出表格的相应位置上． 1． 1 2 的倒数是（ ） A． Ｂ． 1 2 C． 2 D．2 2．如图，空心圆柱的主视图是 （ ） 3．已知⊙O1 与⊙O2 的直径分别是 4cm 和 6cm，O1O2＝5cm，则⊙O1 与⊙O1 的位置关 系是（ ） A．外离 B．外切 C．相交 D．内切 4．下列汽车标志中，既是轴对称图形又是中心对称图形的是（ ） 5．某种鲸的体重约为 1.36×105 千克．关于这个近似数，下列说法正确的是（ ） A．精确到百分位，有 3 个有效数字 B．精确到个位，有 6 个有效数字 C ．精确到千位，有 6 个 有 效 数 字 D．精确到千位，有 3 个有效数字 6．如图，若将直角坐标系中“鱼”的每个“顶 点”的横坐标保持不变，纵坐标分别变为原来的 1 2 ， 则点 A 的对应点的坐标是（ ） A．(－4，3) B．(4，3) C．(－2，6) D．(－2，3) A． B． C． D． 第 2 题 O A y x 6 4 2 2 5 －5 －2 第 6 题 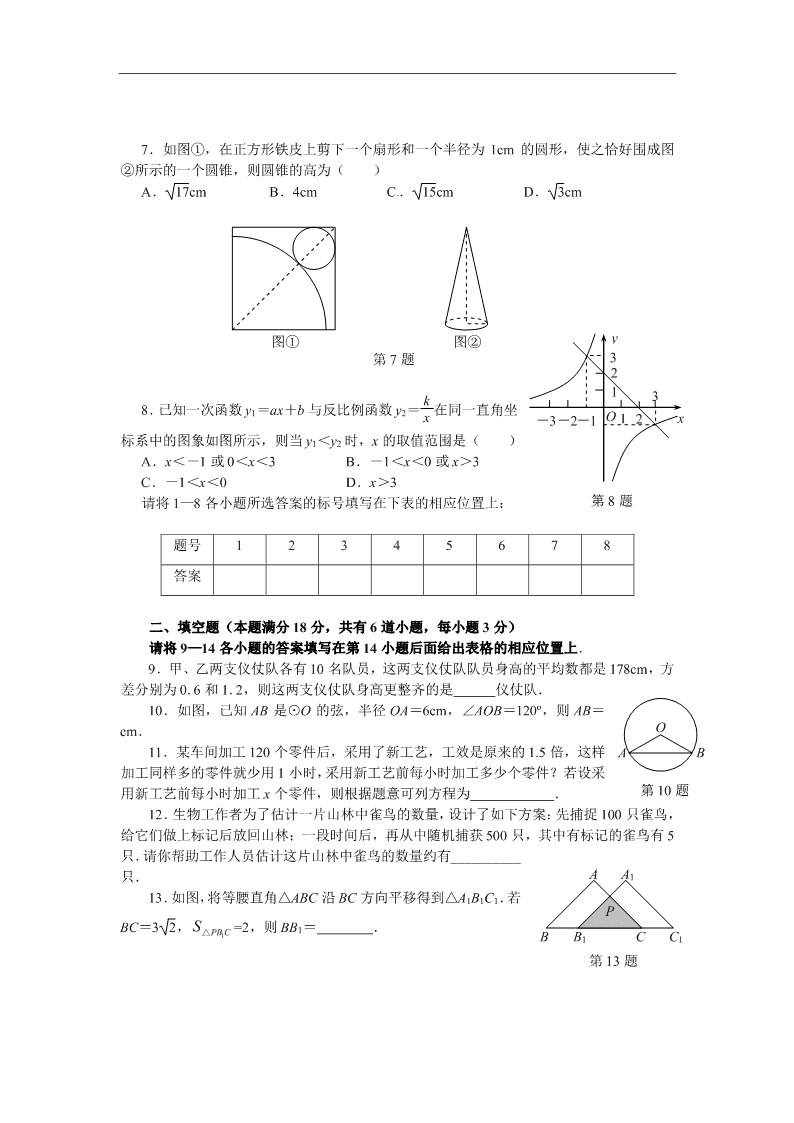7．如图①，在正方形铁皮上剪下一个扇形和一个半径为 1cm 的圆形，使之恰好围成图 ②所示的一个圆锥，则圆锥的高为（ ） A． 17cm B．4cm C． 15cm D． 3cm 8．已知一次函数 y1＝ax＋b 与反比例函数 y2＝ k x 在同一直角坐 标系中的图象如图所示，则当 y1＜y2 时，x 的取值范围是（ ） A．x＜－1 或 0＜x＜3 B．－1＜x＜0 或 x＞3 C．－1＜x＜0 D．x＞3 请将 1—8 各小题所选答案的标号填写在下表的相应位置上： 题号 1 2 3 4 5 6 7 8 答案 二、填空题（本题满分 18 分，共有 6 道小题，每小题 3 分） 请将 9—14 各小题的答案填写在第 14 小题后面给出表格的相应位置上． 9．甲、乙两支仪仗队各有 10 名队员，这两支仪仗队队员身高的平均数都是 178cm，方 差分别为 0.6 和 1.2，则这两支仪仗队身高更整齐的是 仪仗队． 10．如图，已知 AB 是⊙O 的弦，半径 OA＝6cm，∠AOB＝120º，则 AB＝ cm． 11．某车间加工 120 个零件后，采用了新工艺，工效是原来的 1.5 倍，这样 加工同样多的零件就少用 1 小时，采用新工艺前每小时加工多少个零件？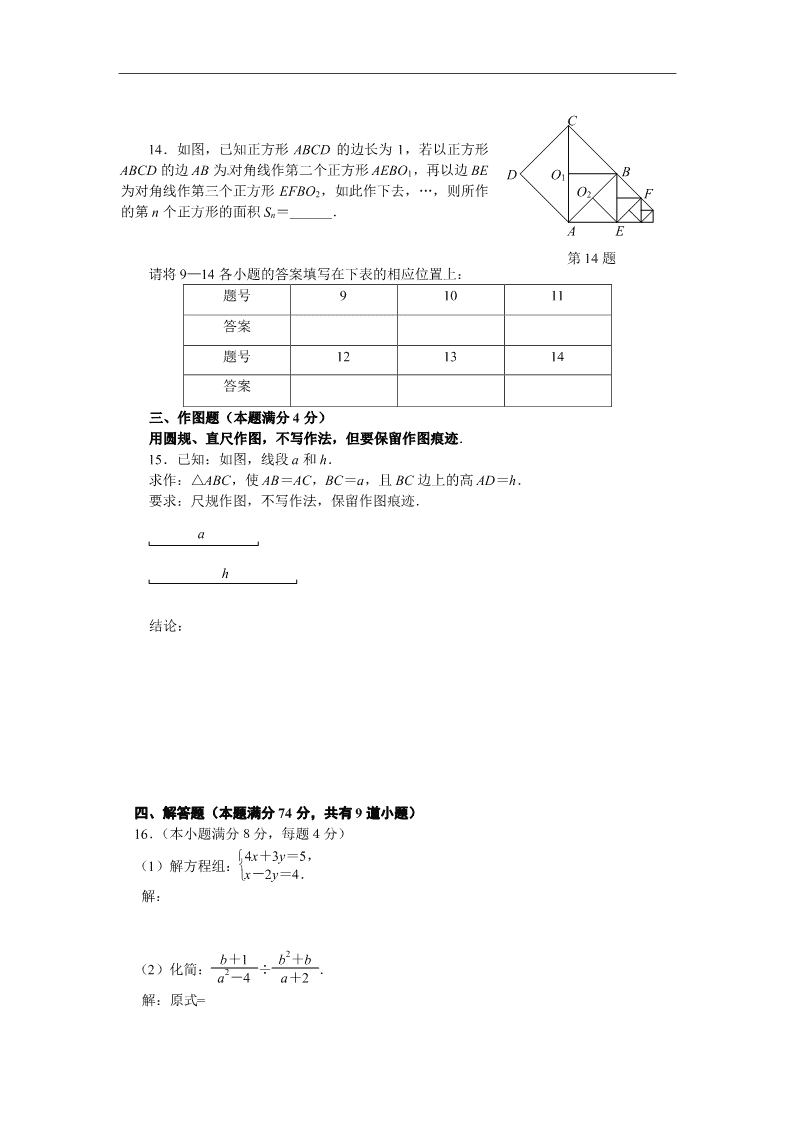若设采 用新工艺前每小时加工 x 个零件，则根据题意可列方程为 ． 12．生物工作者为了估计一片山林中雀鸟的数量，设计了如下方案：先捕捉 100 只雀鸟， 给它们做上标记后放回山林；一段时间后，再从中随机捕获 500 只，其中有标记的雀鸟有 5 只．请你帮助工作人员估计这片山林中雀鸟的数量约有__________ 只． 13．如图，将等腰直角△ABC 沿 BC 方向平移得到△A1B1C1．若 BC＝3 2， 1PB CS△ =2，则 BB1＝ ． 图① 图② 第 7 题 A B O 第 10 题 第 13 题 A A1 B B1 C C1 P y O x 3 －1 3 第 8 题 2 1 －2 －3 1 2 14．如图，已知正方形 ABCD 的边长为 1，若以正方形 ABCD 的边 AB 为对角线作第二个正方形 AEBO1，再以边 BE 为对角线作第三个正方形 EFBO2，如此作下去，…，则所作 的第 n 个正方形的面积 Sn＝ ． 请将 9—14 各小题的答案填写在下表的相应位置上： 题号 9 10 11 答案 题号 12 13 14 答案 三、作图题（本题满分 4 分） 用圆规、直尺作图，不写作法，但要保留作图痕迹． 15．已知：如图，线段 a 和 h． 求作：△ABC，使 AB＝AC，BC＝a，且 BC 边上的高 AD＝h． 要求：尺规作图，不写作法，保留作图痕迹． 结论： 四、解答题（本题满分 74 分，共有 9 道小题） 16．（本小题满分８分，每题４分） （1）解方程组：  4x＋3y＝5， x－2y＝4． 解： （2）化简： b＋1 a2－4 ÷ b2＋b a＋2 ． 解：原式= a h A B C D E F O1 O2 第 14 题 17．(本小题满分 6 分) 图①是某城市三月份 1 至 8 日的日最高气温随时间变化的折线统计图，小刚根据图①将 数据统计整理后制成图②． 根据图中的信息解答下列问题： (1)在图②中补全条形统计图； (2)这 8 天的日最高气温的中位数是 ºC； (3)计算这 8 天的日最高气温的平均数． 解：（3） 18．(本小题满分 6 分) 小明和小亮用图中的转盘做游戏：分别转动转盘两次，若两次数字之差(大数减小数) 大于或等于 2，小明得 1分，否则小亮得 1 分．你认为游戏是否公平？请说明理由.若不公平， 请你修改规则，使游戏对双方公平． 解： 温度（ºC） 日期 O 1 2 3 4 5 6 7 8 1 2 5 3 4 图① 天数/天 温度（ºC） 1 2 3 4 0 1 2 3 4 图② 第 17 题 1 2 4 第 18 题 3 19．(本小题满分 6 分) 某商场准备改善原有楼梯的安全性能，把倾斜角由原来的 40º减至 35º．已知原楼梯 AB 长为 5m，调整后的楼梯所占地面 CD 有多长？（结果精确到 0.1m） (参考数据：sin40º≈0.64，cos40º≈0.77，sin35º≈0.57，tan35º≈0.70) 解： 20．(本小题满分８分) 某企业为了改善污水处理条件 ，决定购买 A、B 两种型号的污水处理设备共 8 台，其中每台的价格、 月处理污水量如下表： 经预算，企业最多支出 57 万元购买污水处理设 备，且要求设备月处理污水量不低于 1490 吨． (1)企业有哪几种购买方案？ (2)哪种购买方案更省钱？ 解：（1） （2） A 型 B 型 价格(万元/台) 8 6 月处理污水量(吨/月) 200 180 40º 35º A D B C 第 19 题 21．(本小题满分８分) 已知：□ABCD 中，E、F 分别是 AB、CD 的中点，连接 AF、CE． （1）求证：△BEC≌△DFA； （2）连接 AC，当 CA＝CB 时，判断四边形 AECF 是什么特殊四边形？并证明你的结 论． 证明：（1） （2） 22．(本小题满分 10 分) 某商场经营某种品牌的童装，购进时的单价是 60 元．根据市场调查，在一段时间内， 销售单价是 80 元时，销售量是 200 件，而销售单价每降低 1 元，就可多售出 20 件． （1）写出销售量 y（件）与销售单价 x（元）之间的函数关系式； （2）写出销售该品牌童装获得的利润 w（元）与销售单价 x（元）之间的函数关系式； （3）若童装厂规定该品牌童装销售单价不低于 76 元，且商场要完成不少于 240 件的销 售任务，则商场销售该品牌童装获得的最大利润是多少元？ 解：（1） （2） （3） A E B C F D 第 21 题 a a a a b b b b 图① 23．(本小题满分 10 分) 问题提出 我们在分析解决某些数学问题时，经常要比较两个数或代数式的大小．而解决问题的策 略一般要进行一定的转化，其中“作差法”就是常用方法之一．所谓“作差法”：就是 通过作差、变形，并利用差的符号来确定他们的大小，即要比较代数式 M、N 的大小， 只要作出它们的差 M－N，若 M－N＞0，则 M＞N；若 M－N＝0，则 M＝N；若 M－N ＜0，则 M＜N． 问题解决 如图①，把边长为 a＋b(a≠b)的大正方形分割成两个边长分别是 a、b的小正方形及两 个矩形，试比较两个小正方形的面积之和 M 与两个矩形面积之和 N 的大小． 解：由图可知，M＝a2＋b2，N＝2ab． ∴M－N＝a2＋b2－2ab＝(a－b)2． ∵a≠b，∴(a－b)2＞0． ∴M－N＞0． ∴M＞N． 类比应用 (1)已知小丽和小颖购买同一种商品的平均价格分别为 a＋b 2 元/千克、 2ab a＋b 元/千克 (a、b 是正数，且 a≠b)，试比较小丽和小颖所购买商品的平均价格的高低． 解： （2）试比较图②、图③两个矩形的周长 M1、N1 的大小(b＞c)． 解： 图③ a＋b b＋3c b＋c a－c 图② P B Q A M D C F 第 24 题 联系拓广 小刚在超市里买了一些物品，用一个长方体的箱子“打包”，箱子的尺寸如图④所示(b ＞a＞c＞0)，售货员分别可按图⑤、图⑥、图⑦三种方法进行捆绑，吻哪种方法用绳最 短？哪种方法用绳最长？请说明理由． 解： 24．(本小题满分 12 分) 已知，如图在△ABC 中，AB＝AC＝10cm，BD⊥AC 于 D，且 BD＝8cm．点 M 从点 A 出发，沿 AC 方向匀速运动，速度为 2cm/s；同时，直线 PQ 由点 B 出发沿 BA 的方向匀速 运动，速度为 1cm/s，运动过程中始终保持 PQ∥AC，直线 PQ 交 AB 于 P、交 BC 于 Q、交 BD 于 F．连接 PM，设运动时间为 t（s）(0＜t＜5)．解答下列问题： （1）当 t 为何值时，四边形 PQCM 是平行四边形？ （2）设四边形 PQCM 的面积为 y（cm）2，求 y 与 t 之间的函数关系式； （3）是否存在某一时刻 t，使 S 四边形 PQCM＝ 9 16 S△ABC？若存在，求出 t 的值；若不存在， 说明理由； （4）连接 PC，是否存在某一时刻 t，使点 M 在线段 PC 的垂直平分线上？若存在，求 出此时 t 的值；若不存在，说明理由． 解：（1） （2） 图④ 图⑤ 图⑥ 图⑦ a b c