人教版九年级数学上册第二十三章 旋转 单元测试题 24页

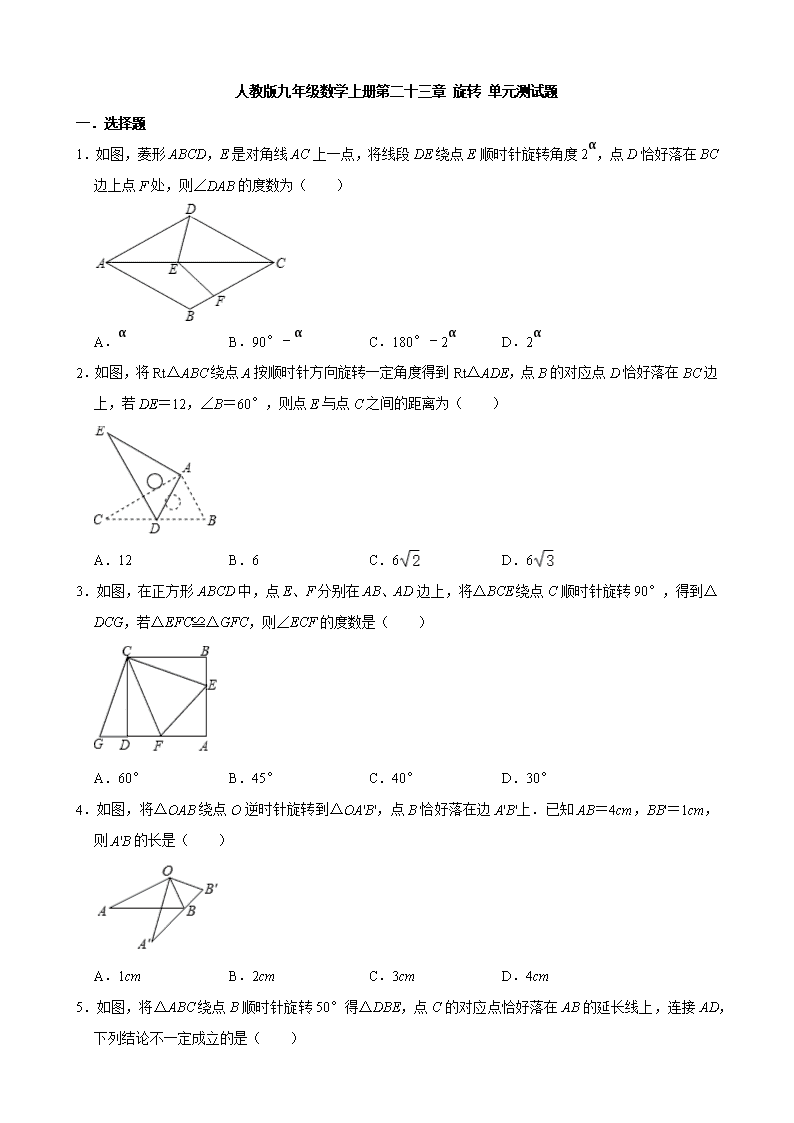
人教版九年级数学上册第二十三章 旋转 单元测试题 一．选择题 1．如图，菱形 ABCD，E 是对角线 AC 上一点，将线段 DE 绕点 E 顺时针旋转角度 2 α ，点 D 恰好落在 BC 边上点 F 处，则∠DAB 的度数为（ ） A． α B．90°﹣ α C．180°﹣2 α D．2 α2．如图，将 Rt△ABC 绕点 A 按顺时针方向旋转一定角度得到 Rt△ADE，点 B 的对应点 D 恰好落在 BC 边 上，若 DE＝12，∠B＝60°，则点 E 与点 C 之间的距离为（ ） A．12 B．6 C．6 D．6 3．如图，在正方形 ABCD 中，点 E、F 分别在 AB、AD 边上，将△BCE 绕点 C 顺时针旋转 90°，得到△ DCG，若△EFC≌△GFC，则∠ECF 的度数是（ ） A．60° B．45° C．40° D．30° 4．如图，将△OAB 绕点 O 逆时针旋转到△OA'B'，点 B 恰好落在边 A'B'上．已知 AB＝4cm，BB'＝1cm，则 A'B 的长是（ ） A．1cm B．2cm C．3cm D．4cm 5．如图，将△ABC 绕点 B 顺时针旋转 50°得△DBE，点 C 的对应点恰好落在 AB 的延长线上，连接 AD， 下列结论不一定成立的是（ ） A．AB＝DB B．∠CBD＝80° C．∠ABD＝∠E D．△ABC≌△DBE 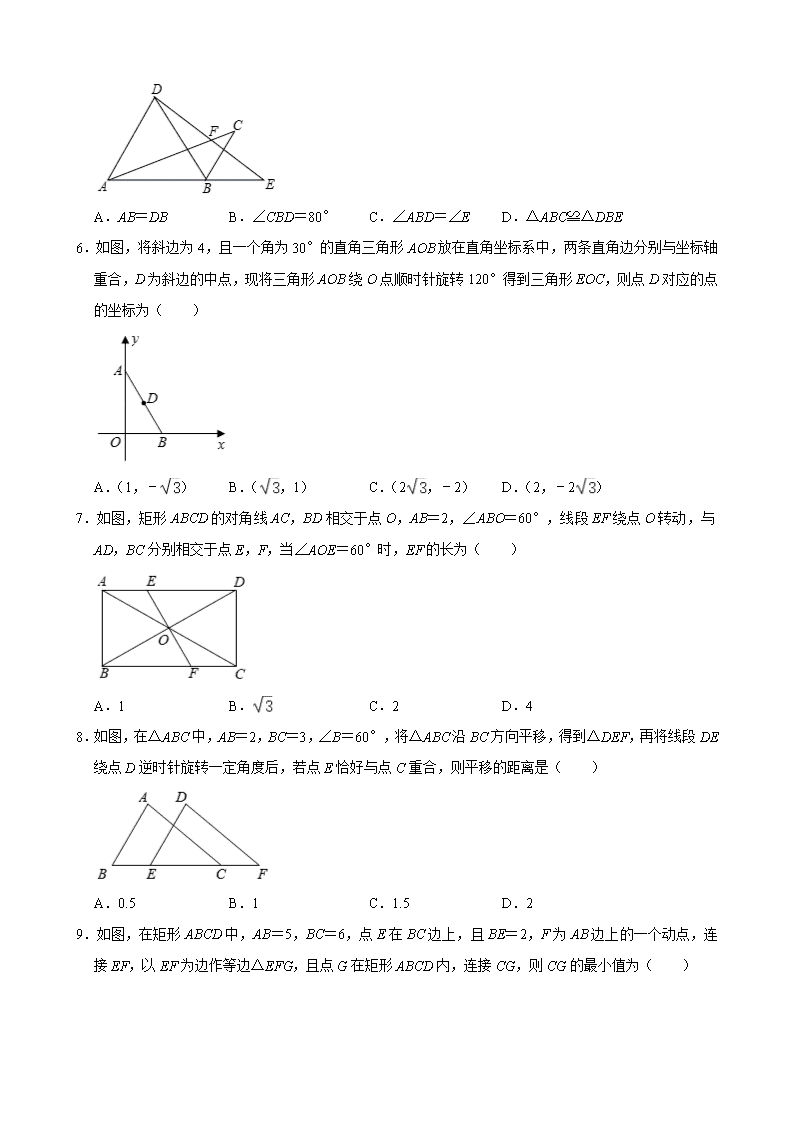6．如图，将斜边为 4，且一个角为 30°的直角三角形 AOB 放在直角坐标系中，两条直角边分别与坐标轴 重合，D 为斜边的中点，现将三角形 AOB 绕 O 点顺时针旋转 120°得到三角形 EOC，则点 D 对应的点 的坐标为（ ） A．（1，﹣ ） B．（ ，1） C．（2 ，﹣2） D．（2，﹣2 ） 7．如图，矩形 ABCD 的对角线 AC，BD 相交于点 O，AB＝2，∠ABO＝60°，线段 EF 绕点 O 转动，与 AD，BC 分别相交于点 E，F，当∠AOE＝60°时，EF 的长为（ ） A．1 B． C．2 D．4 8．如图，在△ABC 中，AB＝2，BC＝3，∠B＝60°，将△ABC 沿 BC 方向平移，得到△DEF，再将线段 DE 绕点 D 逆时针旋转一定角度后，若点 E 恰好与点 C 重合，则平移的距离是（ ） A．0.5 B．1 C．1.5 D．2 9．如图，在矩形 ABCD 中，AB＝5，BC＝6，点 E 在 BC 边上，且 BE＝2，F 为 AB 边上的一个动点，连 接 EF，以 EF 为边作等边△EFG，且点 G 在矩形 ABCD 内，连接 CG，则 CG 的最小值为（ ） A．3 B．2.5 C．4 D．2 10．如图，四边形 ABCD 是正方形，点 E，F 分别在边 CD，BC 上，点 G 在 CB 的延长线上，DE＝CF＝ BG．下列说法： ① 将△DCF 沿某一直线平移可以得到△ABG； ② 将△ABG 沿某一直线对称可以得到 △ADE； ③ 将△ADE 绕某一点旋转可以得到△DCF．其中正确的是（ ） A． ①② B． ②③ C． ①③ D． ①②③二、填空题 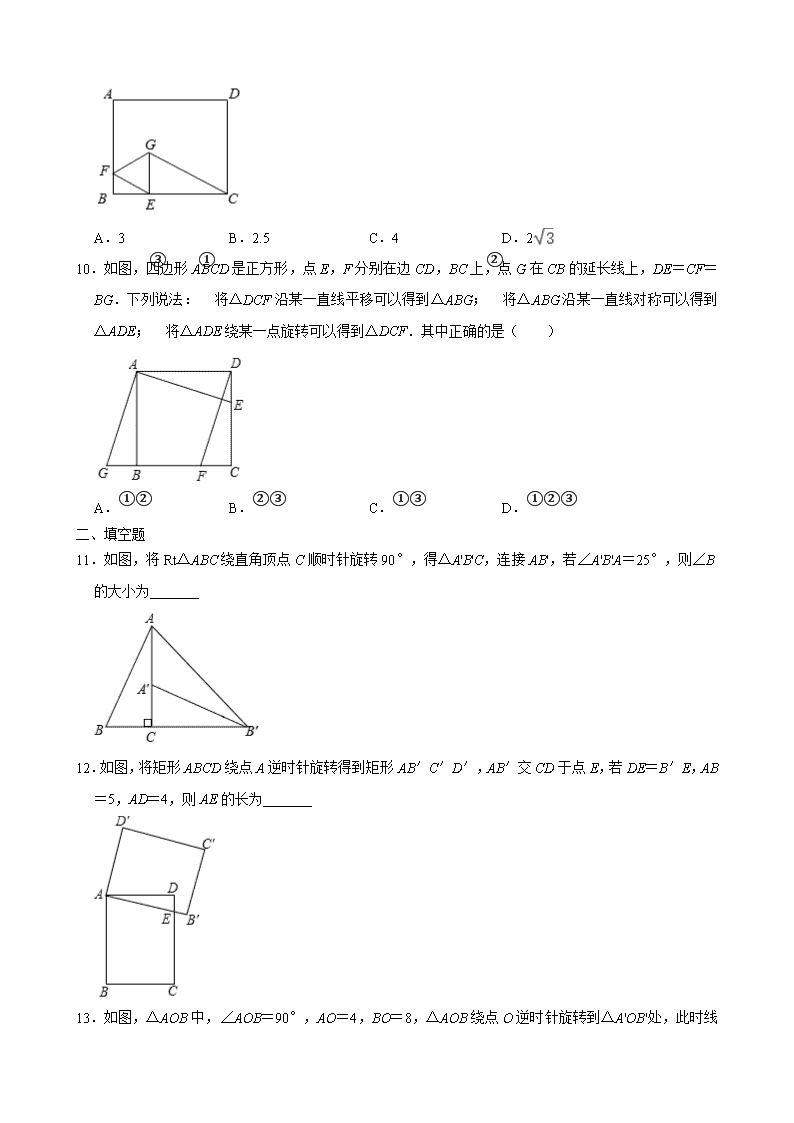11．如图，将 Rt△ABC 绕直角顶点 C 顺时针旋转 90°，得△A'B'C，连接 AB'，若∠A'B'A＝25°，则∠B 的大小为_______ 12．如图，将矩形 ABCD 绕点 A 逆时针旋转得到矩形 AB′C′D′，AB′交 CD 于点 E，若 DE＝B′E， AB＝5，AD＝4，则 AE 的长为_______ 13．如图，△AOB 中，∠AOB＝90°，AO＝4，BO＝8，△AOB 绕点 O 逆时针旋转到△A'OB'处，此时线 段 A'B'与 BO 的交点 E 为 BO 的中点，则线段 B'E 的长度为_______ 14．在平面直角坐标系中，△ABC 三个顶点的坐标分别为 A（2，0）、B（5，0）、C （5，1），将△ABC 绕点 A 逆时针旋转 90°得到△AB'C'，则点 C′的坐标为_______ 15．如图，四边形 ABCD 中，∠DAB＝30°，连接 AC，将△ABC 绕点 B 逆时针旋转 60°，点 C 的对应点 D 重合，得到△EBD，若 AB＝5，AD＝4，则点 AC 的长度为_______ 16．如图，点 E 在正方形 ABCD 的边 CD 上，将△ADE 绕点 A 顺时针旋转 90°到△ABF 的位置，连接 EF， 过点 A 作 EF 的垂线，垂足为点 H，与 BC 交于点 G．若 BG＝3，CG＝2，则 CE 的长为_______ 三、解答题 17．如图，将△ABC 绕点 A 逆时针旋转到△AED，其中点 B 与点 E 是对应点，点 C 与点 D 是对应点，且 DC∥AB，若∠CAB＝65°，求∠CAE 的度数？ 18．如图，在四边形 ABCD 中，∠ABC＝30°，将△DCB 绕点 C 顺时针旋转 60°后，点 D 的对应点恰好 与点 A 重合，得到△ACE，若 AB＝3，BC＝4，求 BD 的长？ 19．如图，在△ABC 中，∠C＝90°，AC＝2，BC＝4，将△ABC 绕点 A 逆时针旋转 90°，使点 C 落在点 E 处，点 B 落在点 D 处，则 B、E 两点间的距离? 20．如图，在正方形 ABCD 中，AB＝4，点 M 在 CD 边上，且 DM＝1，△AEM 与△ADM 关于 AM 所在直 线对称，将△ADM 按顺时针方向绕点 A 旋转 90°得到△ABF，连接 EF，则线段 EF 的长． 21．已知，在等边△ABC 中，点 E 在 BA 的延长线上，点 D 在 BC 上，且 ED＝EC （1）如图 1，求证：AE＝DB； （2）如图 2，将△BCE 绕点 C 顺时针旋转 60°至△ACF（点 B、E 的对应点分别为点 A、F），连接 EF．在 不添加任何辅助线的情况下，请直接写出图中四对线段，使每对线段长度之差等于 AB 的长． 22．已知：如图，在△ABC 中，∠BAC＝120°，以 BC 为边向形外作等边三角形 BCD，把△ABD 绕着点 D 按顺时针方向旋转 60°后得到△ECD，且 A、C、E 三点共线，若 AB＝3，AC＝2，求∠BAD 的度数 与 AD 的长． 23．在△ABC 中，∠ACB＝90°，AC＝BC，直线 MN 经过点 C，且 AD⊥MN 于 D，BE⊥MN 于 E． （1）当直线 MN 绕点 C 旋转到图 1 的位置时，求证：DE＝AD+BE． （2）当直线 MN 绕点 C 旋转到图 2 的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成 立，说明理由． 24．将两块全等的含 30°角的直角三角形按图 1 的方式放置，已知∠BAC＝∠B1A1C1＝30°，则 AB＝2BC． （1）固定三角板 A1B1C，然后将三角板 ABC 绕点 C 顺时针方向旋转至图 2 的位置，AB 与 A1C、A1B1 分别交于点 D、E，AC 与 A1B1 交于点 F． ① 填空：当旋转角等于 20°时，∠BCB1＝ 160 度； ② 当旋转角等于多少度时，AB 与 A1B1 垂直？请说明理由． （2）将图 2 中的三角板 ABC 绕点 C 顺时针方向旋转至图 3 的位置，使 AB∥CB1，AB 与 A1C 交于点 D， 试说明 A1D＝CD． 参考答案 一．选择题 1．如图，菱形 ABCD，E 是对角线 AC 上一点，将线段 DE 绕点 E 顺时针旋转角度 2 α ，点 D 恰好落在 BC 边上点 F 处，则∠DAB 的度数为（ ） A． α B．90°﹣ α C．180°﹣2 α D．2 α【解答】解：如图，连接 BE， ∵四边形 ABCD 是菱形， ∴CD＝BC，∠DAB＝∠DCB，∠ACD＝∠ACB， 在△DCE 和△BCE 中， ， ∴△DCE≌△BCE（SAS）， ∴DE＝BE，∠EDC＝∠EBC， ∵将线段 DE 绕点 E 顺时针旋转角度 2 α ， ∴DE＝EF，∠DEF＝2 α ， ∴BE＝DE＝EF， ∴∠EBF＝∠EFB， ∴∠EDC＝∠EBC＝∠EFB， ∵∠EFB+∠EFC＝180°， ∴∠EDC+∠EFC＝180°， ∵∠EDC+∠EFC+∠DEF+∠DCF＝360°， ∴∠DCF＝180°﹣2 α ＝∠DAB， 故选：C． 2．如图，将 Rt△ABC 绕点 A 按顺时针方向旋转一定角度得到 Rt△ADE，点 B 的对应点 D 恰好落在 BC 边 上，若 DE＝12，∠B＝60°，则点 E 与点 C 之间的距离为（ ） A．12 B．6 C．6 D．6 【解答】解：如图，连接 EC， ∵将 Rt△ABC 绕点 A 按顺时针方向旋转一定角度得到 Rt△ADE， ∴DE＝BC＝12，AD＝AB，AC＝AE，∠DAB＝∠EAC， ∵∠B＝60°， ∴∠ACB＝30°， ∴AB＝ BC＝6，AC＝ AB＝6 ， ∵AD＝AB，∠B＝60°， ∴△ABD 是等边三角形， ∴∠DAB＝60°＝∠EAC， ∴△ACE 是等边三角形， ∴AC＝AE＝EC＝6 ， 故选：D． 3．如图，在正方形 ABCD 中，点 E、F 分别在 AB、AD 边上，将△BCE 绕点 C 顺时针旋转 90°，得到△ DCG，若△EFC≌△GFC，则∠ECF 的度数是（ ） A．60° B．45° C．40° D．30° 【解答】解：∵将△BCE 绕点 C 顺时针旋转 90°， ∴∠BCE＝∠GCD， ∵△EFC≌△GFC， ∴∠ECF＝∠GCF， ∴∠ECF＝∠GCD+∠DCF＝∠BCE+∠DCF， ∴∠ECF＝ ∠BCD＝45°， 故选：B． 4．如图，将△OAB 绕点 O 逆时针旋转到△OA'B'，点 B 恰好落在边 A'B'上．已知 AB＝4cm，BB'＝1cm，则 A'B 的长是（ ） A．1cm B．2cm C．3cm D．4cm 【解答】解：∵将△OAB 绕点 O 按逆时针方向旋转至△OA′B′， ∴△OAB≌△OA′B′， ∴AB＝A′B′＝4， ∴A′B＝A′B′﹣BB′＝4﹣1＝3（cm）， 故选：C． 5．如图，将△ABC 绕点 B 顺时针旋转 50°得△DBE，点 C 的对应点恰好落在 AB 的延长线上，连接 AD， 下列结论不一定成立的是（ ） A．AB＝DB B．∠CBD＝80° C．∠ABD＝∠E D．△ABC≌△DBE 【解答】解：∵将△ABC 绕点 B 顺时针旋转 50°得△DBE， ∴△ABC≌△DBE，∠ABD＝∠CBE＝50°， ∴AB＝DB，∠CBD＝80°， ∵∠ABD＝∠E+∠BDE， ∴∠ABD≠∠E， 故选：C． 6．如图，将斜边为 4，且一个角为 30°的直角三角形 AOB 放在直角坐标系中，两条直角边分别与坐标轴 重合，D 为斜边的中点，现将三角形 AOB 绕 O 点顺时针旋转 120°得到三角形 EOC，则点 D 对应的点 的坐标为（ ） A．（1，﹣ ） B．（ ，1） C．（2 ，﹣2） D．（2，﹣2 ） 【解答】解：根据题意画出△AOB 绕着 O 点顺时针旋转 120°得到的△A′OB′，连接 OD，OD′， 过 D′作 DM⊥y 轴， ∴∠DOD′＝120°， ∵D 为斜边 AB 的中点， ∵AD＝OD＝ AB＝2， ∴∠BAO＝∠DOA＝30°， ∴∠MOD′＝30°， 在 Rt△OMD′中，OD′＝OD＝2， ∴MD′＝1，OM＝ ， 则 D 的对应点 D′的坐标为（1，﹣ ）， 故选：A． 7．如图，矩形 ABCD 的对角线 AC，BD 相交于点 O，AB＝2，∠ABO＝60°，线段 EF 绕点 O 转动，与 AD，BC 分别相交于点 E，F，当∠AOE＝60°时，EF 的长为（ ） A．1 B． C．2 D．4 【解答】解：∵四边形 ABCD 是矩形， ∴OA＝OB，∠ABC＝∠BAD＝90°， 又∵∠ABO＝60°， ∴△ABO 为等边三角形， ∴∠BAO＝60°， ∴∠OAE＝30°， ∵线段 EF 绕点 O 转动，∠AOE＝60°， ∴∠AEO＝180°﹣60°﹣30°＝90°， ∴四边形 ABFE 为矩形， ∴AB＝EF＝2． 故选：C． 8．如图，在△ABC 中，AB＝2，BC＝3，∠B＝60°，将△ABC 沿 BC 方向平移，得到△DEF，再将线段 DE 绕点 D 逆时针旋转一定角度后，若点 E 恰好与点 C 重合，则平移的距离是（ ） A．0.5 B．1 C．1.5 D．2 【解答】解：连接 DC， ∵∠B＝60°，将△ABC 沿射线 BC 的方向平移，得到△DEF，再将线段 DE 绕点 D 逆时针旋转一定角 度后，若点 E 恰好与点 C 重合， ∴∠DEF＝60°，AB＝DE＝DC＝2， ∴△DEC 是等边三角形， ∴EC＝DE＝2， ∴BE＝BC﹣EC＝3﹣2＝1． 故选：B． 9．如图，在矩形 ABCD 中，AB＝5，BC＝6，点 E 在 BC 边上，且 BE＝2，F 为 AB 边上的一个动点，连 接 EF，以 EF 为边作等边△EFG，且点 G 在矩形 ABCD 内，连接 CG，则 CG 的最小值为（ ） A．3 B．2.5 C．4 D．2 【解答】解：由题意可知，点 F 是主动点，点 G 是从动点，点 F 在线段上运动，点 G 也一定在直线轨 迹上运动， 将△EFB 绕点 E 旋转 60°，使 EF 与 EG 重合，得到△EFB≌△EHG， 从而可知△EBH 为等边三角形，点 G 在垂直于 HE 的直线 HN 上， 作 CM⊥HN，则 CM 即为 CG 的最小值， 作 EP⊥CM，可知四边形 HEPM 为矩形， 则 CM＝MP+CP＝HE+ EC＝2+2＝4， 故选：C． 10．如图，四边形 ABCD 是正方形，点 E，F 分别在边 CD，BC 上，点 G 在 CB 的延长线上，DE＝CF＝ BG．下列说法： ① 将△DCF 沿某一直线平移可以得到△ABG； ② 将△ABG 沿某一直线对称可以得到 △ADE； ③ 将△ADE 绕某一点旋转可以得到△DCF．其中正确的是（ ） A． ①② B． ②③ C． ①③ D． ①②③【解答】解：∵四边形 ABCD 是正方形， ∴AB＝AD＝CD，∠ABC＝∠ADE＝∠DCB＝90°， 又∵DE＝CF， ∴△ADE≌△DCF（SAS）， 同理可得：△ADE≌△ABG，△ABG≌△DCF， ∴将△DCF 沿某一直线平移可以得到△ABG，故 ① 正确； 将△ABG 绕点 A 旋转可以得到△ADE，故 ② 错误； 将△ADE 绕线段 AD，CD 的垂直平分线的交点旋转可以得到△DCF，故 ③ 正确； 故选：C． 四、填空题 11．如图，将 Rt△ABC 绕直角顶点 C 顺时针旋转 90°，得△A'B'C，连接 AB'，若∠A'B'A＝25°，则∠B 的大小为（ ） 【解答】解：∵将 Rt△ABC 绕直角顶点 C 顺时针旋转 90°，得△A'B'C， ∴∠B＝∠CA'B'，AC＝B'C，∠ACB'＝90°， ∴∠CAB'＝45°， ∴∠CA'B'＝∠CAB'+∠A'B'A＝45°+25°＝70°， 12．如图，将矩形 ABCD 绕点 A 逆时针旋转得到矩形 AB′C′D′，AB′交 CD 于点 E，若 DE＝B′E， AB＝5，AD＝4，则 AE 的长为（ ） 【解答】解：∵将矩形 ABCD 绕点 A 逆时针旋转得到矩形 AB′C′D′， ∴AB′＝AB＝5， ∵DE＝B′E， ∴AE＝CE， 设 AE＝CE＝x， ∴DE＝5﹣x， ∵∠D＝90°， ∴AD2 +DE2＝AE2， 即 42+（5﹣x）2＝x2， 解得：x＝ ， ∴AE＝ ， 13．如图，△AOB 中，∠AOB＝90°，AO＝4，BO＝8，△AOB 绕点 O 逆时针旋转到△A'OB'处，此时线 段 A'B'与 BO 的交点 E 为 BO 的中点，则线段 B'E 的长度为（ ） 【解答】解：∵∠AOB＝90°，AO＝4，BO＝8， ∴AB＝ ＝ ＝4 ， ∵△AOB 绕顶点 O 逆时针旋转到△A′OB′处， ∴AO＝A′O＝4，A′B′＝AB＝4 ， ∵点 E 为 BO 的中点， ∴OE＝ BO＝ ×8＝4， ∴OE＝A′O＝4， 过点 O 作 OF⊥A′B′于 F， S△A′OB′＝ ×4 •OF＝ ×4×8， 解得 OF＝ ， 在 Rt△EOF 中，EF＝ ＝ ＝ ， ∵OE＝A′O，OF⊥A′B′， ∴A′E＝2EF＝2× ＝ ， ∴B′E＝A′B′﹣A′E＝4 ﹣ ＝ ； 14．在平面直角坐标系中，△ABC 三个顶点的坐标分别为 A（2，0）、B（5，0）、C （5，1），将△ABC 绕点 A 逆时针旋转 90°得到△AB'C'，则点 C′的坐标为（ ） 【解答】解：∵△ABC 三个顶点的坐标分别为 A（2，0）、B（5，0）、C （5，1）， 将△ABC 绕点 A 逆时针旋转 90°得到△AB'C'，如图所示： 则点 C′的坐标为（1，3）． 15．如图，四边形 ABCD 中，∠DAB＝30°，连接 AC，将△ABC 绕点 B 逆时针旋转 60°，点 C 的对应点 D 重合，得到△EBD，若 AB＝5，AD＝4，则点 AC 的长度为（ ） 【解答】解：∵△EBD 是由△ABC 旋转得到， ∴BA＝BE，∠ABE＝60°，AC＝DE， ∴△ABE 是等边三角形， ∴∠EAB＝60°， ∵∠BAD＝30°， ∴∠EAD＝90°， ∵AE＝AB＝5，AD＝4， ∴DE＝ ＝ ＝ ， 16．如图，点 E 在正方形 ABCD 的边 CD 上，将△ADE 绕点 A 顺时针旋转 90°到△ABF 的位置，连接 EF， 过点 A 作 EF 的垂线，垂足为点 H，与 BC 交于点 G．若 BG＝3，CG＝2，则 CE 的长为（ ） 【解答】解：如图所示，连接 EG， 由旋转可得，△ADE≌△ABF， ∴AE＝AF，DE＝BF， 又∵AG⊥EF， ∴H 为 EF 的中点， ∴AG 垂直平分 EF， ∴EG＝FG， 设 CE＝x，则 DE＝5﹣x＝BF，FG＝8﹣x， ∴EG＝8﹣x， ∵∠C＝90°， ∴Rt△CEG 中，CE2+CG2＝EG2，即 x2+22＝（8﹣x）2， 解得 x＝ ， ∴CE 的长为 ， 五、解答题 17．如图，将△ABC 绕点 A 逆时针旋转到△AED，其中点 B 与点 E 是对应点，点 C 与点 D 是对应点，且 DC∥AB，若∠CAB＝65°，求∠CAE 的度数？ 【解答】解：∵DC∥AB， ∴∠CAB＝∠DCA＝65°， ∵将△ABC 绕点 A 逆时针旋转到△AED， ∴AC＝AD，∠DAE＝∠CAB＝65°， ∵∠ADC＝∠ACD＝65°， ∴∠DAC＝50°， ∴∠CAE＝∠DAE﹣∠DAC＝15°， 18．如图，在四边形 ABCD 中，∠ABC＝30°，将△DCB 绕点 C 顺时针旋转 60°后，点 D 的对应点恰好 与点 A 重合，得到△ACE，若 AB＝3，BC＝4，求 BD 的长？ 【解答】解：连接 BE，如图， ∵△DCB 绕点 C 顺时针旋转 60°后，点 D 的对应点恰好与点 A 重合，得到△ACE， ∴∠BCE＝60°，CB＝CE，BD＝AE， ∴△BCE 为等边三角形， ∴BE＝BC＝4，∠CBE＝60°， ∵∠ABC＝30°， ∴∠ABE＝90°， 在 Rt△ABE 中，AE＝ ＝5， ∴BD＝5． 19．如图，在△ABC 中，∠C＝90°，AC＝2，BC＝4，将△ABC 绕点 A 逆时针旋转 90°，使点 C 落在点 E 处，点 B 落在点 D 处，则 B、E 两点间的距离为（ ） 【解答】解：如图，延长 DE 交 BC 于 F， ∵将△ABC 绕点 A 逆时针旋转 90°， ∴AE＝AC＝2，∠EAC＝90°＝∠DEA＝∠ACB， ∴AE∥CB，AC∥EF， ∴CF＝EF＝2＝AC，∠EFC＝90°， ∴BF＝2， ∴BE＝ ＝ ＝2 ， 20．如图，在正方形 ABCD 中，AB＝4，点 M 在 CD 边上，且 DM＝1，△AEM 与△ADM 关于 AM 所在直 线对称，将△ADM 按顺时针方向绕点 A 旋转 90°得到△ABF，连接 EF，则线段 EF 的长． 【解答】解：如图，连接 BM． ∵△AEM 与△ADM 关于 AM 所在的直线对称， ∴AE＝AD，∠MAD＝∠MAE． ∵△ADM 按照顺时针方向绕点 A 旋转 90°得到△ABF， ∴AF＝AM，∠FAB＝∠MAD． ∴∠FAB＝∠MAE ∴∠FAB+∠BAE＝∠BAE+∠MAE． ∴∠FAE＝∠MAB． ∴△FAE≌△MAB（SAS）． ∴EF＝BM． ∵四边形 ABCD 是正方形， ∴BC＝CD＝AB＝4． ∵DM＝1， ∴CM＝3． ∴在 Rt△BCM 中，BM＝ ＝5， ∴EF＝5， 21．已知，在等边△ABC 中，点 E 在 BA 的延长线上，点 D 在 BC 上，且 ED＝EC （1）如图 1，求证：AE＝DB； （2）如图 2，将△BCE 绕点 C 顺时针旋转 60°至△ACF（点 B、E 的对应点分别为点 A、F），连接 EF．在 不添加任何辅助线的情况下，请直接写出图中四对线段，使每对线段长度之差等于 AB 的长． 【解答】解：（1）如图，作 DK∥AC 交 AB 于 K，则△BDK 是等边三角形， ∵△ABC 是等边三角形， ∴∠EKD＝∠EAC＝120°，∠B＝∠BKD＝60°， ∴DK＝BD， ∵ED＝EC， ∴∠EDC＝∠ECD， ∴∠B+∠KED＝∠EDC， ∵∠ECA+∠ACB＝∠ECD， ∴∠B+∠KED＝∠ECA+∠ACB， ∵∠B＝∠ACB＝60°， ∴∠KED＝∠ECA， 在△DKE 与△EAC 中， ， ∴△DKE≌△EAC（AAS）， ∴AE＝DK， ∴BD＝AE． （2）BE﹣AE＝AB；BE﹣BD＝AB；AF﹣AE＝AB；AF﹣BD＝AB． 理由：由旋转可得，△BCE≌△ACF， ∴BE＝AF， 又∵BD＝AE，AB＝BE﹣AE， ∴BE﹣AE＝AB；BE﹣BD＝AB；AF﹣AE＝AB；AF﹣BD＝AB． 22．已知：如图，在△ABC 中，∠BAC＝120°，以 BC 为边向形外作等边三角形 BCD，把△ABD 绕着点 D 按顺时针方向旋转 60°后得到△ECD，且 A、C、E 三点共线，若 AB＝3，AC＝2，求∠BAD 的度数 与 AD 的长． 【解答】解：∵△ABD 绕着点 D 按顺时针方向旋转 60°后得到△ECD， ∴∠ADE＝60°，DA＝DE， ∴△ADE 为等边三角形， ∴∠DAE＝60°． ∵点 A、C、E 在一条直线上， ∴∠BAD＝∠BAC﹣∠DAE＝120°﹣60°＝60°． ∵点 A、C、E 在一条直线上， ∴AE＝AC+CE． ∵△ABD 绕着点 D 按顺时针方向旋转 60°后得到△ECD， ∴CE＝AB， ∴AE＝AC+AB＝2+3＝5． ∵△ADE 为等边三角形， ∴AD＝AE＝5． 23．在△ABC 中，∠ACB＝90°，AC＝BC，直线 MN 经过点 C，且 AD⊥MN 于 D，BE⊥MN 于 E． （1）当直线 MN 绕点 C 旋转到图 1 的位置时，求证：DE＝AD+BE． （2）当直线 MN 绕点 C 旋转到图 2 的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成 立，说明理由． 【解答】证明：（1）∵AD⊥DE，BE⊥DE， ∴∠ADC＝∠BEC＝90°， ∵∠ACB＝90°， ∴∠ACD+∠BCE＝90°，∠DAC+∠ACD＝90°， ∴∠DAC＝∠BCE， 在△ADC 和△CEB 中 ∴△ADC≌△CEB（AAS）， ∴AD＝CE，CD＝BE， ∵DC+CE＝DE， ∴AD+BE＝DE． （2）DE＝AD﹣BE， 理由：∵BE⊥EC，AD⊥CE， ∴∠ADC＝∠BEC＝90°， ∴∠EBC+∠ECB＝90°， ∵∠ACB＝90°， ∴∠ECB+∠ACE＝90°， ∴∠ACD＝∠EBC， 在△ADC 和△CEB 中， ， ∴△ADC≌△CEB（AAS）， ∴AD＝CE，CD＝BE， ∴DE＝EC﹣CD＝AD﹣BE． 24．将两块全等的含 30°角的直角三角形按图 1 的方式放置，已知∠BAC＝∠B1A1C1＝30°，则 AB＝2BC． （1）固定三角板 A1B1C，然后将三角板 ABC 绕点 C 顺时针方向旋转至图 2 的位置，AB 与 A1C、A1B1 分别交于点 D、E，AC 与 A1B1 交于点 F． ① 填空：当旋转角等于 20°时，∠BCB1＝ 160 度； ② 当旋转角等于多少度时，AB 与 A1B1 垂直？请说明理由． （2）将图 2 中的三角板 ABC 绕点 C 顺时针方向旋转至图 3 的位置，使 AB∥CB1，AB 与 A1C 交于点 D， 试说明 A1D＝CD． 【解答】解：（1） ① 由旋转的性质得，∠ACA1＝20°， ∴∠BCD＝∠ACB﹣∠ACA1＝90°﹣20°＝70°， ∴∠BCB1＝∠BCD+∠A1CB1， ＝70°+90°， ＝160°； ② 当 AB 与 A1B1 垂直时，∠AED＝90°， ∴∠A1DE＝90°﹣∠A1＝90°﹣30°＝60°， ∴∠BDC＝∠A1DE＝60°，由已知易得∠B＝60°， ∴∠DCB＝180°﹣∠BDC﹣∠B＝60°， ∴∠ACA1＝30°， 即当旋转角等于 30°时，AB 与 A1B1 垂直． （2）∵AB∥CB1， ∴∠ADC＝180°﹣∠A1CB1＝180°﹣90°＝90°， ∵∠BAC＝30°， ∴CD＝ AC， 又∵由旋转的性质得，A1C＝AC， ∴A1D＝CD．