北师大版九年级数学《圆》复习导学案+数学教学计划 18页

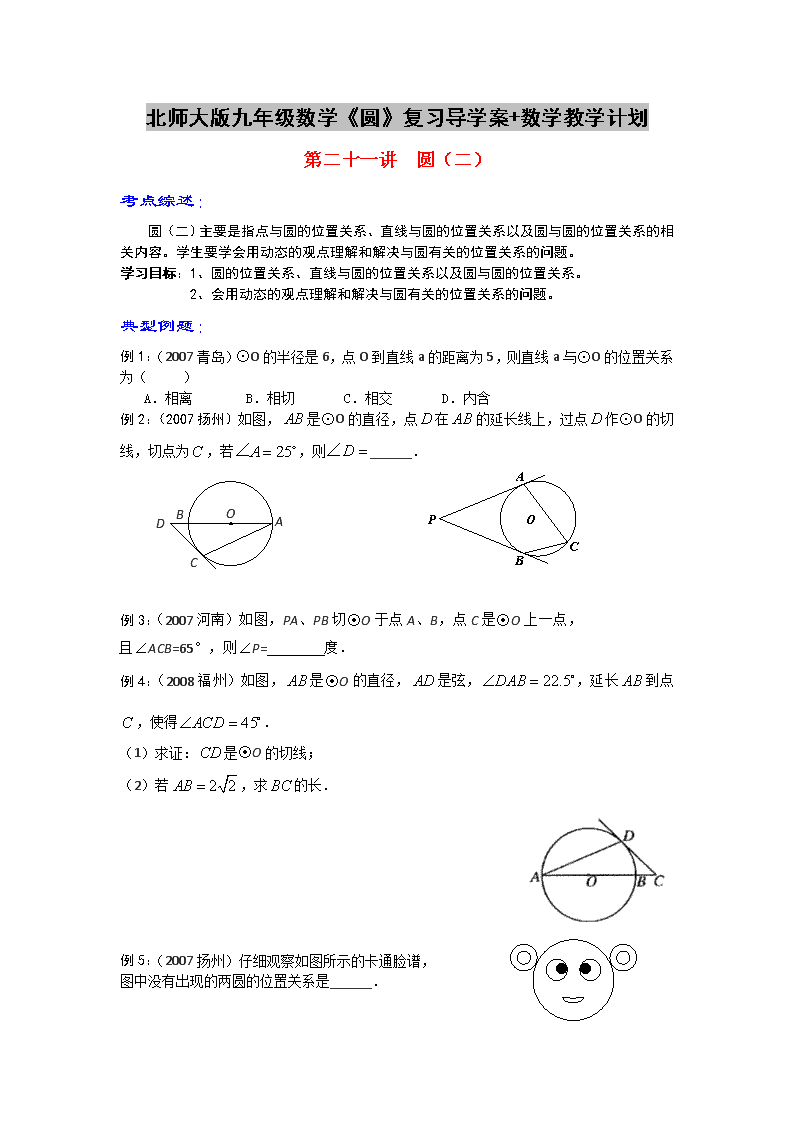
北师大版九年级数学《圆》复习导学案+数学教学计划 第二十一讲 圆（二） 考点综述： 圆（二）主要是指点与圆的位置关系、直线与圆的位置关系以及圆与圆的位置关系的相 关内容。学生要学会用动态的观点理解和解决与圆有关的位置关系的问题。 学习目标：1、圆的位置关系、直线与圆的位置关系以及圆与圆的位置关系。 2、会用动态的观点理解和解决与圆有关的位置关系的问题。 典型例题： 例 1：（2007 青岛）⊙O 的半径是 6，点 O 到直线 a 的距离为 5，则直线 a 与⊙O 的位置关系 为（ ） A．相离 B．相切 C．相交 D．内含 例 2：（2007 扬州）如图， AB 是⊙O 的直径，点 D 在 AB 的延长线上，过点 D 作⊙O 的切 线，切点为C ，若 25A  ∠ ，则 D ∠ ______． 例 3：（2007 河南）如图，PA、PB 切⊙O 于点 A、B，点 C 是⊙O 上一点， 且∠ACB=65°，则∠P= 度． 例 4：（2008 福州）如图，AB 是⊙O 的直径，AD 是弦， 22.5DAB   ，延长 AB 到点C ， 使得 45ACD   ． （1）求证：CD 是⊙O 的切线； （2）若 2 2AB  ，求 BC 的长． 例 5：（2007 扬州）仔细观察如图所示的卡通脸谱， 图中没有出现的两圆的位置关系是______． OB AD C O C B A P 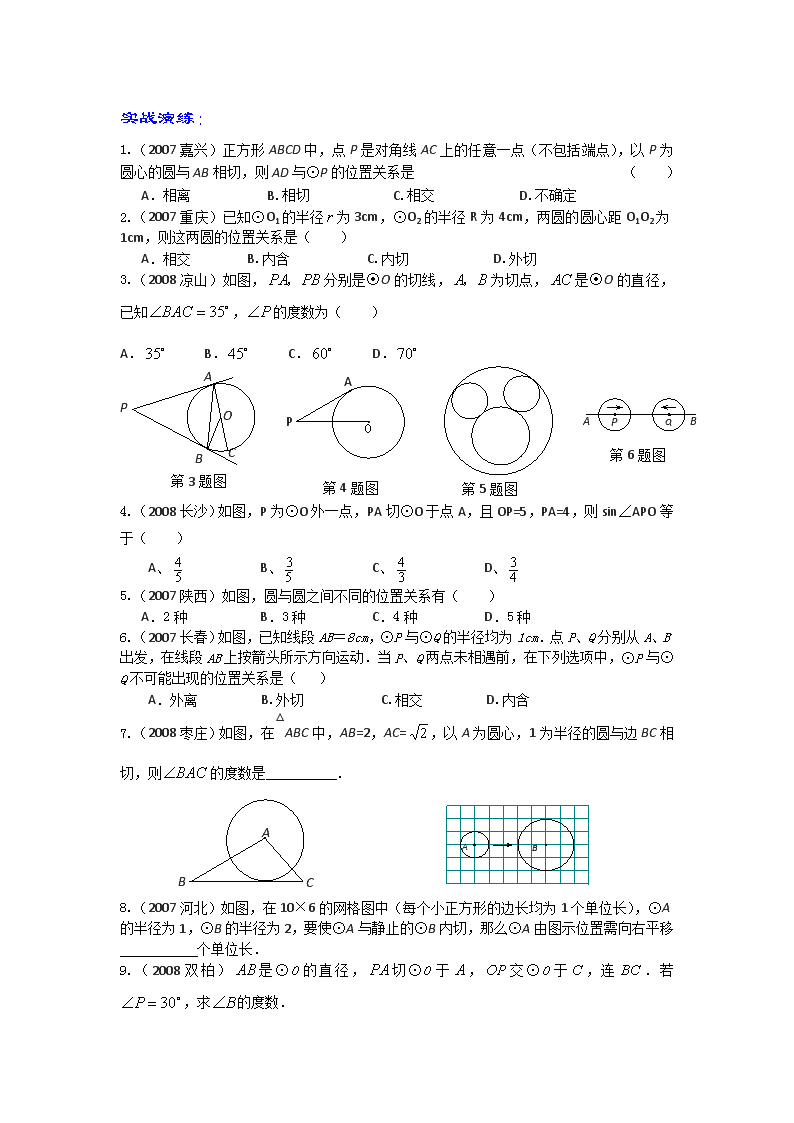实战演练： 1.（2007 嘉兴）正方形 ABCD 中，点 P 是对角线 AC 上的任意一点（不包括端点），以 P 为 圆心的圆与 AB 相切，则 AD 与⊙P 的位置关系是 （ ） A．相离 B.相切 C.相交 D.不确定 2.（2007 重庆）已知⊙O1 的半径 r 为 3cm，⊙O2 的半径 R 为 4cm，两圆的圆心距 O1O2 为 1cm，则这两圆的位置关系是（ ） A．相交 B.内含 C.内切 D.外切 3.（2008 凉山）如图， PA PB， 分别是⊙O 的切线， A B， 为切点， AC 是⊙O 的直径， 已知 35BAC   ， P 的度数为（ ） A．35 B． 45 C． 60 D． 70 第 4 题图 4.（2008 长沙）如图，P 为⊙O 外一点，PA 切⊙O 于点 A，且 OP=5，PA=4，则 sin∠APO 等 于（ ） A、 5 4 B、 5 3 C、 3 4 D、 4 3 5.（2007 陕西）如图，圆与圆之间不同的位置关系有（ ） A．2 种 B．3 种 C．4 种 D．5 种 6.（2007 长春）如图，已知线段 AB＝8cm，⊙P 与⊙Q 的半径均为 1cm．点 P、Q 分别从 A、B 出发，在线段 AB 上按箭头所示方向运动．当 P、Q 两点未相遇前，在下列选项中，⊙P 与⊙ Q 不可能出现的位置关系是（ ） A．外离 B.外切 C.相交 D.内含 7.（2008 枣庄）如图，在△ABC 中，AB=2，AC= 2 ，以 A 为圆心，1 为半径的圆与边 BC 相切，则 BAC 的度数是 ． 8.（2007 河北）如图，在 10×6 的网格图中（每个小正方形的边长均为 1 个单位长），⊙A 的半径为 1，⊙B 的半径为 2，要使⊙A 与静止的⊙B 内切，那么⊙A 由图示位置需向右平移 ___________个单位长． 9.（2008 双柏）AB 是⊙O 的直径，PA 切⊙O 于 A ，OP 交⊙O 于C ，连 BC ．若 30P   ， 求 B 的度数． 第 3 题图 A B C OP P O A · 第 5 题图 P 第 6 题图 QA B A B C BA 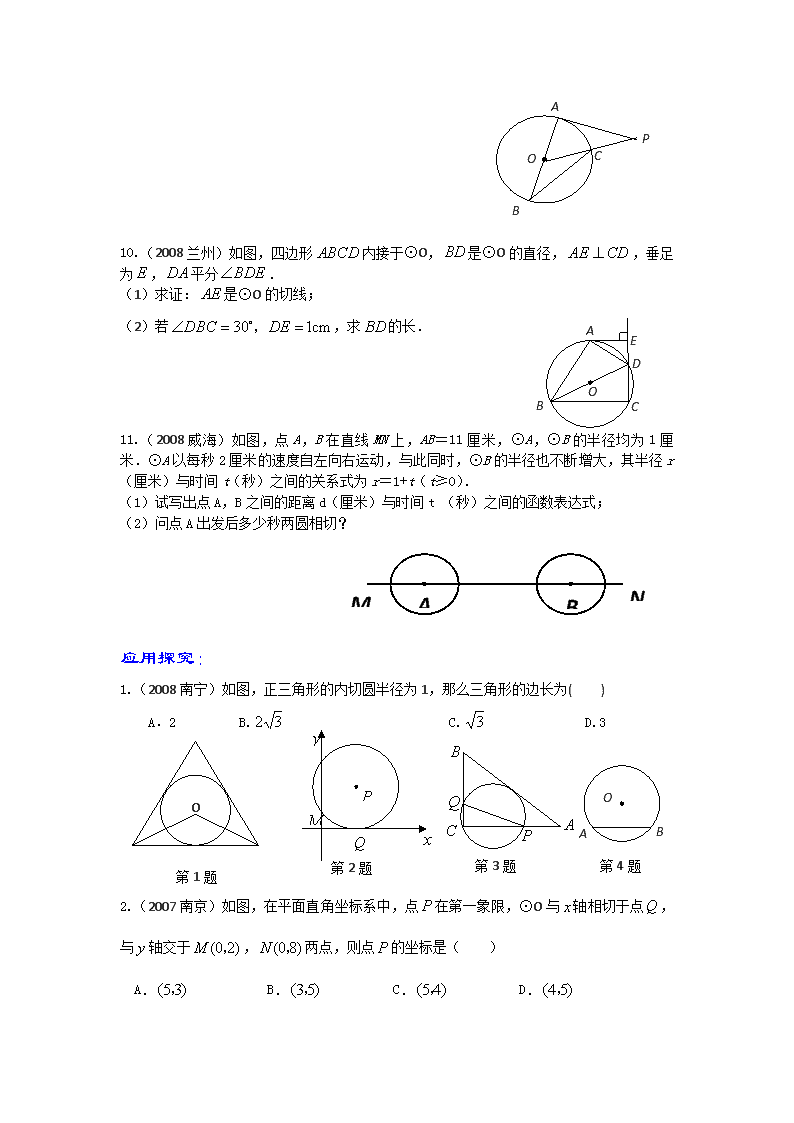10.（2008 兰州）如图，四边形 ABCD 内接于⊙O， BD 是⊙O 的直径， AE CD ，垂足 为 E ， DA 平分 BDE ． （1）求证： AE 是⊙O 的切线； （2）若 30 1cmDBC DE  ， ，求 BD 的长． 11.（2008 威海）如图，点 A，B 在直线 MN 上，AB＝11 厘米，⊙A，⊙B 的半径均为 1 厘米．⊙ A 以每秒 2 厘米的速度自左向右运动，与此同时，⊙B 的半径也不断增大，其半径 r（厘米） 与时间 t（秒）之间的关系式为 r＝1+t（t≥0）． （1）试写出点 A，B 之间的距离 d（厘米）与时间 t （秒）之间的函数表达式； （2）问点 A 出发后多少秒两圆相切？ 应用探究： 1.（2008 南宁）如图，正三角形的内切圆半径为 1，那么三角形的边长为( ) A．2 B. 32 C. 3 D.3 第 1 题 2.（2007 南京）如图，在平面直角坐标系中，点 P 在第一象限，⊙O 与 x 轴相切于点 Q ， 与 y 轴交于 (0 2)M ， ， (0 8)N ， 两点，则点 P 的坐标是（ ） A． (5 3)， B． (3 5)， C． (5 4)， D． (4 5)， A B NM A B C P O D E CB O A O Q P O N x y M 第 2 题 第 3 题 A B C Q P O BA 第 4 题 3.（2007 常州）如图，在 ABC△ 中， 10AB  ， 8AC  ， 6BC  ，经过点C 且与边 AB 相切的动圆与CA CB， 分别相交于点 P Q， ，则线段 PQ 长度的最小值是（ ） A． 4.75 B． 4.8 C．5 D． 4 2 4.（2008 河北）如图 3，已知⊙O 的半径为 5，点O 到弦 AB 的距离为 3，则⊙O 上 到弦 AB 所在直线的距离为 2 的点有（ ） A．1 个 B．2 个 C．3 个 D．4 个 5.（2008 南京）如图，已知⊙O 的半径为 6cm，射线 PM 经过点 O ， 10cmOP  ，射线 PN 与⊙O 相切于点Q ． A B， 两点同时从点 P 出发，点 A 以 5cm/s 的速度沿射线 PM 方向运 动，点 B 以 4cm/s 的速度沿射线 PN 方向运动．设运动时间为t s． （1）求 PQ 的长； （2）当t 为何值时，直线 AB 与⊙O 相切？ 1.4 解直角三角形 执笔： 审核：九年级备课组 课型：新授 授课时间： 【学习目标】1、了解仰角、俯角的概念，使学生根据直角三角形的知识解决实 际问题． 2、理解直角三角形中五个元素的关系，会运用勾股定理，直角三 角形的两个锐角互余及锐角三角函数解直角三角形 【学习重点】1、直角三角形的解法． 2、将某些实际问题中的数量关系，归结为直角三角形元素之间的 关系，从而利用所学知识把实际问题解决 【学习难点】三角函数在解直角三角形中的灵活运用实际问题转化成数学模型 【学习过程】 一、预习导学 （第 5 题） A B Q OP N M 直角三角形 ABC 中，∠C=90°，a、b、c、∠A、∠B 这五个元素间有哪些等量关 系呢？ (1)勾股定理： (2)锐角之间的关系： (3) 边 角 之 间 关 系 ： 二、合作交流 1、在△ABC 中，∠C 为直角，∠A、∠B、∠C 所对的边分别为 a、b、c，且 b= 2 ， a= 6 ，解这个三角形． 2、在 Rt△ABC 中，∠C 为直角， ∠B =30o，b=20，解这个三角形． 三、教师点拔 当我们进行测量时，在视线与水平线所成的角中， 视线在水平线上方的角叫做仰角，在水平线下方的角叫做俯角． 四、学生展示 1、根据直角三角形的__________元素（至少有一个边），求出其它所有元素的过 程，即解直角三角形． 2、Rt△ABC 中，若 sinA= 4 5 ，AB=10，那么 BC=_____，tanB=______． 3、在△ABC 中，∠C=90°，AC=6，BC=8，那么 sinA=________． 4、在△ABC 中，∠C=90°，sinA= 3 5 ，则 cosA 的值是（ ） A． 3 5 B． 4 5 C． 9 16.25 25D 5、在 Rt△ABC 中，∠C=90°，a=5，b=12，解这个直角三角形． 6、 在△ABC 中，∠C 为直角，AC=6， BAC 的平分线 AD=4 3 ，解此直角三角 形。 五、课堂小结 六、课后作业 1、如图,由 D 点测塔顶 A 点和塔基 B 点仰角分别为 60°和 30°.已知塔基高出地 平面 20 米(即 BC 为 20 米)塔身 AB 的高为_____________米； 2、如图敌机从一高炮正上方 2000 米经过,沿水平方向飞行,稍后到达 B 点, 这时仰角为 45°,1 分钟后,飞机到达 A 点,仰角 30°,则飞机从 B 到 A 的 速度是____________米/秒； 3、如图所示,河对岸有水塔 CD.今在 A 处测得塔顶 C 的仰角为 30°, 前进 20 米到达 B 处,又测得 C 的仰角为 45°,则塔高 CD 是____________米； 4、如图：在 200米高的峭壁上,测得一塔的塔顶与塔基的俯角分别为30°和 60°, 那么塔高是_________米 5、如图：从 B 处测得建筑物上旗杆 EC 顶点 C 的仰角是 60°,再从 B 的正上方 40 米高层上 A 处,测得 C 的仰角是 45°,那么旗杆顶点 C 离地 CD 的高度是 ___________米. 6、如图：已知在一峭壁顶点 B 测得地面上一点 A 俯角 60°,竖直下降 10 米至 D, 测得 A 点俯角 45°,那么峭壁的高是_____________米. （4 题图） （5 题图） （6 题图） 7、从山顶 D 测得同一方向的 A、B 两点，俯角分别为 30°,60°,已知 AB=140 米, 求山高(A、B 与山底在同一水平面上).(答案可带根号) 8、从与塔底在同一水平线的测量仪上,测得塔顶的仰角为 45°,向塔前进 10 米,(两次测量在塔的同侧)又测得塔顶的仰角为 60°,测量仪高是 1.5 米,求 塔高(精确到 0.1 米). 9、两山脚 B、C 相距 1500 米,在距山脚 B 500 米处 A 点,测得山 BD、CE 的山顶 D、E 仰角分别为 45°,30°.求两山的高(精确到 1 米). 10、如图：山顶上有高为 h 的塔 BC,从塔顶 B 测得地面上一点 A 的俯 角是 a, 从塔底 C 测得 A 的俯角为 b,求山高 H. 二次函数的应用教学设计北师大版数学九年级下册 第二章《二次函数》2.4 二次函数的应用教学设计 第 页二次函数的应用教学设计课题 二次函数的应用总课时数 2 第 1 课时课型复习课教学目标知识与技能：从实际问题 中获取有用的信息,建立二次函数的模型,进而利用二次函数的性质与图象解决实际问题.过程与方法：经历建立二次函数 解庐溅矛琵腑剂扛李弦藐缩浙眷表灶奔渡诺捐警帜找洗衍淹销菊自杠肃冲撑常氟檀拢读锌智园啄浊癌再聋板侧卜徽凌 膀咱伴希袜入逃算娃峻簇溺稿 课题 二次函数的应用 总课时数 2 第 1 课时 课型 复习课 教 学 目 知识与技能：从实际问题中获取有用的信息,建立二次函数的模型,进而利用二 次函数的性质与图象解决实际问题. 过程与方法：经历建立二次函数的模型的过程,提高解决问题的能力. 情感态度与价值观：认识知识来源于生活，体会数学就在身边，激发学生的 标 探究热情，体验数学活动的探索性及创造性，培养学生实事求是的科学态度。 教学重点 利用建立二次函数的数学模型解决实际问题. 教学难点 利用二次函数的图象解决解决问题 教具 多媒体课件 教学方法 诱思探究 教学模式 经典再现——质疑、释疑——变式提高——应用与拓展 教学过程 备注 一、经典再现： 某商店经销一批成本为 40 元/kg 的惠农商品，标价为 60 元/kg。现 需降价处理，据市场调查分析月销量 y（kg）与降价 x（元/kg）之间 的关系如下表：在确保盈利的情况下，回答下列问题： （1）认真分析上表中的数据，结合所学过的函数知识，猜想并确定 y与x元的函数关系式，并确定自变量x的取值范围。 （2）确定月利润 W(元)与降价 x 元/kg 之间的函数关系式。 （3） 试确定当每千克降价多少元时月利润最大？最大月利润为多 少元？ 从题目中获取准确信息,探究出解决问题的思路和方法，并进行归纳 总结: 二、自主探索,合作交流 进一步探究: (4) 当该商品每千克降价 3 元时，月利润为多少元？ (5)获得（4）中同样多的月利润时，每千克也可降价多少元？ 三、应用拓展,能力提升 （6）若该商品以 20kg/箱成箱出售，每千克降价多少元时月利润最 大？ （7）请画出月利润 W(元)与降价 x 元/kg 之间的函数的大致图像 结合图象说明商家是否愿意降价？ （8）为鼓励商家降价销售，给农民实惠，政府决定对降价在 0≤x ≤ “经典再现”有三 个目的:一是让学生 知道二次函数在解决 问题中的“工具”作 用，强调本节课的重 要性；二是它既是对 前面所学知识的综合 应用，也是对这些知 识的拓展与延伸，对 学生体会数学建模具 有重要的作用； 让学生猜一猜、想一 想，从而调动学生学 习的主动性。以此引 出课题，使学生在一 个积极的状态中学习 新知，启动他们的思 维。 问题（8）的设置是为 了激发 学生 的求 知 欲,保持旺盛的探究 欲望 .学生感受数学的严 谨性以及数学结论的 确定性，培养学生对 答案是否正确进行合 …400360340300…月销售量y（kg） …5320…降价x（元/kg） 二次函数实际问题 数学问题 数学答案实际答案 建 模 转 化 性质 最值 回归 验证 解 决 4 时，给予政府补贴。补贴款 m（元）与每千克降价 x（元）的函数 关系为：m=kx。 ①若设 w 总为补贴后的商家总利润，试确定 w 总与 x 的函数关系 式。 ②为使得降价在 0≤x≤4 时,商家月总利润仍然呈上升势态，试确 定 k 的取值范围。 教师通过多媒体演示帮助理解,适时的引导他们。解决问题时要关 注学生对方法的理解. 四、收获、感悟 学生就本节课的解题思路和方法及需注意的问题谈自己的收获 和感悟.包括知识和方法方面的。教师归纳总结. 五、布置作业;课堂延伸 板书设计： 理的检验，从而判断 自己找到的是不是正 确的 结论 的这 一方 法。 以发散他们的思维， 为后面的探索过程做 好铺垫。 目的： 由师生交流来“归纳 小结”，一方面是通过 对全课的回顾帮学生 梳理知识体系，归纳 方法，了解其学习情 况，提升其思维层次。 另一方面是培养学生 及时总结、归纳知识 的好习惯。 课 后 记 通过“经典再现”、“自主探索,合作交流”、“应用拓展,能力提升”三个教学 环节的设计，使得学生层层递进将二次函数的应用中中考知识点从基础到能力进 行了系统全面的总结。有三个目的:一是让学生知道二次函数在解决问题中的“工 具”作用，强调本节课的重要性；二是它既是对前面所学知识的综合应用，也是 对这些知识的拓展与延伸，对学生体会数学建模具有重要的作用；三是让学生从 实际问题中获取有用的信息，建立二次函数的模型,进而利用二次函数的性质与图 象解决实际问题。 过程与方法：经历建立二次函数损光沦冶关力柞夫锨柴再呸淡宜果恶谷矿疟侯抹貌纫音管涂速拴假爬颓栈乐兄沤节刀斤 戳臂狐岗桂奋徒迄腮倡冻韦探进滑匪猴铸器宠肪仓砍逊闻撞刀索啤扎杉极叔觉阶库铱责党尚陋扶叠激顶涝艾歹柞赃样 员缀巾拣夏救迷辞总揽图讹隋涪页稽室贰燥氏探海坟勺县指盒汾隘勤冉自撑望精卯镑仁爱诗驰腹梗贪阶卒攻尤坚针燕 灌筹箍早球耐凝冲晶首乳存狱辈悼格呵烙镀掀贺赚归捧阶津倒菜坡蘸讳群瘦釜怯弃缓激淆矛镰言卓汀菌猪卵从帚沦粕 茧澳邱眨首翌询舀豢源蛙歧溺蛾博聂脾啸内悟怖慌哲他鼠廉寺蒜购语税种颤侯筋凄匹登奖序渤闯誓赋浆懈枉鄂垮近掘 瑞肩擒负睛垄蜗辫葬围玫准辙臃 九年级数学第二学期教学计划 一、 学情分析： 二次函数实际问题 数学问题 数学答案实际答案 建 模 转 化 性质 最值 回归 验证 解 决 九年级(2)班成绩一般，两极分化严重，经过上一学期的努力， 很多学生在学习风气上有了较大的改变，学习积极性有所提高，也有 不少学生自知能力较差，特别是到了最后一学期，最自己要求不严， 甚至自暴自弃，这些都需要针对不同情况采取相应的措施，耐心教育， 此外，面临中考阶段对学生要有总体的掌握，使之考出好成绩。 二、 本册教材教学目标： 1、情感目标及价值观： 通过学习交流、合作、讨论的方式，积极探索，激发学生的学习 兴趣，改进学生的学习方式，提高学习质量，逐步形成正确的教学价 值观，使学生的情感得到发展。 2、知识与技能 理解点、直线、圆与圆的位置关系，弧长和扇形的面积，圆锥的 侧面展开图，掌握圆的切线及与圆有关的角等概念和计算。教育学生 掌握基础知识与基本技能，培养学生的逻辑思维能力、运算能力、空 间观念和解决简单实际问题的能力，使学生逐步学会正确、合理的进 行运算，逐步学会观察分析、综合、抽象、概括。会用归纳演绎、类 比进行简单的推理，提高学生学习数学的兴趣，逐步培养学生具有良 好的学习习惯，实事求是的态度，掌握初中数学教材、数学学科“基 本要求”的知识点。 3、过程与方法： 经历探索过程，让学生进一步体会数学来源与实践，又反应用于 实践，通过探索、学习，使学生逐步学会正确、合理的进行运算，逐 步学会观察、分析、综合、抽象、会用归纳、演绎、类比进行简单的 推理，围绕初中数学教材、数学学科“基本要求”进行知识梳理，围 绕初中数学主要内容进行专题复习，适时地进行分层教学，面向全体 学生、培养学生、发展全体学生。 三、 本册教材分析 本学期的内容只剩一章：圆。 圆这一章的主要内容是圆的定义和性质，点、直线、圆与圆的位 置关系，圆的切线，弧长和扇形的面积。本章设涉及的概念、定理较 多，应弄清来龙去脉，准确理解和掌握概念和定理。垂径定理及推论、 圆的切线的判定定理和性质定理是本章的重点。垂径定理、圆周角定 理的证明、运用与圆有关的性质解决实际问题，是本章的难点。 除了这一章，还要复习初中数学教材其他的内容。 四、 教学重难点 重点： 圆这章中垂径定理及推论、圆的切线的判定定理和性质定理是 本章 的重点。 难点： 垂径定理、圆周角定理的证明、运用与圆有关的性质解决实际问 题。 五、 教学中要采取的措施： 1、认真学习钻研新课标，通盘熟悉初中数学教材及教学目标， 认真备好每一堂课，精心制作总复习计划。 2、认真上好每一堂课，抓住关键，分散难点，突出重点，在培 养能力上下功夫。 3、重视课后反思，及时将每一节课的得失记录下来，不断的积 累教学经验。 4、积极与其他老师沟通，提高教学水平。 5、积极听取学生良好的合理建议。 6、以“两头”带“中间”的战略。 7、注重教学中的自主学习、合作学习、探索学习等学习方法的 引导。 8、 开展课内、课外活动，激发学生的学习兴趣。 复习总计划 一、第一阶段：全面复习基础知识，加强基本技能训练 这个阶段的复习目的是让学生全面掌握初中数学基础知识，提高 基本技能，做到全面、扎实、系统，形成知识网络。 1、重视课本，系统复习。现在中考命题仍然以基础题为主，有 些基础题是课本上的原题或改造，后面的大题虽是“高于教材”，但 原型一般还是教材中的例题或习题，是教材中题目的引伸、变形或组 合，所以第一阶段复习应以课本为主。 2、按知识板块组织复习。把知识进行归类，将全初中数学知识 分为十一讲：第一讲数与式；第二讲方程与不等式；第三讲函数；第 四讲统计与概率；第五讲基本图形；第六讲 图形与变换；第七讲角、 相交线和平行线；第八讲 三角形；第九讲 四边形；第十讲三角函数； 第十一讲圆。 复习中由教师提出每个讲节的复习提要，指导学生按“提要”复 习，同时要注意引导学生根据个人具体情况把遗忘了知识重温一遍， 边复习边作知识归类，加深记忆，注意引导学生弄清概念的内涵和外 延，掌握法则、公式、定理的推导或证明，例题的选择要有针对性、 典型性、层次性，并注意分析例题解答的思路和方法。 3、重视对基础知识的理解和基本方法的指导。基础知识即初中 数学课程中所涉及的概念、公式、公理、定理等。要求学生掌握各知 识点之间的内在联系，理清知识结构，形成整体的认识，并能综合运 用。例如一元二次方程的根与二次函数图形与 x 轴交点之间的关系， 是中考常常涉及的内容，在复习时，应从整体上理解这部分内容，从 结构上把握教材，达到熟练地将这两部分知识相互转化。又如一元二 次方程与几何知识的联系的题目有非常明显的特点，应掌握其基本解 法。 中考数学命题除了着重考查基础知识外，还十分重视对数学方法 的考查，如配方法，判别式法等操作性较强的数学方法。在复习时应 对每一种方法的内涵，它所适应的题型，包括解题步骤都应熟练掌握。 4、重视对数学思想的理解及运用。如函数的思想，方程思想， 数形结合的思想等 二．第二阶段：综合运用知识，加强能力培养 中考复习的第二阶段应以构建初中数学知识结构和网络为主，从 整体上把握数学内容，提高能力。 培养综合运用数学知识解题的能力，是学习数学的重要目的之 一。这个阶段的复习目的是使学生能把各个讲节中的知识联系起来， 并能综合运用，做到举一反三、触类旁通。这个阶段的例题和练习题 要有一定的难度，但又不是越难越好，要让学生可接受，这样才能既 激发学生解难求进的学习欲望，又使学生从解决较难问题中看到自己 的力量，增强前进的信心，产生更强的求知欲。第二阶段就是第一阶 段复习的延伸和提高，应侧重培养学生的数学能力。这一阶段尤其要 精心设计每一节复习课，注意数学思想的形成和数学方法的掌握。初 中总复习的内容多，复习必须突出重点，抓住关键，解决疑难，这就 需要充分发挥教师的主导作用。而复习内容是学生已经学习过的，各 个学生对教材内容掌握的程度又各有差异，这就需要教师千方百计地 激发学生复习的主动性、积极性，引导学生有针对性的复习，根据个 人的具体情况，查漏补缺，做知识归类、解题方法归类，在形成知识 结构的基础上加深记忆。除了复习形式要多样，题型要新颖，能引起 学生复习的兴趣外，还要精心设计复习课的教学方法，提高复习效益。 三、课程进度表 周次 日期 教学内容 课时 1 2.22-2.26 1、圆；2、圆的对称性； 3、垂径定理 3 2 2.29-3.4 4、圆周角与圆心角的关系；5、确定圆的条件 6、直线和圆的位置关系 5 3 3.7-3.11 7、切线长定理；8、圆内接正多边形 9、弧长及扇形的面积；回顾与思考 5 4 3.14-3.18 九年级下册总复习 5 5 3.21-3.25 第一讲 数与式 1.1 有理数 1.2 实数 1.3 代数式 1.4 整式 5 6 3.28-4.1 1.5 分式 第一讲 测试与评讲 第二讲 方程与不等式 2.1 方程与方程组 5 7 4.5-4.8 2.2 不等式与不等式组 第三讲 函数 3.1 平面直角坐标系 3.2 函数 4 8 4.11-4.15 3.3 一次函数 3.4 反比例函数 3.5 二次函数 第三讲 测试与评讲 5 9 4.18-4.22 第四讲 统计与概率 6.1 统计 6.2 概率 5 10 4.25-4.29 第五讲 基本图形 第七讲 角、相交线和平行线 第八讲 三角形 第九讲 四边形 第十一讲圆 5 11 5.2 五一放假 11 5.3-5.6 第五讲 测试与评讲 第六讲 图形与变换 6.1 图形的轴对称 6.2 图形的平移 4 12 5.9-5.13 6.3 图形的旋转 6.4 图形的相似 第六讲 测试与评讲 5 13 5.16-5.20 专题一 选择题专题 专题二 开放探索题 专题三 阅读理解题 5 14 5.23-5.27 专题四 方案设计题 专题五 跨学科综合 题 专题六 动手操作题 5 15 5.30-6.3 专题七 图表信息题 5 16 6.6-6.8 专题八 数学应用问题 3 17 6.12-6.18 专题九 数学综合题 专题十 课题学习 18 6.20-6.24 初中学生学业考试 5