九年级数学下册第三章圆3圆周角和圆心角的关系第2课时习题课件北师大版 30页

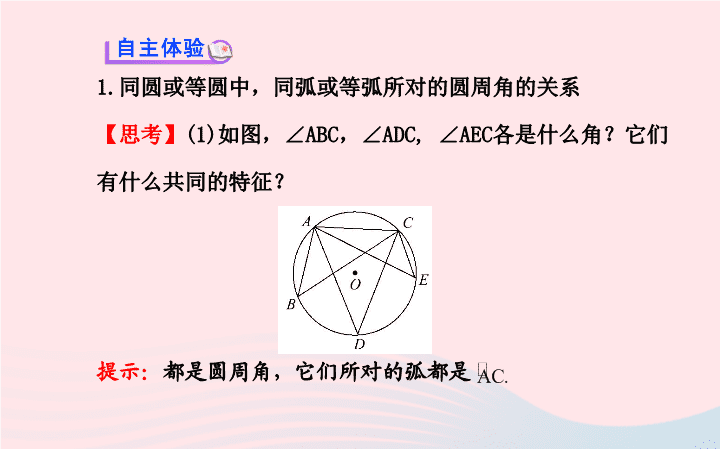
3 圆周角和圆心角的关系 第 2 课时 1. 圆周角定理的两个推论及其应用 .( 重点、难点 ) 2. 理解两个推论的“题设”和“结论” .( 难点 ) 1. 同圆或等圆中，同弧或等弧所对的圆周角的关系 【 思考 】 (1) 如图，∠ ABC ，∠ ADC, ∠AEC 各是什么角？它们 有什么共同的特征？ 提示： 都是圆周角，它们所对的弧都是 (2)∠ABC ，∠ ADC, ∠AEC 的大小有什么关系？为什么？ 提示： 相等 . 连接 AO,CO 【 总结 】 在同圆或等圆中，同弧或 _____ 所对的圆周角 _____ ， 都等于它们所对的弧所对 _______ 的一半 . 等弧 相等 圆心角 2. 直径与 90° 的圆周角的关系 (1) 直径所对的圆周角是 _____. (2)90° 的圆周角所对的弦是 _____. 所对的弧是 _____. 直角 直径 半圆 ( 打“√”或“ ×”) (1) 等弧所对的圆周角相等 . ( ) (2) 同圆中，等弦所对的圆周角相等 .( ) (3) 同弧所对的圆周角相等 .( ) (4) 相等的圆周角所对的弧也相等 .( ) (5)90 ° 的角所对的弦是直径 .( ) √ × √ × × 知识点 1 同圆或等圆中，同弧或等弧所对的圆周角的关系 【 例 1】 (2012· 梅州中考 ) 如图， AC 是⊙ O 的直径，弦 BD 交 AC 于 点 E. (1) 求证：△ ADE∽△BCE. (2) 如果 AD 2 =AE · AC ，求证： CD=CB. 【 解题探究 】 1. 要证△ ADE∽△BCE, 由已知可以得到哪些角相 等？为什么？ 提示： (1)∠A=∠B. ∵∠A,∠B 所对的弧都是 ∴∠ A=∠B. (2)∠AED=∠BEC( 对顶角相等 ) 2. 由 AD 2 =AE · AC 可以得到什么样的比例式？ 提示： ( 答案不惟一，正确即可 ) 3. 由 2 中的比例式，可以得到△ ADE 与△ ACD 有什么关系？为什 么？ 提示： △ ADE∽△ACD. ∵∠A=∠A, ∴△ADE∽△ACD. 4. 由 3 可得∠ DEA =_____, 故 CD=CB. 90 ° 【 总结提升 】 同弧或等弧所对的圆周角相等的运用 根据 “ 同弧或等弧所对的圆周角相等；在同圆或等圆中 , 相等的圆周角所对的弧相等 ” , 由弧找角 , 由角找弧 , 是证明弧相等或角相等常用的思维方法 , 构造同弧或等弧所对的圆周角是常作的辅助线 . 知识点 2 直径与 90° 的圆周角的关系 【 例 2】 已知 CO ， CB 是⊙ O′ 的弦，⊙ O′ 与直角坐标系的 x 轴、 y 轴分别交于点 B 、点 A ，若∠ COB=45° ，∠ OBC=75° ，点 A(0,2), 求⊙ O′ 的直径 . 【 思路点拨 】 作辅助线 AB ，可得 Rt △ AOB ，由已知可得 ∠ OCB=60 ° , 进而求得 Rt △ AOB 中∠ OAB=60 ° , 则直径 AB 可求 . 【 自主解答 】 连接 AB,∵CO 为⊙ O′ 的弦， ∴ O 为⊙ O′ 上的一点 . ∵∠AOB=90° ， ∴ AB 为⊙ O′ 的直径 . ∵∠BOC=45° ，∠ OBC=75° ， ∴∠ OAB=∠OCB=180°-45°-75°=60° ． ∴∠ ABO=90°-60°=30°. ∵A 点坐标为 (0 ， 2) ，∴ AO=2 ． 在 Rt △ AOB 中 ， AB=2AO=4. 【 总结提升 】 直径和圆周角 1. 在圆中 , 若有直径时 , 构造直径所对的圆周角得直角是常用的添加辅助线的方法；条件中有 90° 的圆周角时 , 一般用该圆周角所对的弦是直径 . 2. 在解题时注意勾股定理、垂径定理、以及三角形相似的应用 . 题组一： 同圆或等圆中，同弧或等弧所对的圆周角的关系 1. 如图，∠ 1 ，∠ 2 ，∠ 3 ，∠ 4 的大小关系是 ( ) A.∠4 ＜∠ 1 ＜∠ 2 ＜∠ 3 B.∠4 ＜∠ 1=∠3 ＜∠ 2 C.∠4 ＜∠ 1 ＜∠ 3 ＜∠ 2 D.∠4 ＜∠ 1 ＜∠ 3=∠2 【 解析 】 选 B. 由圆周角定理可知∠ 1= ∠ 3= ∠ AMB= ∠ ACB ，由三角形的外角性质可知∠ 4 ＜∠ ACB ，∠ AMB ＜∠ 2 ，所以∠ 4 ＜∠ 1= ∠ 3 ＜∠ 2. 2. 如图所示，⊙ O 的两弦 AB ， CD 交于点 P ，连接 AC ， BD ，若 S △ACP ∶S △DBP =16∶9 ，则 AC∶BD=___________. 【 解析 】 由图可知∠ C=∠B ，∠ A=∠D ，∴△ ACP∽△DBP, ∴AC∶BD=4∶3. 答案： 4 ∶ 3 3. 如图 ,A,P,B,C 是半径为 8 的☉ O 上的四点 , 且满足∠ BAC=∠APC=60°, (1) 求证 :△ABC 是等边三角形 . (2) 求圆心 O 到 BC 的距离 OD. 【 解析 】 (1)∵∠ABC=∠APC, 又∵∠ BAC=∠APC=60°, ∴∠ABC=∠BAC=60°,∠ACB=60°, ∴∠ABC=∠BAC=∠ACB=60°, ∴△ABC 是等边三角形 . (2) 连接 OB, 如图 , 则易得∠ OBD=30°,∠ODB=90°, 题组二： 直径与 90° 的圆周角的关系 1.(2013· 宜昌中考 ) 如图， DC 是⊙ O 的直径，弦 AB⊥CD 于 F ，连接 BC ， DB ，则下列结论错误的是 ( ) 【 解析 】 选 C.∵DC 是⊙ O 的直径，∴∠ DBC=90° ， 又∵ AB⊥CD 于 F ，∴ AF=BF ， ∴ A ， B ， D 正确 . 2.(2013· 日照中考 ) 如图，在△ ABC 中，以 BC 为直径的圆分别交边 AC ， AB 于 D ， E 两点，连接 BD ， DE ．若 BD 平分∠ ABC ，则下列结论不一定成立的是 ( ) A.BD⊥AC B.AC 2 =2AB·AE C.△ADE 是等腰三角形 D.BC ＝ 2AD 【 解析 】 选 D.∵BC 为圆的直径，∴∠ BDC=90° ，∴ BD⊥AC ，故 A 正确；∵ BD 平分∠ ABC ，∴∠ ABD=∠CBD ， BD 为公共边，∴△ ABD≌△CBD ，∴ AD=CD ，∠ A=∠C ，又∵∠ AED=∠C ，∴∠ AED=∠A ，∴△ ADE 是等腰三角形，故 C 正确 .∵∠A=∠A ， ∠ AED=∠C ， ∴△ AED ∽△ ACB ， 即 AE · AB=AC · AD ， 又 即 AC 2 =2AB · AE ，故 B 正确 . BC 不一定等于 AC ，故 D 不一定成立 . 3.(2013· 佛山中考 ) 图中圆心角∠ AOB=30° ，弦 CA∥OB ，延长 CO 与圆交于点 D ，则∠ BOD=______ ． 【 解析 】 ∵OA=OC,∴∠OAC=∠OCA,∵∠AOB=30° ， CA∥OB,∴∠OAC=∠OCA=∠AOB=30° ，又 CA∥OB,∴∠BOD= ∠OCA=30°. 答案： 30 ° 4.(2013· 淄博中考 ) 如图， AB 是⊙ O 的直径， BD=4 ，则 sin∠ECB=______ ． 【 解析 】 连接 AD ，∵ AB 是⊙ O 的直径， ∴∠ ADB=90° ，∠ DAE=∠DBA. ∵AB=5 ， BD=4 ，∴ AD=3. 设 CD=3k ， AC=5k ，则 AD=4k ， 答案： 5.(2013· 黔西南州中考 ) 如图所示， AB 是⊙ O 的直径，弦 CD⊥AB 于点 E ，点 P 在⊙ O 上，∠ 1=∠C. (1) 求证： CB∥PD. (2) 若 BC=3 ， 求⊙ O 的直径 . 【 解析 】 (1)∵∠D=∠1,∠1=∠C,∴∠D=∠C,∴CB∥PD. (2) 连接 AC ，如图， ∵ AB 是⊙ O 的直径，弦 CD⊥AB 于点 E ， 又∵ AB 为直径，∴∠ ACB=90° ， ∴ AB=5 ，即⊙ O 的直径为 5. 【 想一想错在哪？ 】 已知 A,B,C 三点都在☉ O 上 , 若☉ O 的半径　　　　　为 4cm, 弦 BC 为 4cm, 求∠ A 的度数 . 提示 : 本题只考虑了圆心 O 在△ ABC 内的情况 , 没考虑圆心 O 在△ ABC 外的情况 .