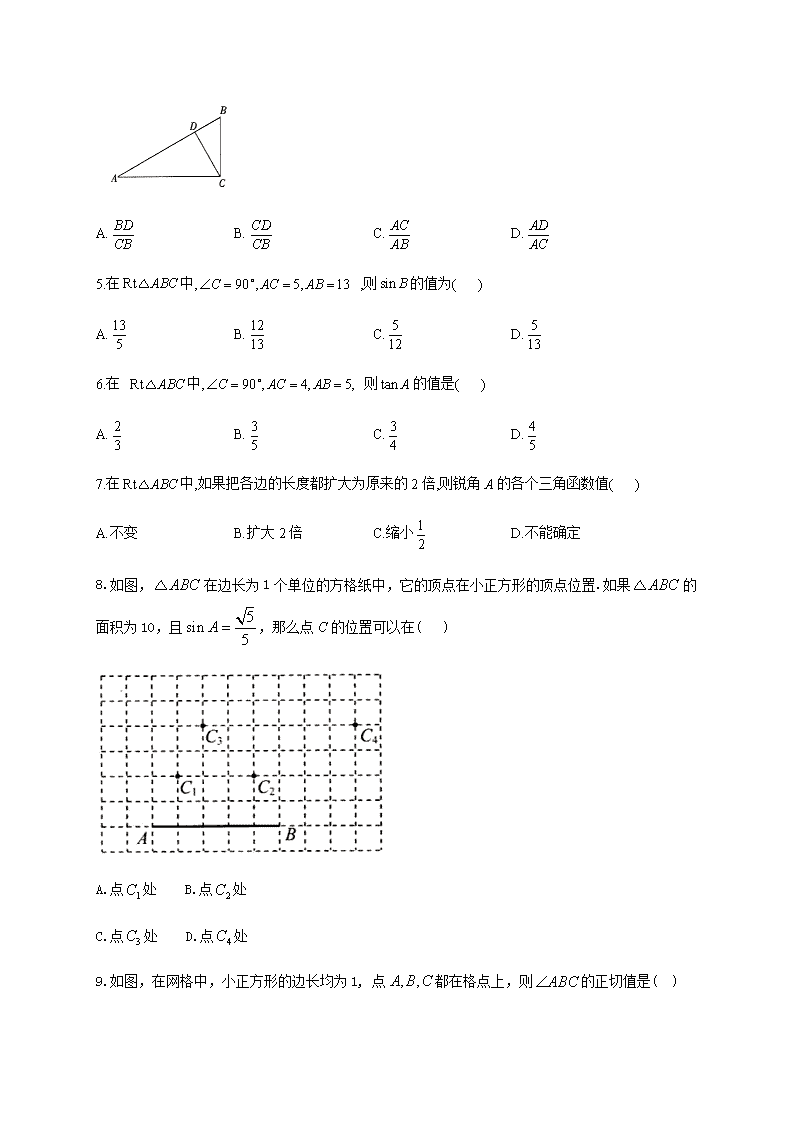北师大版（2012）九年级下册数学随堂小练：1锐角三角函数 7页

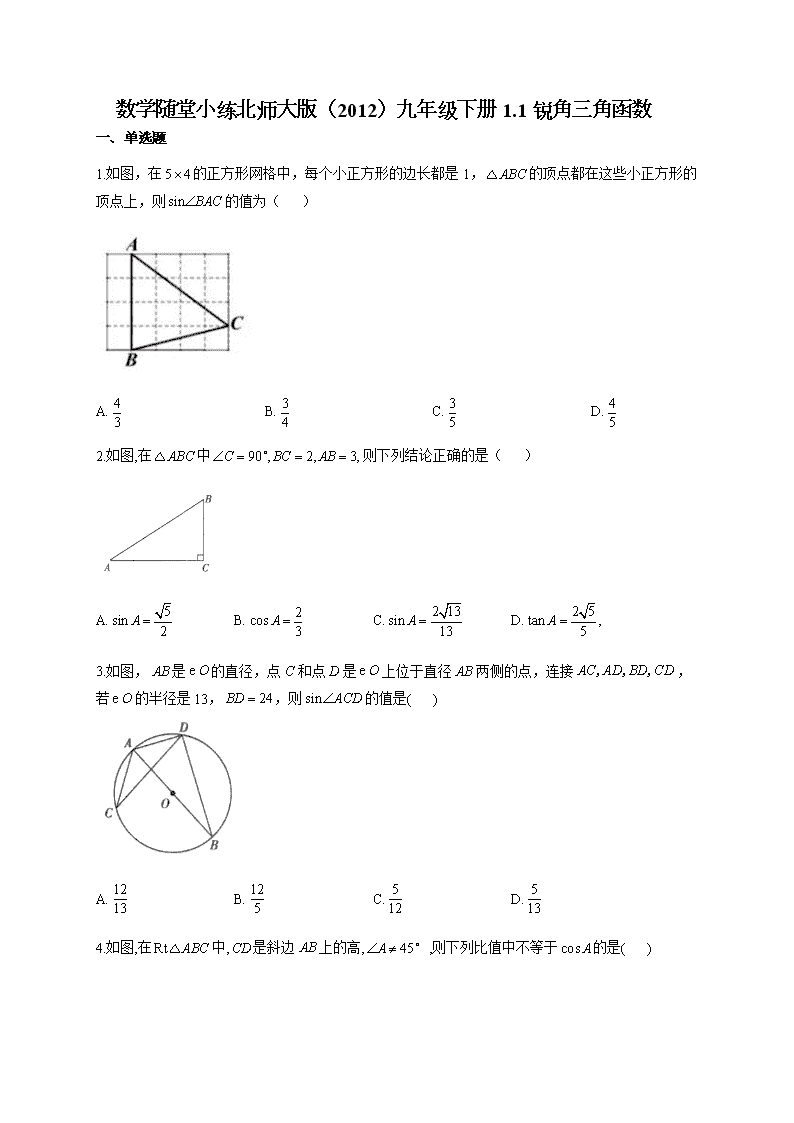
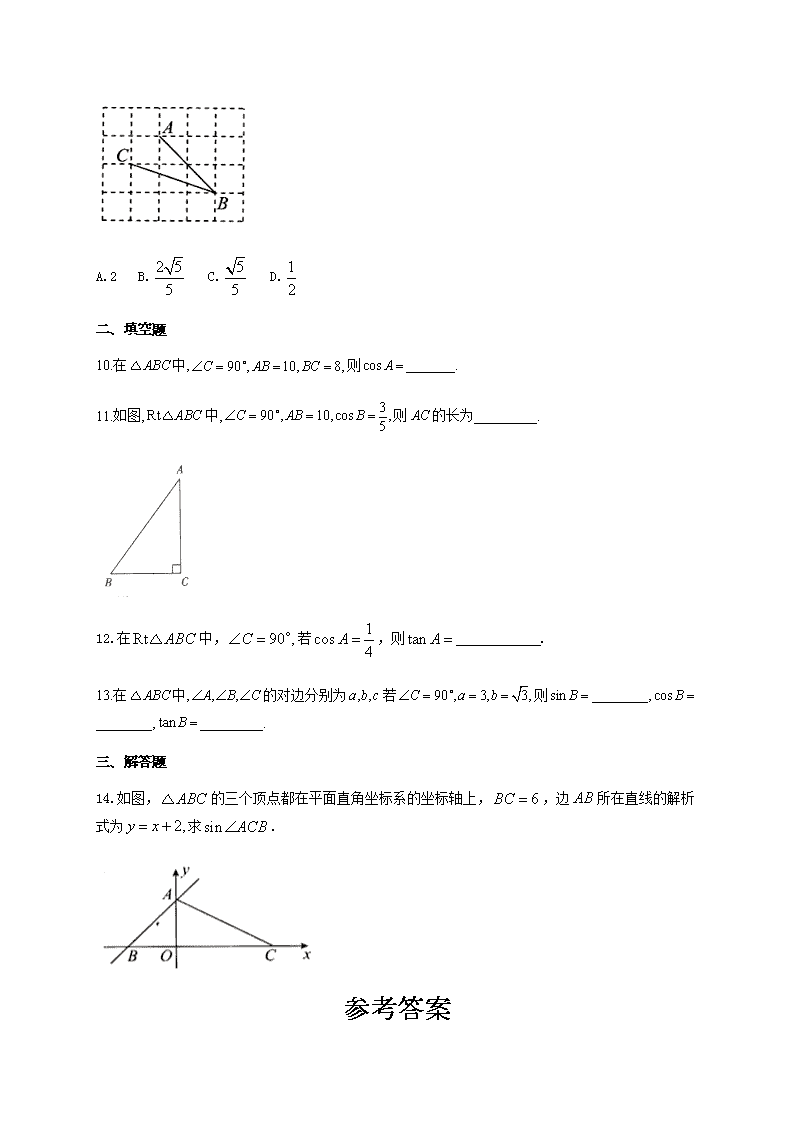
数学随堂小练北师大版（2012）九年级下册 1.1 锐角三角函数 一、单选题 1.如图，在 5 4 的正方形网格中，每个小正方形的边长都是 1， ABC△ 的顶点都在这些小正方形的 顶点上，则 sin BAC 的值为（ ） A. 4 3 B. 3 4 C. 3 5 D. 4 5 2.如图,在 ABC△ 中 90 , 2, 3,C BC AB   ° 则下列结论正确的是（ ） A. 5sin 2 A  B. 2cos 3 A  C. 2 13sin 13 A  D. 2 5tan , 5 A  3.如图， AB是 Oe 的直径，点 C和点 D是 Oe 上位于直径 AB两侧的点，连接 AC AD BD CD, , , ， 若 Oe 的半径是 13， 24BD  ，则 sin ACD 的值是( ) A. 12  13 B. 12 5 C. 5 12 D. 5 13 4.如图,在Rt ABC△ 中,CD是斜边 AB上的高, 45A  ° ,则下列比值中不等于 cos A的是( ) A. BD CB B. CD CB C. AC AB D. AD AC 5.在Rt ABC△ 中, 90 , 5, 13C AC AB   ° ,则 sin B的值为( ) A.13 5 B.12 13 C. 5 12 D. 5 13 6.在 Rt ABC△ 中, 90 , 4, 5,C AC AB   ° 则 tan A的值是( ) A. 2 3 B. 3 5 C. 3 4 D. 4 5 7.在Rt ABC△ 中,如果把各边的长度都扩大为原来的 2倍,则锐角 A的各个三角函数值( ) A.不变 B.扩大 2倍 C.缩小 1 2 D.不能确定 8.如图， ABC△ 在边长为 1个单位的方格纸中，它的顶点在小正方形的顶点位置.如果 ABC△ 的 面积为 10，且 5sin 5 A  ，那么点 C的位置可以在( ) A.点 1C 处 B.点 2C 处 C.点 3C 处 D.点 4C 处 9.如图，在网格中，小正方形的边长均为 1, 点 , ,A B C都在格点上，则 ABC 的正切值是( ) A.2 B. 2 5 5 C. 5 5 D. 1 2 二、填空题 10.在 ABC△ 中, 90 , 10, 8,C AB BC   ° 则 cos A  _______. 11.如图,Rt ABC△ 中, 390 , 10,cos , 5 C AB B   ° 则 AC 的长为_________. 12.在Rt ABC△ 中， 90 ,C  ° 若 1cos 4 A  ，则 tan A  . 13.在 ABC△ 中, , ,A B C   的对边分别为 , ,a b c若 90 , 3, 3,C a b   ° 则 sin B  ________, cosB  ________, tan B  _________. 三、解答题 14.如图， ABC△ 的三个顶点都在平面直角坐标系的坐标轴上， 6BC  ，边 AB所在直线的解析 式为 2,y x  求 sin ACB . 参考答案 1.答案：D 如图，过 C作CD AB 于 D，则 90ADC  ， 2 2 2 23 4 5AC AD CD      ． 4sin 5 CDBAC AC     ． 故选 D. 2.答案：D 在 ABC△ 中, 90 , 2, 3,C BC AB   ° 2 2 2 23 2 5.AC AB BC      2 5 2 2 5sin ,cos , tan , 3 3 55 A A A     只有选项 D正确.故选 D. 3.答案：D ABQ 是直径， 90ADB  ， OQe 的半径是 13， 2 13 26AB    ， 由勾股定理得 2 2 10AD AB BD   ， 10 5sin 26 13 ADB AB     . ACD B  Q ， 5sin sin 13 ACD B    ，故选 D. 4.答案：A CD 是斜边 AB上的 高, 90 , 90BDC ADC B DCB     ° °. 90 , ,ACB A DCB    ° cos ,AC CD ADA AB CB AC     故选 A. 5.答案：D 在Rt ABC△ 中， 590 , 5, sin . 13 ACC AC B AB      ° 故选 D. 6.答案：C 在Rt ABC△ 中， 90 , 4, 5,C AC AB   ° 2 2 3BC AB AC    , 3tan , 4 BCA AC    故选 C. 7.答案：A 因为把 ABC△ 各边的长度都扩大为原来的 2倍所得的三角形与原三角形相似，所以锐角 A的度数不 变，所以锐角 A的 各个三角函数值不变.故选 A. 8.答案：D 如图， 5, 10, 4.ABCAB S DC    △ 5 5 4sin , , 5 5 DCA AC AC     4 5.AC  在 4Rt ADC△ 中， 2 2 4 44, 8, 8 4 4 5,DC AD AC      故选 D. 9.答案：D 如图，连接 AC，由勾股定理，得 2, 2 2, 10,AC AB BC   2 2 2 ,AC AB BC   ABC△ 为直角三角形， 1tan . 2 ACABC AB     C 10.答案： 3 5 由勾股定理得 2 2 2 210 8 6,AC AB BC     6 3cos . 10 5 ACA AB     11.答案：8 Rt ABC △ 中， 390 , 10,cos , 5 BCC AB B AB     ° 6,BC  由勾股定理得 2 2 2 210 6 8.AC AB BC     12.答案： 15 方法 1:由 1cos 4 A  知， 2 15sin 1 cos , 4 A A   sintan 15. cos AA A    方法 2:设 ,b x 则 4c x ，根据 2 2 2a b c  得 15 .a x 15tan 15.a xA b x     13.答案： 1 3 3; ; 2 2 3 在 ABC△ 中, 90 , 3, 3,C a b    ° 2 2 2 3.c a b    1 3 3 3sin ,cos , tan . 2 2 32 3 b a bB B B c c a         14.答案：解:直线 AB的解析式为 2,y x  当 0y  时， 2x   ;当 0x  时， 2.y  点  0,2A ，点 0( )2,B  ， 2, 2.OA OB   6, 6 2 4,BC OC BC OB       2 2 2 22 4 2 5,AC OA OC      2 5sin . 52 5 OAACB AC     