- 272.54 KB
- 2021-11-07 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
周滚动练(24.3~24.4)
(时间:60分钟 满分:100分)
一、选择题(每小题4分,共28分)
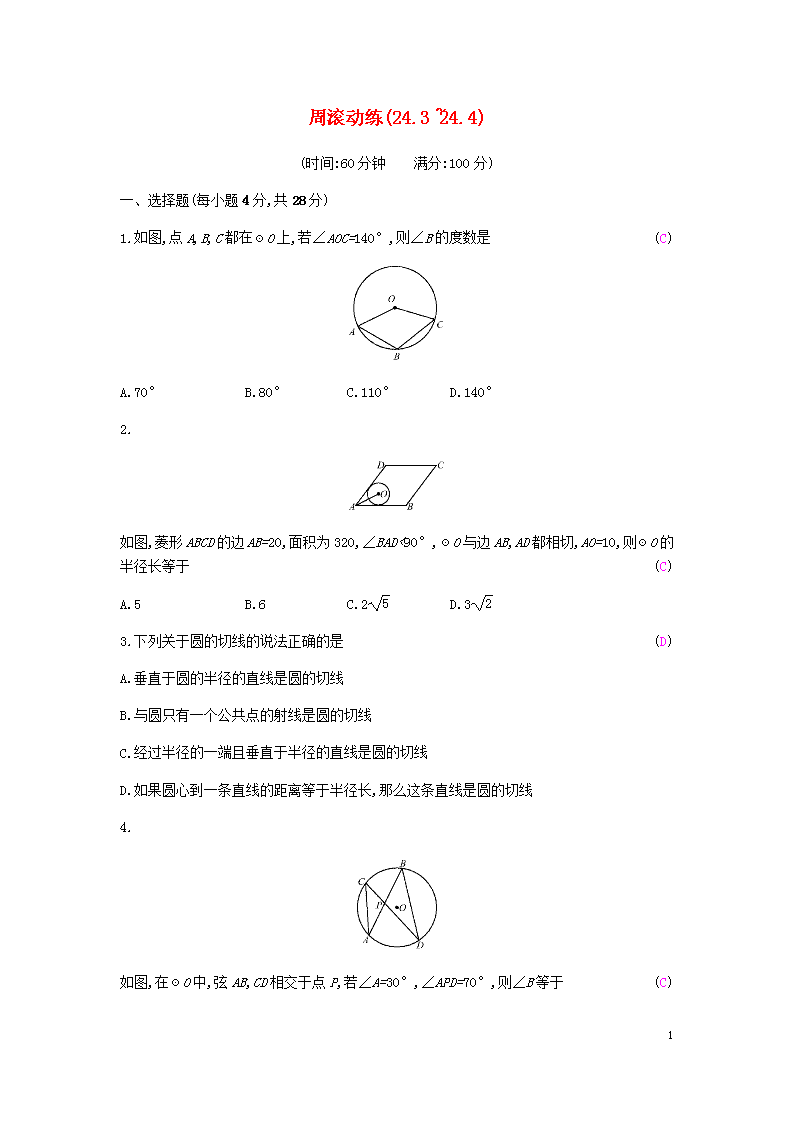
1.如图,点A,B,C都在☉O上,若∠AOC=140°,则∠B的度数是(C)
A.70° B.80° C.110° D.140°
2.
如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,☉O与边AB,AD都相切,AO=10,则☉O的半径长等于(C)
A.5 B.6 C.25 D.32
3.下列关于圆的切线的说法正确的是(D)
A.垂直于圆的半径的直线是圆的切线
B.与圆只有一个公共点的射线是圆的切线
C.经过半径的一端且垂直于半径的直线是圆的切线
D.如果圆心到一条直线的距离等于半径长,那么这条直线是圆的切线
4.
如图,在☉O中,弦AB,CD相交于点P,若∠A=30°,∠APD=70°,则∠B等于(C)
6
A.30° B.35°
C.40° D.50°
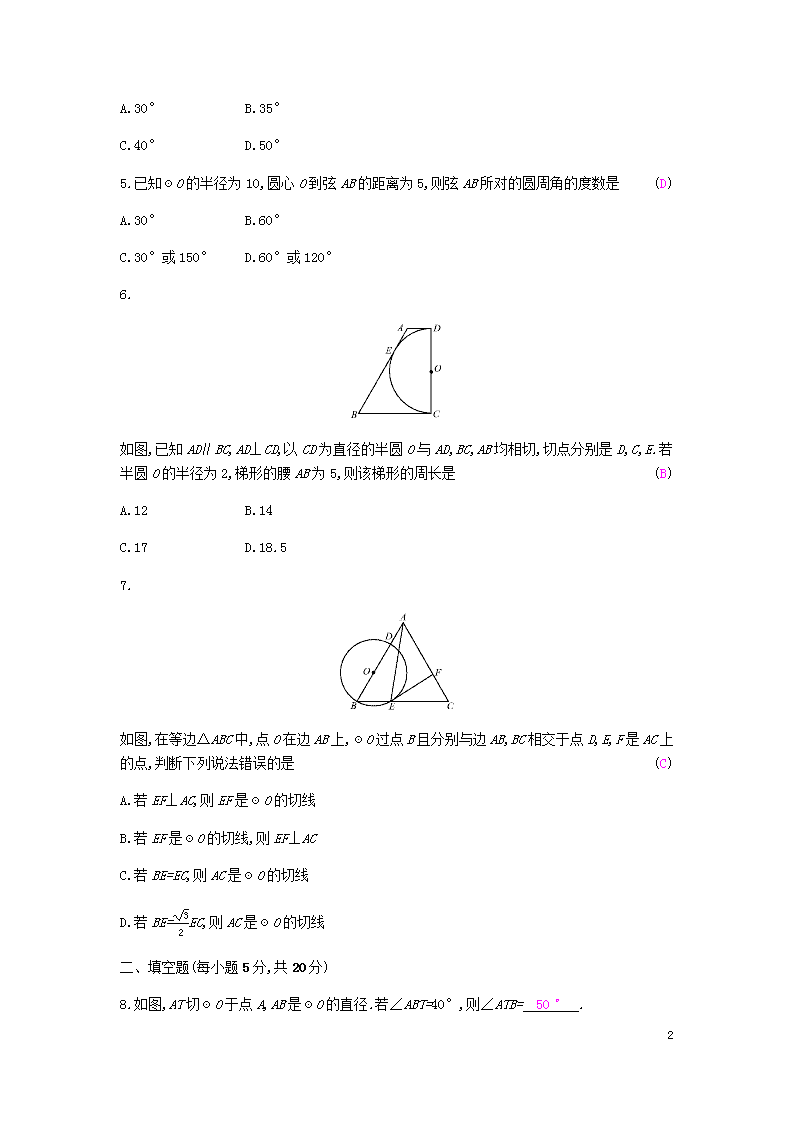
5.已知☉O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是(D)
A.30° B.60°
C.30°或150° D.60°或120°
6.
如图,已知AD∥BC,AD⊥CD,以CD为直径的半圆O与AD,BC,AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是(B)
A.12 B.14
C.17 D.18.5
7.
如图,在等边△ABC中,点O在边AB上,☉O过点B且分别与边AB,BC相交于点D,E,F是AC上的点,判断下列说法错误的是(C)
A.若EF⊥AC,则EF是☉O的切线
B.若EF是☉O的切线,则EF⊥AC
C.若BE=EC,则AC是☉O的切线
D.若BE=32EC,则AC是☉O的切线
二、填空题(每小题5分,共20分)
8.如图,AT切☉O于点A,AB是☉O的直径.若∠ABT=40°,则∠ATB= 50° .
6
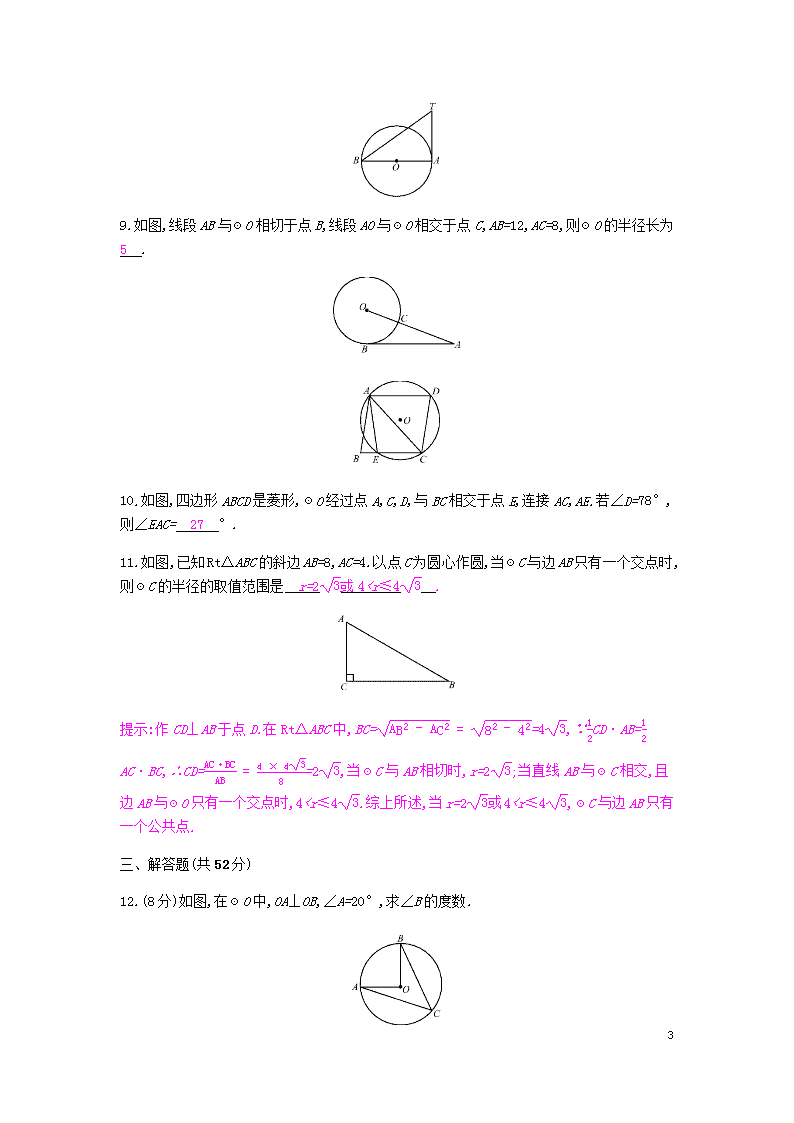
9.如图,线段AB与☉O相切于点B,线段AO与☉O相交于点C,AB=12,AC=8,则☉O的半径长为 5 .
10.如图,四边形ABCD是菱形,☉O经过点A,C,D,与BC相交于点E,连接AC,AE.若∠D=78°,则∠EAC= 27 °.
11.如图,已知Rt△ABC的斜边AB=8,AC=4.以点C为圆心作圆,当☉C与边AB只有一个交点时,则☉C的半径的取值范围是 r=23或40,∴x=23,∴☉O的半径为23.
16.(12分)如图,C是以AB为直径的☉O上一点,CD是☉O的切线,点D在AB的延长线上,作AE⊥CD于点E.
(1)求证:AC平分∠BAE;
(2)若AC=2CE=6,求☉O的半径;
(3)请探索:线段AD,BD,CD之间有何数量关系?并证明你的结论.
6
解:(1)连接OC.∵CD是☉O的切线,∴OC⊥CD,
∵AE⊥CD,∴OC∥AE,∴∠EAC=∠ACO,
∵OA=OC,∴∠CAO=∠ACO,∴∠EAC=∠CAO,即AC平分∠BAE.
(2)连接BC.∵AE⊥CE,AC=2CE=6,
∴sin ∠CAE=CEAC=12,∴∠CAE=30°,∴∠CAB=∠CAE=30°.∵AB是☉O的直径,∴∠ACB=90°,∴cos ∠CAB=ACAB=32,∴AB=43,∴☉O的半径是23.
(3)CD2=BD·AD.
理由:∵∠DCB+∠BCO=90°,∠ACO+∠BCO=90°,∴∠DCB=∠ACO,∴∠DCB=∠ACO=∠CAD,∵∠D=∠D,∴△BCD∽△CAD,
∴BDCD=CDAD,即CD2=BD·AD.
6
相关文档
- 九年级数学上册第二十四章圆24-1圆2021-11-063页
- 九年级数学上册第二十四章圆24-1圆2021-11-0615页
- 2008年中考数学分类真理练习21圆的2021-11-0613页
- 2018届二轮复习专题51圆的方程以及2021-06-2417页
- 高中数学必修2教案:4.2.1圆与圆的位置2021-06-223页
- 高考数学一轮复习第十章平面解析几2021-06-1915页
- 高中数学必修2教案:第四章 4_1_1圆2021-06-199页
- 高中数学必修2教案:4_1_1圆的标准方2021-06-175页
- 【数学】2019届一轮复习人教A版(文)92021-06-1621页
- 【数学】2020届一轮复习人教B版(理)2021-06-1610页