2018—2020年江苏省数学中考试题分类（8）——一次函数（含解析） 34页

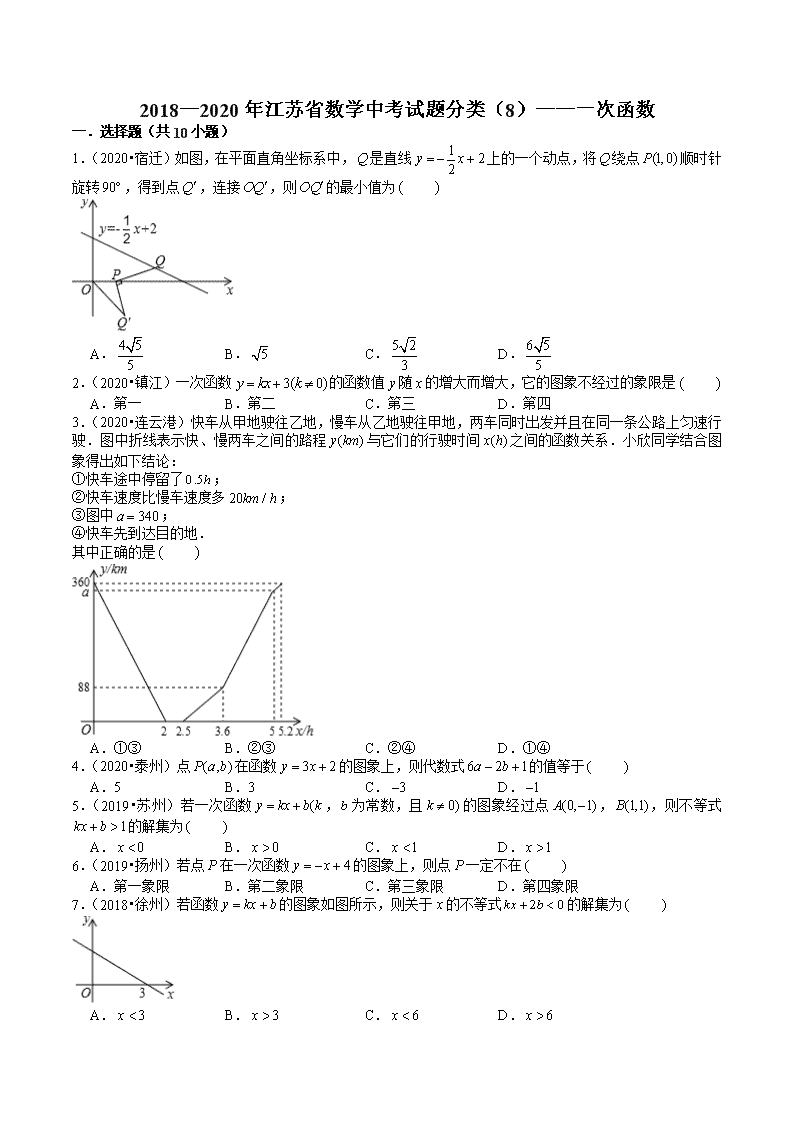
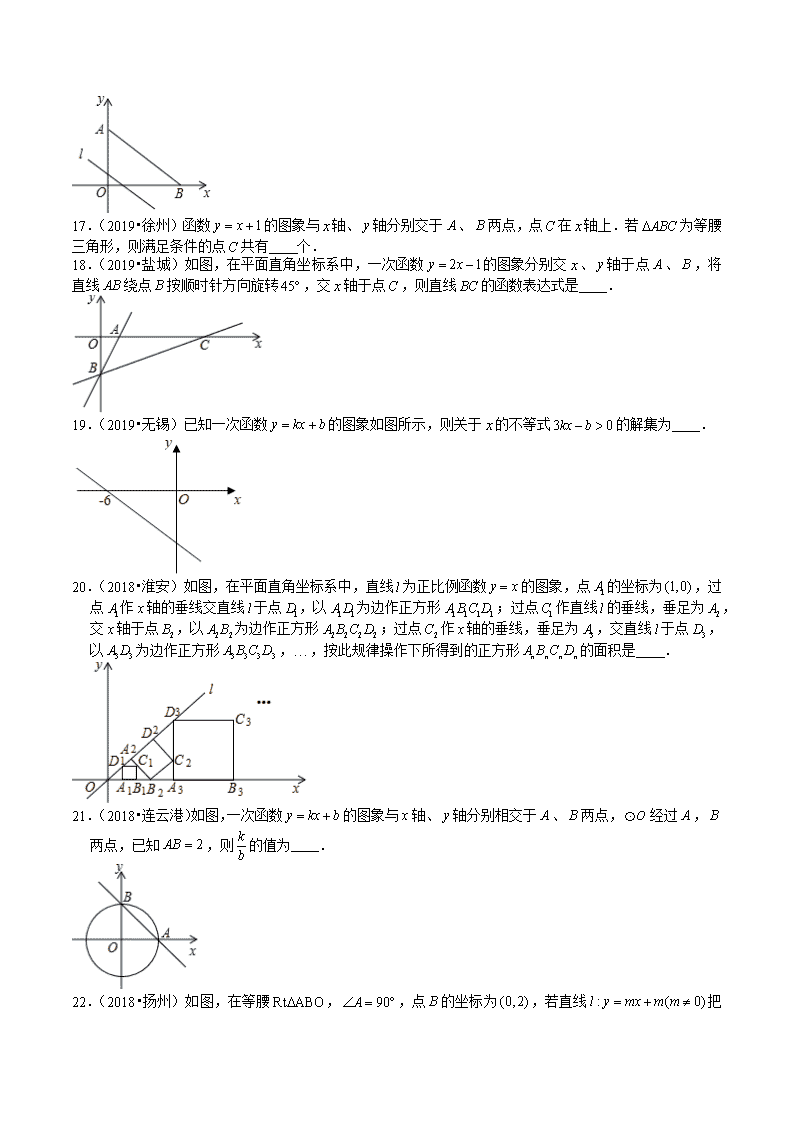
‎2018—2020年江苏省数学中考试题分类（8）——一次函数 一．选择题（共10小题）‎ ‎1．（2020•宿迁）如图，在平面直角坐标系中，是直线上的一个动点，将绕点顺时针旋转，得到点，连接，则的最小值为　　‎ A． B． C． D．‎ ‎2．（2020•镇江）一次函数的函数值随的增大而增大，它的图象不经过的象限是　　‎ A．第一 B．第二 C．第三 D．第四 ‎3．（2020•连云港）快车从甲地驶往乙地，慢车从乙地驶往甲地，两车同时出发并且在同一条公路上匀速行驶．图中折线表示快、慢两车之间的路程与它们的行驶时间之间的函数关系．小欣同学结合图象得出如下结论：‎ ‎①快车途中停留了；‎ ‎②快车速度比慢车速度多；‎ ‎③图中；‎ ‎④快车先到达目的地．‎ 其中正确的是　　‎ A．①③ B．②③ C．②④ D．①④‎ ‎4．（2020•泰州）点在函数的图象上，则代数式的值等于　　‎ A．5 B．3 C． D．‎ ‎5．（2019•苏州）若一次函数，为常数，且的图象经过点，，则不等式的解集为　　‎ A． B． C． D．‎ ‎6．（2019•扬州）若点在一次函数的图象上，则点一定不在　　‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎7．（2018•徐州）若函数的图象如图所示，则关于的不等式的解集为　　‎ A． B． C． D．‎ ‎8．（2018•常州）一个正比例函数的图象经过，则它的表达式为　　‎ A． B． C． D．‎ ‎9．（2018•泰州）如图，平面直角坐标系中，点的坐标为，轴，垂足为，点从原点出发向轴正方向运动，同时，点从点出发向点运动，当点到达点时，点、同时停止运动，若点与点的速度之比为，则下列说法正确的是　　‎ A．线段始终经过点 ‎ B．线段始终经过点 ‎ C．线段始终经过点 ‎ D．线段不可能始终经过某一定点 ‎10．（2018•宿迁）在平面直角坐标系中，过点作直线，若直线与两坐标轴围成的三角形面积为4，则满足条件的直线的条数是　　‎ A．5 B．4 C．3 D．2‎ 二．填空题（共12小题）‎ ‎11．（2020•宿迁）已知一次函数的图象经过，，，两点，则　　（填“”“ ”或“” ．‎ ‎12．（2020•常州）若一次函数的函数值随自变量增大而增大，则实数的取值范围是　　．‎ ‎13．（2020•南京）将一次函数的图象绕原点逆时针旋转，所得到的图象对应的函数表达式是　　．‎ ‎14．（2020•连云港）如图，在平面直角坐标系中，半径为2的与轴的正半轴交于点，点是上一动点，点为弦的中点，直线与轴、轴分别交于点、，则面积的最小值为　　．‎ ‎15．（2020•苏州）若一次函数的图象与轴交于点，则　　．‎ ‎16．（2019•无锡）如图，已知、，一次函数的图象为直线，点关于直线的对称点恰好落在的平分线上，则的值为　　．‎ ‎17．（2019•徐州）函数的图象与轴、轴分别交于、两点，点在轴上．若为等腰三角形，则满足条件的点共有　　个．‎ ‎18．（2019•盐城）如图，在平面直角坐标系中，一次函数的图象分别交、轴于点、，将直线绕点按顺时针方向旋转，交轴于点，则直线的函数表达式是　　．‎ ‎19．（2019•无锡）已知一次函数的图象如图所示，则关于的不等式的解集为　　．‎ ‎20．（2018•淮安）如图，在平面直角坐标系中，直线为正比例函数的图象，点的坐标为，过点作轴的垂线交直线于点，以为边作正方形；过点作直线的垂线，垂足为，交轴于点，以为边作正方形；过点作轴的垂线，垂足为，交直线于点，以为边作正方形，，按此规律操作下所得到的正方形的面积是　　．‎ ‎21．（2018•连云港）如图，一次函数的图象与轴、轴分别相交于、两点，经过，两点，已知，则的值为　　．‎ ‎22．（2018•扬州）如图，在等腰，，点的坐标为，若直线把 分成面积相等的两部分，则的值为　　．‎ 三．解答题（共14小题）‎ ‎23．（2020•南通）如图，直线与过点的直线交于点，与轴交于点．‎ ‎（1）求直线的解析式；‎ ‎（2）点在直线上，轴，交直线于点，若，求点的坐标．‎ ‎24．（2020•淮安）甲、乙两地的路程为290千米，一辆汽车早上从甲地出发，匀速向乙地行驶，途中休息一段时间后．按原速继续前进，当离甲地路程为240千米时接到通知，要求中午准时到达乙地．设汽车出发小时后离甲地的路程为千米，图中折线表示接到通知前与之间的函数关系．‎ ‎（1）根据图象可知，休息前汽车行驶的速度为　　千米小时；‎ ‎（2）求线段所表示的与之间的函数表达式；‎ ‎（3）接到通知后，汽车仍按原速行驶能否准时到达？请说明理由．‎ ‎25．（2020•苏州）某商店代理销售一种水果，六月份的销售利润（元与销售量之间函数关系的图象如图中折线所示．请你根据图象及这种水果的相关销售记录提供的信息，解答下列问题：‎ ‎（1）截止到6月9日，该商店销售这种水果一共获利多少元？‎ ‎（2）求图象中线段所在直线对应的函数表达式．‎ 日期 销售记录 ‎6月1日 库存，成本价8元，售价10元（除了促销降价，其他时间售价保持不变）．‎ ‎6月9‎ 从6月1日至今，一共售出．‎ 日 ‎6月10、11日 这两天以成本价促销，之后售价恢复到10元．‎ ‎6月12日 补充进货，成本价8.5元．‎ ‎6月30日 水果全部售完，一共获利1200元．‎ ‎26．（2019•无锡）某校计划采购凳子，商场有、两种型号的凳子出售，并规定：对于型凳子，采购数量若超过250张，则超出部分可在原价基础上每张优惠元；型凳子的售价为40元张．学校经测算，若购买300张型凳子需要花费14250元；若购买500张型凳子需要花费21250元．‎ ‎（1）求的值；‎ ‎（2）学校要采购、两种型号凳子共900张，且购买型凳子不少于150张且不超过型凳子数量的2倍，请通过计算帮学校决策如何分配购买数量可以使得总采购费用最少？最少是多少元？‎ ‎27．（2019•徐州）如图①，将南北向的中山路与东西向的北京路看成两条直线，十字路口记作点．甲从中山路上点出发，骑车向北匀速直行；与此同时，乙从点出发，沿北京路步行向东匀速直行．设出发时，甲、乙两人与点的距离分别为、．已知、与之间的函数关系如图②所示．‎ ‎（1）求甲、乙两人的速度；‎ ‎（2）当取何值时，甲、乙两人之间的距离最短？‎ ‎28．（2019•镇江）学校数学兴趣小组利用机器人开展数学活动．‎ 在相距150个单位长度的直线跑道上，机器人甲从端点出发，匀速往返于端点、之间，机器人乙同时从端点出发，以大于甲的速度匀速往返于端点、之间．他们到达端点后立即转身折返，用时忽略不计．‎ 兴趣小组成员探究这两个机器人迎面相遇的情况，这里的”迎面相遇“包括面对面相遇、在端点处相遇这两种．‎ ‎【观察】‎ ‎①观察图1，若这两个机器人第一次迎面相遇时，相遇地点与点之间的距离为30个单位长度，则他们第二次迎面相遇时，相遇地点与点之间的距离为　　个单位长度；‎ ‎②若这两个机器人第一次迎面相遇时，相遇地点与点之间的距离为40个单位长度，则他们第二次迎面相 遇时，相遇地点与点之间的距离为　　个单位长度；‎ ‎【发现】‎ 设这两个机器人第一次迎面相遇时，相遇地点与点之间的距离为个单位长度，他们第二次迎面相遇时，相遇地点与点之间的距离为个单位长度．兴趣小组成员发现了与的函数关系，并画出了部分函数图象（线段，不包括点，如图2所示）．‎ ‎①　　；‎ ‎②分别求出各部分图象对应的函数表达式，并在图2中补全函数图象；‎ ‎【拓展】‎ 设这两个机器人第一次迎面相遇时，相遇地点与点之间的距离为个单位长度，他们第三次迎面相遇时，相遇地点与点之间的距离为个单位长度．‎ 若这两个机器人第三次迎面相遇时，相遇地点与点之间的距离不超过60个单位长度，则他们第一次迎面相遇时，相遇地点与点之间的距离的取值范围是　　．（直接写出结果）‎ ‎29．（2019•淮安）快车从甲地驶向乙地，慢车从乙地驶向甲地，两车同时出发并且在同一条公路上匀速行驶，途中快车休息1.5小时，慢车没有休息．设慢车行驶的时间为小时，快车行驶的路程为千米，慢车行驶的路程为千米．如图中折线表示与之间的函数关系，线段表示与之间的函数关系．‎ 请解答下列问题：‎ ‎（1）求快车和慢车的速度；‎ ‎（2）求图中线段所表示的与之间的函数表达式；‎ ‎（3）线段与线段相交于点，直接写出点的坐标，并解释点的实际意义．‎ ‎30．（2019•无锡）“低碳生活，绿色出行”是一种环保，健康的生活方式，小丽从甲地出发沿一条笔直的公路骑行前往乙地，她与乙地之间的距离与出发时间之间的函数关系式如图1中线段所示．在小丽出发的同时，小明从乙地沿同一条公路骑车匀速前往甲地，两人之间的距离与出发时间之间的函数关系式如图2中折线段所示．‎ ‎（1）小丽和小明骑车的速度各是多少？‎ ‎（2）求点的坐标，并解释点的实际意义．‎ ‎31．（2019•泰州）小李经营一家水果店，某日到水果批发市场批发一种水果．经了解，一次性批发这种水果不得少于，超过时，所有这种水果的批发单价均为3元．图中折线表示批发单价（元与质量的函数关系．‎ ‎（1）求图中线段所在直线的函数表达式；‎ ‎（2）小李用800元一次可以批发这种水果的质量是多少？‎ ‎32．（2019•无锡）一次函数的图象与轴的负半轴相交于点，与轴的正半轴相交于点，且．的外接圆的圆心的横坐标为．‎ ‎（1）求一次函数的解析式；‎ ‎（2）求图中阴影部分的面积．‎ ‎33．（2019•南京）已知一次函数为常数，和．‎ ‎（1）当时，若，求的取值范围．‎ ‎（2）当时，．结合图象，直接写出的取值范围．‎ ‎34．（2019•连云港）某工厂计划生产甲、乙两种产品共2500吨，每生产1吨甲产品可获得利润0.3万元，每生产1吨乙产品可获得利润0.4万元．设该工厂生产了甲产品（吨，生产甲、乙两种产品获得的总利润为（万元）．‎ ‎（1）求与之间的函数表达式；‎ ‎（2）若每生产1吨甲产品需要原料0.25吨，每生产1吨乙产品需要原料0.5吨．受市场影响，该厂能获得的原料至多为1000吨，其它原料充足．求出该工厂生产甲、乙两种产品各为多少吨时，能获得最大利润．‎ ‎35．（2018•南通）【定义】如图1，，为直线同侧的两点，过点作直线1的对称点，连接交 直线于点，连接，则称点为点，关于直线的“等角点”．‎ ‎【运用】如图2，在平面直角坐标系中，已知，两点．‎ ‎（1），，三点中，点　　是点，关于直线的等角点；‎ ‎（2）若直线垂直于轴，点是点，关于直线的等角点，其中，，求证：；‎ ‎（3）若点是点，关于直线的等角点，且点位于直线的右下方，当时，求的取值范围（直接写出结果）．‎ ‎36．（2018•镇江）如图，一次函数的图象与轴，轴分别交于，两点，过点作直线与垂直，点在直线位于轴上方的部分．‎ ‎（1）求一次函数的表达式；‎ ‎（2）若的面积为11，求点的坐标；‎ ‎（3）当时，点的坐标为　　．‎ ‎2018—2020年江苏省数学中考试题分类（8）——一次函数 一．选择题（共10小题）‎ ‎1．（2020•宿迁）如图，在平面直角坐标系中，是直线上的一个动点，将绕点顺时针旋转，得到点，连接，则的最小值为　　‎ A． B． C． D．‎ ‎【解答】解：作轴于点，轴于，‎ ‎，‎ ‎，‎ 在和△中，‎ ‎△，‎ ‎，，‎ 设，‎ ‎，，‎ ‎，‎ ‎，，‎ ‎，‎ 当时，有最小值为5，‎ 的最小值为，‎ 当时，有最小值为5，‎ 故选：．‎ ‎2．（2020•镇江）一次函数的函数值随的增大而增大，它的图象不经过的象限是　　‎ A．第一 B．第二 C．第三 D．第四 ‎【解答】解：一次函数的函数值随的增大而增大，‎ ‎，该函数过点，‎ 该函数的图象经过第一、二、三象限，不经过第四象限，‎ 故选：．‎ ‎3．（2020•连云港）快车从甲地驶往乙地，慢车从乙地驶往甲地，两车同时出发并且在同一条公路上匀速行驶．图中折线表示快、慢两车之间的路程与它们的行驶时间之间的函数关系．小欣同学结合图象得出如下结论：‎ ‎①快车途中停留了；‎ ‎②快车速度比慢车速度多；‎ ‎③图中；‎ ‎④快车先到达目的地．‎ 其中正确的是　　‎ A．①③ B．②③ C．②④ D．①④‎ ‎【解答】解：根据题意可知，两车的速度和为：，‎ 相遇后慢车停留了，快车停留了，此时两车距离为，故①结论错误；‎ 慢车的速度为：，则快车的速度为，‎ 所以快车速度比慢车速度多；故②结论正确；‎ ‎，‎ 所以图中，故③结论正确；‎ 快车到达终点的时间为小时，‎ 慢车到达终点的时间为小时，‎ 因为，‎ 所以慢车先到达目的地，故④结论错误．‎ 所以正确的是②③．‎ 故选：．‎ ‎4．（2020•泰州）点在函数的图象上，则代数式的值等于　　‎ A．5 B．3 C． D．‎ ‎【解答】解：点在函数的图象上，‎ ‎，‎ 则．‎ 故选：．‎ ‎5．（2019•苏州）若一次函数，为常数，且的图象经过点，，则不等式的解集为　　‎ A． B． C． D．‎ ‎【解答】解：如图所示：不等式的解为：．‎ 故选：．‎ ‎6．（2019•扬州）若点在一次函数的图象上，则点一定不在　　‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎【解答】解：，，‎ 一次函数的图象经过第一、二、四象限，即不经过第三象限．‎ 点在一次函数的图象上，‎ 点一定不在第三象限．‎ 故选：．‎ ‎7．（2018•徐州）若函数的图象如图所示，则关于的不等式的解集为　　‎ A． B． C． D．‎ ‎【解答】解：一次函数经过点，且随的增大而减小，‎ ‎，且，‎ 则，‎ ‎，‎ ‎，‎ 则，即，‎ 故选：．‎ ‎8．（2018•常州）一个正比例函数的图象经过，则它的表达式为　　‎ A． B． C． D．‎ ‎【解答】解：设该正比例函数的解析式为，‎ 正比例函数的图象经过点，‎ ‎，解得，‎ 这个正比例函数的表达式是．‎ 故选：．‎ ‎9．（2018•泰州）如图，平面直角坐标系中，点的坐标为，轴，垂足为，点从原点出发向轴正方向运动，同时，点从点出发向点运动，当点到达点时，点、同时停止运动，若点与点的速度之比为，则下列说法正确的是　　‎ A．线段始终经过点 ‎ B．线段始终经过点 ‎ C．线段始终经过点 ‎ D．线段不可能始终经过某一定点 ‎【解答】解：当时，点的坐标为，点的坐标为．‎ 设直线的解析式为，‎ 将、代入，‎ ‎，解得：，‎ 直线的解析式为．‎ 两边乘得到：，‎ ‎，‎ 当时，，‎ 直线始终经过，‎ 故选：．‎ ‎10．（2018•宿迁）在平面直角坐标系中，过点作直线，若直线与两坐标轴围成的三角形面积为4，则满足条件的直线的条数是　　‎ A．5 B．4 C．3 D．2‎ ‎【解答】解：设过点的直线的函数解析式为，‎ ‎，得，‎ ‎，‎ 当时，，当时，，‎ 令，‎ 化简，得 ‎，‎ 当时，，‎ 解得，，‎ 当时，，‎ 解得，，，‎ 故满足条件的直线的条数是3条，‎ 故选：．‎ 二．填空题（共12小题）‎ ‎11．（2020•宿迁）已知一次函数的图象经过，，，两点，则　　（填“”“ ”或“” ．‎ ‎【解答】解：（解法一），‎ 随的增大而增大．‎ 又，‎ ‎．‎ 故答案为：．‎ ‎（解法二）当时，，‎ 解得：；‎ 当时，，‎ 解得：．‎ 又，‎ ‎．‎ 故答案为：．‎ ‎12．（2020•常州）若一次函数的函数值随自变量增大而增大，则实数的取值范围是　　．‎ ‎【解答】解：一次函数，函数值随的值增大而增大，‎ ‎．‎ 故答案为：．‎ ‎13．（2020•南京）将一次函数的图象绕原点逆时针旋转，所得到的图象对应的函数表达式是　　．‎ ‎【解答】解：在一次函数中，令，则，令，则，‎ 直线经过点，‎ 将一次函数的图象绕原点逆时针旋转，则点的对应点为，的对应点是 设对应的函数解析式为：，‎ 将点、代入得，解得，‎ 旋转后对应的函数解析式为：，‎ 故答案为．‎ ‎14．（2020•连云港）如图，在平面直角坐标系中，半径为2的与轴的正半轴交于点，点是上一动点，点为弦的中点，直线与轴、轴分别交于点、，则面积的最小值为　2　．‎ ‎【解答】解：如图，连接，取的中点，连接，过点作于．‎ ‎，，‎ ‎，‎ 点的运动轨迹是以为圆心，1为半径的，设交于．‎ 直线与轴、轴分别交于点、，‎ ‎，，‎ ‎，，‎ ‎，‎ ‎，，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ 当点与重合时，△的面积最小，△的面积最小值，‎ 故答案为2．‎ ‎15．（2020•苏州）若一次函数的图象与轴交于点，则　2　．‎ ‎【解答】解：一次函数的图象与轴交于点，‎ ‎，‎ 解得，‎ 故答案为2．‎ ‎16．（2019•无锡）如图，已知、，一次函数的图象为直线，点关于直线的对称点恰好落在的平分线上，则的值为　　．‎ ‎【解答】解：延长交于点，交于点，过点作轴交于，过点作轴于点； ‎ ‎、，‎ 直线的解析式为，‎ 直线的解析式为，‎ ‎，‎ ‎，‎ ‎，‎ ‎，，‎ 由等积法可求，，‎ ‎，‎ ‎，‎ 是的角平分线，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ 在△中，，‎ ‎、是△的中位线，‎ ‎，，‎ 点在直线上，‎ ‎，‎ ‎，‎ 故答案为．‎ ‎17．（2019•徐州）函数的图象与轴、轴分别交于、两点，点在轴上．若为等腰三角形，则满足条件的点共有　4　个．‎ ‎【解答】解以点为圆心，为半径作圆，与轴交点即为；‎ 以点为圆心，为半径作圆，与轴交点即为；‎ 作的中垂线与轴的交点即为；‎ 故答案为4；‎ ‎18．（2019•盐城）如图，在平面直角坐标系中，一次函数的图象分别交、轴于点、，将直线绕点按顺时针方向旋转，交轴于点，则直线的函数表达式是　　．‎ ‎【解答】解：一次函数的图象分别交、轴于点、，‎ 令，得，令，则，‎ ‎，，，‎ ‎，，‎ 过作交于，过作轴于，‎ ‎，‎ 是等腰直角三角形，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，，‎ ‎，，‎ 设直线的函数表达式为：，‎ ‎，‎ ‎，‎ 直线的函数表达式为：，‎ 故答案为：．‎ ‎19．（2019•无锡）已知一次函数的图象如图所示，则关于的不等式的解集为　　．‎ ‎【解答】解：图象过，则，‎ 则，‎ 故，‎ ‎，‎ ‎，‎ 解得：．‎ 故答案为：．‎ ‎20．（2018•淮安）如图，在平面直角坐标系中，直线为正比例函数的图象，点的坐标为，过点作轴的垂线交直线于点，以为边作正方形；过点作直线的垂线，垂足为，交轴于点，以为边作正方形；过点作轴的垂线，垂足为，交直线于点，以为边作正方形，，按此规律操作下所得到的正方形的面积是　　．‎ ‎【解答】解：直线为正比例函数的图象，‎ ‎，‎ ‎，‎ 正方形的面积，‎ 由勾股定理得，，，‎ ‎，‎ 正方形的面积，‎ 同理，，‎ 正方形的面积，‎ 由规律可知，正方形的面积，‎ 故答案为：．‎ ‎21．（2018•连云港）如图，一次函数的图象与轴、轴分别相交于、两点，经过，两点，已知，则的值为　　．‎ ‎【解答】解：由图形可知：是等腰直角三角形，‎ ‎，‎ 点坐标是，，点坐标是 一次函数的图象与轴、轴分别相交于、两点 将，两点坐标代入，得，‎ 故答案为：‎ ‎22．（2018•扬州）如图，在等腰，，点的坐标为，若直线把分成面积相等的两部分，则的值为　　．‎ ‎【解答】解：，‎ 函数一定过点，‎ 当时，，‎ 点的坐标为，‎ 由题意可得，直线的解析式为，‎ ‎，得，‎ 直线把分成面积相等的两部分，‎ ‎，‎ 解得，，（舍去），‎ 故答案为：．‎ 三．解答题（共14小题）‎ ‎23．（2020•南通）如图，直线与过点的直线交于点，与轴交于点．‎ ‎（1）求直线的解析式；‎ ‎（2）点在直线上，轴，交直线于点，若，求点的坐标．‎ ‎【解答】解：（1）在中，令，得，‎ ‎，‎ 把代入得，‎ ‎，‎ 设直线的解析式为，‎ ‎，解得，‎ 直线的解析式为；‎ ‎（2），‎ 设，由轴，得，‎ ‎，‎ 解得或，‎ 或．‎ ‎24．（2020•淮安）甲、乙两地的路程为290千米，一辆汽车早上从甲地出发，匀速向乙地行驶，途中休息一段时间后．按原速继续前进，当离甲地路程为240千米时接到通知，要求中午准时到达乙地．设汽车出发小时后离甲地的路程为千米，图中折线表示接到通知前与之间的函数关系．‎ ‎（1）根据图象可知，休息前汽车行驶的速度为　80　千米小时；‎ ‎（2）求线段所表示的与之间的函数表达式；‎ ‎（3）接到通知后，汽车仍按原速行驶能否准时到达？请说明理由．‎ ‎【解答】解：（1）由图象可知，休息前汽车行驶的速度为80千米小时；‎ 故答案为：80；‎ ‎（2）休息后按原速继续前进行驶的时间为：（小时），‎ 点的坐标为，‎ 设线段所表示的与之间的函数表达式为，则：‎ ‎，解得，‎ 线段所表示的与之间的函数表达式为：；‎ ‎（3）接到通知后，汽车仍按原速行驶，则全程所需时间为：（小时），‎ ‎（小时），‎ ‎，‎ 所以接到通知后，汽车仍按原速行驶不能准时到达．‎ ‎25．（2020•苏州）某商店代理销售一种水果，六月份的销售利润（元与销售量之间函数关系的图象如图中折线所示．请你根据图象及这种水果的相关销售记录提供的信息，解答下列问题：‎ ‎（1）截止到6月9日，该商店销售这种水果一共获利多少元？‎ ‎（2）求图象中线段所在直线对应的函数表达式．‎ 日期 销售记录 ‎6月1日 库存，成本价8元，售价10元（除了促销降价，其他时间售价保持不变）．‎ ‎6月9日 从6月1日至今，一共售出．‎ ‎6月10、11日 这两天以成本价促销，之后售价恢复到10元．‎ ‎6月12日 补充进货，成本价8.5元．‎ ‎6月30日 水果全部售完，一共获利1200元．‎ ‎【解答】解：（1）（元 答：截止到6月9日，该商店销售这种水果一共获利400元；‎ ‎（2）设点坐标为，根据题意得：‎ ‎，‎ 解这个方程，得，‎ 点坐标为，‎ 设线段所在直线对应的函数表达式为，则：‎ ‎，解得，‎ 线段所在直线对应的函数表达式为．‎ ‎26．（2019•无锡）某校计划采购凳子，商场有、两种型号的凳子出售，并规定：对于型凳子，采购数量若超过250张，则超出部分可在原价基础上每张优惠元；型凳子的售价为40元张．学校经测算，若购买300张型凳子需要花费14250元；若购买500张型凳子需要花费21250元．‎ ‎（1）求的值；‎ ‎（2）学校要采购、两种型号凳子共900张，且购买型凳子不少于150张且不超过型凳子数量的2倍，请通过计算帮学校决策如何分配购买数量可以使得总采购费用最少？最少是多少元？‎ ‎【解答】解：（1）设型凳子的售价为元张，根据题意得 ‎，‎ 解得，‎ 答：的值为15．‎ ‎（2）设购买型凳子张，则购买型凳子张，‎ 根据题意得，‎ 解得，‎ 设总采购费用为元，根据题意得 当时，；‎ 当时，，‎ ‎，‎ 当时，，随的增大而增大，时，的最小值为37500；‎ 当时，，随的增大而减小，时，的最小值为36750．‎ ‎，‎ 购买型凳子600张，购买型凳子300张时总采购费用最少，最少是36750元．‎ ‎27．（2019•徐州）如图①，将南北向的中山路与东西向的北京路看成两条直线，十字路口记作点．甲从中山路上点出发，骑车向北匀速直行；与此同时，乙从点出发，沿北京路步行向东匀速直行．设出发时，甲、乙两人与点的距离分别为、．已知、与之间的函数关系如图②所示．‎ ‎（1）求甲、乙两人的速度；‎ ‎（2）当取何值时，甲、乙两人之间的距离最短？‎ ‎【解答】解：（1）设甲、乙两人的速度分别为，，则：‎ 由图②知：或7.5时，，，解得：‎ ‎，令，则 ‎ ‎ 答：甲的速度为，乙的速度为．‎ ‎（2）设甲、乙之间距离为，‎ 则 ‎，‎ 当时，的最小值为144000，即的最小值为；‎ 答：当时，甲、乙两人之间的距离最短．‎ ‎28．（2019•镇江）学校数学兴趣小组利用机器人开展数学活动．‎ 在相距150个单位长度的直线跑道上，机器人甲从端点出发，匀速往返于端点、之间，机器人乙同时从端点出发，以大于甲的速度匀速往返于端点、之间．他们到达端点后立即转身折返，用时忽略不计．‎ 兴趣小组成员探究这两个机器人迎面相遇的情况，这里的”迎面相遇“包括面对面相遇、在端点处相遇这两种．‎ ‎【观察】‎ ‎①观察图1，若这两个机器人第一次迎面相遇时，相遇地点与点之间的距离为30个单位长度，则他们第二次迎面相遇时，相遇地点与点之间的距离为　90　个单位长度；‎ ‎②若这两个机器人第一次迎面相遇时，相遇地点与点之间的距离为40个单位长度，则他们第二次迎面相遇时，相遇地点与点之间的距离为　　个单位长度；‎ ‎【发现】‎ 设这两个机器人第一次迎面相遇时，相遇地点与点之间的距离为个单位长度，他们第二次迎面相遇时，相遇地点与点之间的距离为个单位长度．兴趣小组成员发现了与的函数关系，并画出了部分函数图象（线段，不包括点，如图2所示）．‎ ‎①　　；‎ ‎②分别求出各部分图象对应的函数表达式，并在图2中补全函数图象；‎ ‎【拓展】‎ 设这两个机器人第一次迎面相遇时，相遇地点与点之间的距离为个单位长度，他们第三次迎面相遇时，相遇地点与点之间的距离为个单位长度．‎ 若这两个机器人第三次迎面相遇时，相遇地点与点之间的距离不超过60个单位长度，则他们第一次迎面相遇时，相遇地点与点之间的距离的取值范围是　　．（直接写出结果）‎ ‎【解答】解：【观察】①相遇地点与点之间的距离为30个单位长度，‎ 相遇地点与点之间的距离为个单位长度，‎ 设机器人甲的速度为，‎ 机器人乙的速度为，‎ 机器人甲从相遇点到点所用的时间为，‎ 机器人乙从相遇地点到点再返回到点所用时间为，而，‎ 设机器人甲与机器人乙第二次迎面相遇时，‎ 机器人乙从第一次相遇地点到点，返回到点，再返回向时和机器人甲第二次迎面相遇，‎ 设此时相遇点距点为个单位，‎ 根据题意得，，‎ ‎，‎ 故答案为：90；‎ ‎②相遇地点与点之间的距离为40个单位长度，‎ 相遇地点与点之间的距离为个单位长度，‎ 设机器人甲的速度为，‎ 机器人乙的速度为，‎ 机器人乙从相遇点到点再到点所用的时间为，‎ 机器人甲从相遇点到点所用时间为，而，‎ 设机器人甲与机器人乙第二次迎面相遇时，机器人从第一次相遇点到点，再到点，返回时和机器人乙第二次迎面相遇，‎ 设此时相遇点距点为个单位，‎ 根据题意得，，‎ ‎，‎ 故答案为：120；‎ ‎【发现】①当点第二次相遇地点刚好在点时，‎ 设机器人甲的速度为，则机器人乙的速度为，‎ 根据题意知，，‎ ‎，‎ 即：，‎ 故答案为：50；‎ ‎②当时，点在线段上，‎ 线段的表达式为，‎ 当时，即当，此时，第二次相遇地点是机器人甲在到点返回向点时，‎ 设机器人甲的速度为，则机器人乙的速度为，‎ 根据题意知，，‎ ‎，‎ 即：，‎ 补全图形如图2所示，‎ ‎【拓展】①如图，‎ 由题意知，，‎ ‎，‎ ‎，‎ ‎；‎ ‎②如图，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎③如图，‎ 由题意得，，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ 综上所述，相遇地点与点之间的距离的取值范围是或，‎ 故答案为或．‎ ‎29．（2019•淮安）快车从甲地驶向乙地，慢车从乙地驶向甲地，两车同时出发并且在同一条公路上匀速行驶，途中快车休息1.5小时，慢车没有休息．设慢车行驶的时间为小时，快车行驶的路程为千米，慢车行驶的路程为千米．如图中折线表示与之间的函数关系，线段表示与之间的函数关系．‎ 请解答下列问题：‎ ‎（1）求快车和慢车的速度；‎ ‎（2）求图中线段所表示的与之间的函数表达式；‎ ‎（3）线段与线段相交于点，直接写出点的坐标，并解释点的实际意义．‎ ‎【解答】解：（1）快车的速度为：千米小时，‎ 慢车的速度为：千米小时，‎ 答：快车的速度为90千米小时，慢车的速度为60千米小时；‎ ‎（2）由题意可得，‎ 点的横坐标为：，‎ 则点的坐标为，‎ 快车从点到点用的时间为：（小时），‎ 则点的坐标为，‎ 设线段所表示的与之间的函数表达式是，‎ ‎，得，‎ 即线段所表示的与之间的函数表达式是；‎ ‎（3）设点的横坐标为，‎ 则，‎ 解得，，‎ 则，‎ 即点的坐标为，点代表的实际意义是在4.5小时时，甲车与乙车行驶的路程相等．‎ ‎30．（2019•无锡）“低碳生活，绿色出行”是一种环保，健康的生活方式，小丽从甲地出发沿一条笔直的公路骑行前往乙地，她与乙地之间的距离与出发时间之间的函数关系式如图1中线段所示．在小丽出发的同时，小明从乙地沿同一条公路骑车匀速前往甲地，两人之间的距离与出发时间之间的函数关系式如图2中折线段所示．‎ ‎（1）小丽和小明骑车的速度各是多少？‎ ‎（2）求点的坐标，并解释点的实际意义．‎ ‎【解答】解：（1）由题意可得：小丽速度 设小明速度为 由题意得：‎ 答：小明的速度为，小丽的速度为．‎ ‎（2）由图象可得：点表示小明到了甲地，此时小丽没到，‎ 点的横坐标，‎ 点的纵坐标 点，‎ ‎31．（2019•泰州）小李经营一家水果店，某日到水果批发市场批发一种水果．经了解，一次性批发这种水果不得少于，超过时，所有这种水果的批发单价均为3元．图中折线表示批发单价（元与质量的函数关系．‎ ‎（1）求图中线段所在直线的函数表达式；‎ ‎（2）小李用800元一次可以批发这种水果的质量是多少？‎ ‎【解答】解：（1）设线段所在直线的函数表达式为，根据题意得 ‎，解得，‎ 线段所在直线的函数表达式为；‎ ‎（2）设小李共批发水果千克，则单价为，‎ 根据题意得：，‎ 解得或，‎ 经检验，，（不合题意，舍去）都是原方程的根．‎ 答：小李用800元一次可以批发这种水果的质量是200千克．‎ ‎32．（2019•无锡）一次函数的图象与轴的负半轴相交于点，与轴的正半轴相交于点，且．的外接圆的圆心的横坐标为．‎ ‎（1）求一次函数的解析式；‎ ‎（2）求图中阴影部分的面积．‎ ‎【解答】解：（1）过点作于点，‎ 由垂径定理得：点为的中点，‎ ‎，‎ ‎，，即，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ 即，‎ 设，将、代入得：，‎ ‎（2），，‎ ‎，则，‎ ‎，‎ 阴影部分面积为．‎ ‎33．（2019•南京）已知一次函数为常数，和．‎ ‎（1）当时，若，求的取值范围．‎ ‎（2）当时，．结合图象，直接写出的取值范围．‎ ‎【解答】解：（1）时，，‎ 根据题意得，‎ 解得；‎ ‎（2）当时，，把代入得，解得，‎ 当时，；‎ 当时，．‎ 所以的范围为且．‎ ‎34．（2019•连云港）某工厂计划生产甲、乙两种产品共2500吨，每生产1吨甲产品可获得利润0.3万元，每生产1吨乙产品可获得利润0.4万元．设该工厂生产了甲产品（吨，生产甲、乙两种产品获得的总利润为（万元）．‎ ‎（1）求与之间的函数表达式；‎ ‎（2）若每生产1吨甲产品需要原料0.25吨，每生产1吨乙产品需要原料0.5吨．受市场影响，该厂能获得的原料至多为1000吨，其它原料充足．求出该工厂生产甲、乙两种产品各为多少吨时，能获得最大利润．‎ ‎【解答】解：（1）‎ ‎ 因此与之间的函数表达式为：．‎ ‎ （2）由题意得：‎ ‎ 又 随的增大而减少 当时，最大，此时，‎ ‎ 因此，生产甲产品1000吨，乙产品1500吨时，利润最大．‎ ‎35．（2018•南通）【定义】如图1，，为直线同侧的两点，过点作直线1的对称点，连接交直线于点，连接，则称点为点，关于直线的“等角点”．‎ ‎【运用】如图2，在平面直角坐标系中，已知，两点．‎ ‎（1），，三点中，点　　是点，关于直线的等角点；‎ ‎（2）若直线垂直于轴，点是点，关于直线的等角点，其中，，求证：；‎ ‎（3）若点是点，关于直线的等角点，且点位于直线的右下方，当时，求的取值范围（直接写出结果）．‎ ‎【解答】解：（1）点关于直线的对称点为，‎ 直线解析式为：，‎ 当时，．‎ 故答案为：；‎ ‎（2）如图，过点作直线的对称点，连，交直线于点．作于点．‎ 点和关于直线对称，‎ ‎，‎ ‎，‎ ‎，‎ 又，‎ ‎，‎ ‎，即，‎ ‎，即．‎ ‎，，‎ ‎，‎ 在中，；‎ ‎（3）点位于直线的右下方，时，点在以为弦，所对圆周角为，且圆心在下方，如图．‎ 若直线与圆相交，设圆与直线的另一个交点为．‎ 由对称性可知：，‎ 又，‎ ‎，‎ ‎，，‎ ‎，‎ 是等边三角形．‎ 线段为定线段，‎ 点为定点．‎ 若直线与圆相切，易得、重合，‎ 直线过定点．‎ 连，过点、分别作轴，轴，垂足分别为、．‎ ‎，，‎ ‎．‎ 是等边三角形，‎ ‎，，‎ ‎，‎ 又，，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，，‎ 点坐标为．‎ 设直线解析式为，‎ 将、坐标代入得，‎ 解得，‎ 直线的解析式为：．‎ 设直线的解析式为：，‎ 将、两点代入得，‎ 解得，‎ 直线的解析式为：．‎ 若点与点重合，则直线与直线重合，此时，；‎ 若点与点重合，则直线与直线重合，此时，．‎ 又，且点位于右下方，‎ 或．‎ ‎36．（2018•镇江）如图，一次函数的图象与轴，轴分别交于，两点，过点作直线与垂直，点在直线位于轴上方的部分．‎ ‎（1）求一次函数的表达式；‎ ‎（2）若的面积为11，求点的坐标；‎ ‎（3）当时，点的坐标为　　．‎ ‎【解答】解：（1）一次函数的图象与轴，轴分别交于，两点，‎ ‎，‎ ‎，‎ 一次函数的表达式为；‎ ‎（2）如图，记直线与轴的交点为，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，，‎ ‎，，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ 直线的解析式为，‎ 设，‎ ‎，，‎ ‎，‎ ‎，‎ ‎；‎ ‎（3）如图，过点作轴于，连接，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，，‎ ‎，‎ ‎．‎ 故答案为．‎