- 1.09 MB
- 2021-11-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
考点跟踪突破
21
特殊三角形
一、选择题
(
每小题
6
分
,
共
30
分
)
1
.
(
2014
·
黄石
)
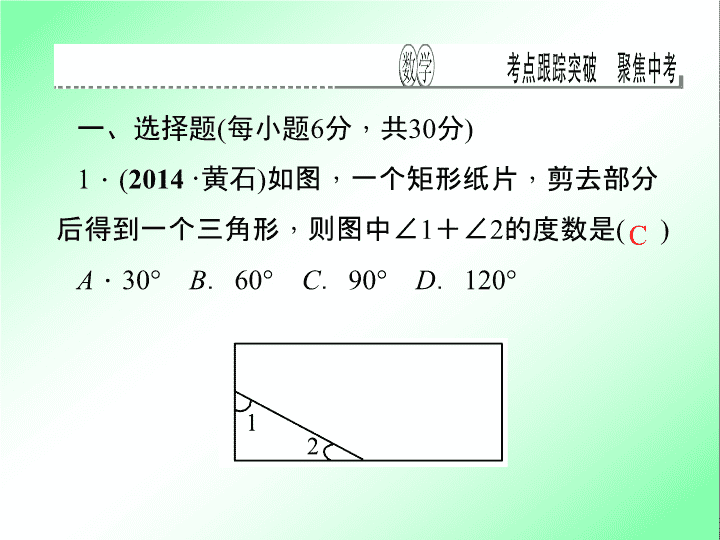
如图
,
一个矩形纸片
,
剪去部分后得到一个三角形
,
则图中
∠
1
+
∠
2
的度数是
(
)
A
.
30°
B
.
60°
C
.
90°
D
.
120°
C
2
.
(
2013
·
攀枝花
)
如图
,
在
△
ABC
中
,
∠
CAB
=
75°
,
在同一平面内
,
将
△
ABC
绕点
A
旋转到
△
AB
′
C
′
的位置
,
使得
CC
′
∥
AB
,
则
∠
BAB
′
=
( )
A
.
30° B
.
35° C
.
40° D
.
50°
A
3
.
(
2014·
广东
)
一个等腰三角形的两边长分别是
3
和
7
,
则它的周长为
(
)
A
.
17
B
.
15
C
.
13
D
.
13
或
17
4
.
(
2014·
滨州
)
下列四组线段中
,
可以构成直角三角形的
是
(
)
A
.
4
,
5
,
6
B
.
1.5
,
2
,
2.5
C
.
2
,
3
,
4
D
.
1
,
2
,
3
A
B
5
.
如图
,
在
△
ABC
中
,
∠
C
=
90
°
,
AC
=
BC
=
4
,
点
D
是
AB
的中
点
,
点
E
,
F
分别在
AC
,
BC
边上运动
(
点
E
不与点
A
,
C
重合
)
,
且
保持
AE
=
CF
,
连接
DE
,
DF
,
EF
.
在此运动变化的过程中
,
有下列
结论:
①△
DFE
是等腰直角三角形
;
②
四边形
CEDF
不可能为正方形;
③
四边形
CEDF
的面积随点
E
位置的改变而发生变化;
④
点
C
到线段
EF
的最大距离为
2
.
其中正确的有
(
)
A
.
1
个
B
.
2
个
C
.
3
个
D
.
4
个
B
二、填空题
(
每小题
6
分
,
共
30
分
)
6
.
(
2014
·
临夏
)
等腰
△
ABC
中
,
AB
=
AC
=
10
cm
,
BC
=
12
cm
,
则
BC
边上的高是
____
cm
.
7
.
(
2014
·
呼和浩特
)
等腰三角形一腰上的高与另一腰的夹角为
36°
,
则该等腰三角形的底角的度数
为
.
63°
或
27°
8
8
.
(
2013
·
黄冈
)
已知
△
ABC
为等边三角形
,
BD
为中线
,
延长
BC
至点
E
,
使
CE
=
CD
=
1
,
连接
DE
,
则
DE
=
____
.
9
.
(
2014·
凉山
)
已知一个直角三角形的两边的长分别是
3
和
4
,
则第三边长为
.
10
.
(
2013·
张家界
)
如图
,
OP
=
1
,
过点
P
作
PP
1
⊥
OP
,
得
OP
1
=
2
;再过点
P
1
作
P
1
P
2
⊥
OP
1
且
P
1
P
2
=
1
,
得
OP
2
=
3
;
又过点
P
2
作
P
2
P
3
⊥
OP
2
且
P
2
P
3
=
1
,
得
OP
3
=
2
……
依此法
继续作下去
,
得
OP
2012
=
.
11
.
(10
分
)
(
2014
·
襄阳
)
如图
,
在
△
ABC
中
,
点
D
,
E
分别在边
AC
,
AB
上
,
BD
与
CE
交于点
O
,
给出下列三个条件:
①∠
EBO
=
∠
DCO
;
②
BE
=
CD
;
③
OB
=
OC.
(1)
上述三个条件中
,
由哪两个条件可以判定
△
ABC
是等腰三角形?
(
用序号写出所有成立的情形
)
(2)
请选择
(1)
中的一种情形
,
写出证明过程.
解:
(1)
①②
;
①③
(2)
选
①③
证明如下
,
∵
OB
=
OC
,
∴∠
OBC
=
∠
OCB
,
∵∠
EBO
=
∠
DCO
,
又
∵∠
ABC
=
∠
EBO
+
∠
OBC
,
∠
ACB
=
∠
DCO
+
∠
OCB
,
∴∠
ABC
=
∠
ACB
,
∴△
ABC
是等腰三角形
12
.
(10
分
)
(
2014
·
温州
)
如图
,
在等边三角形
ABC
中
,
点
D
,
E
分别在边
BC
,
AC
上
,
DE
∥
AB
,
过点
E
作
EF
⊥
DE
,
交
BC
的延长线于点
F.
(1)
求
∠
F
的度数;
(2)
若
CD
=
2
,
求
DF
的长.
∵△
ABC
是等边三角形
,
∴∠
B
=
60°
,
∵
DE
∥
AB
,
∴∠
EDC
=
∠
B
=
60°
,
∵
EF
⊥
DE
,
∴∠
DEF
=
90°
,
∴∠
F
=
90°
-
∠
EDC
=
30°
∵∠
ACB
=
60°
,
∠
EDC
=
60°
,
∴△
EDC
是等边三角形.
∴
ED
=
DC
=
2
,
∵∠
DEF
=
90°
,
∠
F
=
30°
,
∴
DF
=
2DE
=
4
13
.
(10
分
)
(
2012
·
泰安
)
如图
,
在
△
ABC
中
,
∠
ABC
=
45°
,
CD
⊥
AB
,
BE
⊥
AC
,
垂足分别为点
D
,
E
,
点
F
为
BC
中点
,
BE
与
DF
,
DC
分别交于点
G
,
H
,
∠
ABE
=
∠
CBE.
(1)
线段
BH
与
AC
相等吗
,
若相等给予证明
,
若不相等请说明理由;
(2)
求证:
BG
2
-
GE
2
=
EA
2
.
(2)
连接
CG
,
∵
F
为
BC
的中点
,
DB
=
DC
,
∴
DF
垂直平分
BC
,
∴
BG
=
CG
,
∵∠
ABE
=
∠
CBE
,
BE
⊥
AC
,
在
Rt
△
ABE
和
Rt
△
CBE
中
,
∠
AEB
=
∠
CEB
,
BE
=
BE
,
∠
CBE
=
∠
ABE
,
∴△
ABE
≌△
CBE(
ASA
)
,
∴
EC
=
EA.
在
Rt
△
CGE
中
,
由勾股定理得
CG
2
-
GE
2
=
EC
2
,
∴
BG
2
-
GE
2
=
EA
2
14
.
(10
分
)
(
2013
·
常德
)
已知两个共一个顶点的等腰
Rt
△
ABC
,
Rt
△
CEF
,
∠
ABC
=
∠
CEF
=
90°
,
连接
AF
,
M
是
AF
的中点
,
连接
MB
,
ME.
(1)
如图
①
,
当
CB
与
CE
在同一直线上时
,
求证:
MB
∥
CF
;
(2)
如图
①
,
若
CB
=
a
,
CE
=
2a
,
求
BM
,
ME
的长;
(3)
如图
②
,
当
∠
BCE
=
45°
时
,
求证:
BM
=
ME.
解:
(
1
)
证法一:如图
①
,
延长
AB
交
CF
于点
D
,
则易知
△
ABC
与
△
BCD
均为等腰直角三
角形
,
∴
AB
=
BC
=
BD
,
∴
点
B
为线段
AD
的中点
,
又
∵
点
M
为线段
AF
的中点
,
∴
BM
为
△
ADF
的中位线
,
∴
BM
∥
CF
证法二:如图
②
,
延长
BM
交
EF
于点
D
,
∵∠
ABC
=
∠
CEF
=
90
°
,
∴
AB
⊥
CE
,
EF
⊥
CE
,
∴
AB
∥
EF
,
∴∠
BAM
=
∠
DFM
,
∵
M
是
AF
的中点
,
∴
AM
=
FM
,
∵
在
△
ABM
和
△
FDM
中
,
î
í
ì
∠
BAM
=
∠
DFM
,
AM
=
FM
,
∠
AMB
=
∠
FMD
,
∴△
ABM
≌△
FDM
(
ASA
)
,
∴
AB
=
DF
,
∵
BE
=
CE
-
BC
,
DE
=
EF
-
DF
,
∴
BE
=
DE
,
∴△
BDE
是等腰直角三角形
,
∴∠
EBM
=
45
°
,
∵
在等腰直角
△
CEF
中
,
∠
ECF
=
45
°
,
∴∠
EBM
=
∠
ECF
,
∴
MB
∥
CF
(
2
)
如图
③
所示
,
延长
AB
交
CF
于点
D
,
则易
知
△
BCD
与
△
ABC
为等腰直角三角形
,
∴
AB
=
BC
=
BD
=
a
,
AC
=
CD
=
2
a
,
∴
点
B
为
AD
中点
,
又
∵
点
M
为
AF
中点
,
∴
BM
=
1
2
DF.
分别延长
FE
与
CA
交于点
G
,
则易知
△
CEF
与
△
CEG
均为等腰直角三
角形
,
∴
CE
=
EF
=
GE
=
2a
,
CG
=
CF
=
2
2
a
,
∴
点
E
为
FG
中点
,
又点
M
为
AF
中点
,
∴
ME
=
1
2
AG.
∵
CG
=
CF
=
2
2
a
,
CA
=
CD
=
2
a
,
∴
AG
=
DF
=
2
a
,
∴
BM
=
ME
=
1
2
×
2
a
=
2
2
a
(
3
)
证法一:如图
④
,
延长
AB
交
CE
于点
D
,
连接
DF
,
则易知
△
ABC
与
△
BCD
均
为等腰直角三角形
,
∴
AB
=
BC
=
BD
,
AC
=
CD
,
∴
点
B
为
AD
中点
,
又点
M
为
AF
中点
,
∴
BM
=
1
2
DF.
延长
FE
与
CB
交于点
G
,
连接
AG
,
则易知
△
CEF
与
△
CEG
均为等腰直角三角形
,
∴
CE
=
EF
=
EG
,
CF
=
CG
,
∴
点
E
为
FG
中点
,
又点
M
为
AF
中点
,
∴
ME
=
1
2
AG.
在
△
ACG
与
△
DCF
中
,
î
ï
í
ï
ì
AC
=
CD
∠
ACG
=
∠
DCF
=
45
°
CG
=
CF
,
∴△
ACG
≌△
DCF
(
SAS
)
,
∴
DF
=
AG
,
∴
BM
=
ME
证法二:如图
⑤
,
延长
BM
交
CF
于点
D
,
连接
BE
,
DE
,
∵∠
BCE
=
45
°
,
∴∠
ACD
=
45
°
×
2
+
45
°
=
135
°
,
∴∠
BAC
+
∠
ACF
=
45
°
+
135
°
=
180
°
,
∴
AB
∥
CF
,
∴∠
BAM
=
∠
DFM
,
∴
M
是
AF
的中点
,
∴
AM
=
FM
,
在
△
ABM
和
△
FDM
中
,
î
í
ì
∠
BAM
=
∠
DFM
,
AM
=
FM
,
∠
AMB
=
∠
FMD
,
∴△
ABM
≌△
FDM
(
ASA
)
,
∴
AB
=
DF
,
BM
=
DM
,
∴
AB
=
BC
=
DF
,
∵
在
△
BCE
和
△
DFE
中
,
î
í
ì
BC
=
DF
,
∠
BCE
=
∠
DFE
=
45
°
,
CE
=
FE
,
∴△
BCE
≌△
DFE
(
SAS
)
,
∴
BE
=
DE
,
∠
BEC
=
∠
DEF
,
∴∠
B
ED
=
∠
BEC
+
∠
CED
=
∠
DEF
+
∠
CED
=
∠
CEF
=
90
°
,
∴△
BDE
是等腰直角三角
形
,
又
∵
BM
=
DM
,
∴
BM
=
ME
=
1
2
BD
,
故
BM
=
ME
相关文档
- 中考数学复习专题十:代数总复习2021-11-1010页
- 鄂尔多斯专版2020中考数学复习方案2021-11-1010页
- 呼和浩特专版2020中考数学复习方案2021-11-107页
- 鄂尔多斯专版2020中考数学复习方案2021-11-1011页
- 【中考数学复习,PPT课件】初中数学2021-11-1016页
- 中考数学复习专题十四:几何与函数问2021-11-1014页
- 中考数学复习:将军饮马问题课件-352021-11-1035页
- 呼和浩特专版2020中考数学复习方案2021-11-1017页
- 福建专版2020中考数学复习方案第三2021-11-108页
- 福建专版2020中考数学复习方案第一2021-11-107页