呼和浩特专版2020中考数学复习方案第七单元图形的变化第30课时平移与旋转课件 37页

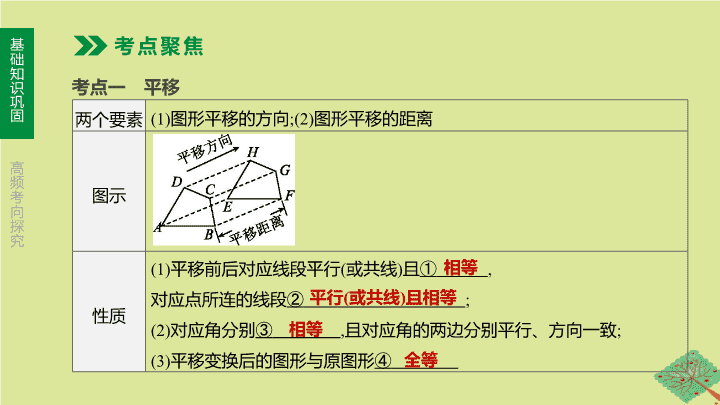
第 30 课时　 平移与旋转 第七单元　图形的变化 两个要素 (1) 图形平移的方向 ;(2) 图形平移的距离 图示 性质 (1) 平移前后对应线段平行 ( 或共线 ) 且 ① 　　　 , 对应 点所连的线段 ② 　　 　　 ;  (2) 对应角分别 ③ 　　　　 , 且对应角的两边分别平行、方向一致 ;  (3) 平移变换后的图形与原图形 ④ 　　   考点一　平移 考点聚焦 相等 平行 ( 或共线 ) 且相等 相等 全等 ( 续表 ) 网格作图 的步骤 　 (1) 确定平移方向和平移距离 ; 　 ( 2) 找原图形关键点 ; 　 ( 3) 按平移方向和距离平移各关键点 ; 　 ( 4) 按原图形顺次连接各关键点平移后的对应点 , 得到平移后的图形 三个要素 (1) 旋转中心 ;(2) 旋转方向 ;(3) 旋转角度 图示 性质 (1) 对应点到旋转中心的距离 ⑤ 　　　 ;  (2) 对应点与旋转中心所连线段的夹角等于 ⑥ 　　　　 ;  (3) 旋转前后的图形 ⑦ 　　　   考点二　旋转 相等 旋转角 全等 ( 续表 ) 网格作图 的步骤 (1) 确定旋转中心、旋转方向及旋转角 ; ( 2) 找原图形的关键点 ; ( 3) 连接关键点与旋转中心 , 按旋转方向与旋转角将它们旋转 , 得到各关键点的对应点 ; ( 4) 按原图形依次连接各关键点的对应点 , 得到旋转后的图形 【 温馨提示 】 旋转对称与中心对称的关系 : 中心对称是旋转角为 180 ° 的旋转对称 . 题组一　必会题 对点演练 1 . 将点 A (-5,-2) 向右平移 3 个单位长度得到点 B , 则点 B 所在的象限是 ( 　　 ) A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限 2 . 将数字 “6” 旋转 180°, 得到数字 “9”, 将数字 “9” 旋转 180°, 得到数字 “6”, 现将数字 “96” 旋转 180°, 得到的数字是 ( 　　 ) A . 96 B . 69 C . 66 D . 99 C A 3 . 在网格图 30-1 中 , 每个小正方形的边长均为 1,△ ABC 的三个顶点都是网格线的交点 , 已知 B , C 两点的坐标分别为 (-1,-1),(1,-2), 将 △ ABC 绕点 C 顺时针旋转 90°, 则点 A 的对应点的坐标为 ( 　　 ) A . (4,1) B . (4,-1) C . (5,1) D . (5,-1) 图 30-1 [ 答案 ] D 　 [ 解析 ] 根据 B , C 的坐标可确定直角坐标系的原点 , 由旋转的性质可知 , 点 A 绕着点 C 顺时针旋转 90° 后的坐标为 (5,-1) . 故选 D . 4 . [ 九上 P63 习题 23 . 1 第 9 题改编 ] 如图 30-2, △ ABC 中 , ∠ C= 90° . 将 △ ABC 绕点 B 逆时针旋转 90°, 若 BC= 3, AC= 4, 点 A 旋转后的对应点为 A' , 则 A'A 的长为 　　　　 .  图 30-2 5 . [ 九上 P62 习题 23 . 1 第 4 题 ] 分别画出 △ ABC 绕点 O 逆时针旋转 90° 和 180° 后的图形 . 图 30-3 解 : 如图所示 . 题组二　易错题 【 失分点 】 对于图形旋转变换后出现的新结论挖掘不彻底 ; 有关相似三角形面积比与相似比之间的关系在运用时出错 ; 需明确与三点共线有关的最值问题 ; 缺乏利用作图辅助分析解决问题的能力 . 6 . 如图 30-4, 在正方形 ABCD 中 , 点 E , F 分别在 BC , CD 上 , 且∠ EAF= 45°, 将三角形 ABE 绕点 A 顺时针旋转 90°, 使点 E 落在点 E' 处 , 则下列判断不正确的是 ( 　　 ) A . △ AEE' 是等腰直角三角形 B .AF 垂直平分 EE' C . △ E'EC ∽△ AFD D . △ AE'F 是等腰三角形 图 30-4 [ 答案 ] D 　 [ 解析 ] ∵将 △ ABE 绕点 A 顺时针旋转 90°, 使点 E 落在点 E' 处 , ∴ AE'=AE , ∠ E'AE= 90°, ∴ △ AEE' 是等腰直角三角形 , 故 A 正确 ; ∵将 △ ABE 绕点 A 顺时针旋转 90°, 使点 E 落在点 E' 处 , ∴∠ E'AD= ∠ BAE. ∵四边形 ABCD 是正方形 , ∴∠ DAB= 90° . ∵∠ EAF= 45°, ∴∠ BAE + ∠ DAF= 45°, ∴∠ E'AD + ∠ FAD= 45°, ∴∠ E'AF= ∠ EAF. ∵ AE'=AE , ∴ AF 垂直平分 EE' , 故 B 正确 ; ∵ AF ⊥ E'E , ∠ ADF= 90°, ∴∠ FE'E + ∠ AFD= ∠ AFD + ∠ DAF , ∴∠ FE'E= ∠ DAF , ∴ △ E'EC ∽△ AFD , 故 C 正确 ; ∵ AD ⊥ E'F , 但∠ E'AD 不一定等于∠ DAF , ∴ △ AE'F 不一定是等腰三角形 , 故 D 错误 . 图 30-5 D 考向一　与平移有关的计算 例 1 如图 30-6,△ A 1 B 1 C 1 是 △ ABC 向右平移 4 个单位长度后得到的 , 且三个顶点的坐标分别为 A 1 (1,1), B 1 (4,2), C 1 (3,4) . (1) 请画出 △ ABC , 并写出点 A , B , C 的坐标 ; (2) 求出 △ AOA 1 的面积 . 图 30-6 【 方法点析 】 (1) 对应点间的距离等于平移的距离 ; (2) 利用 “ 平移前后的两个图形全等 ”“ 平移前后对应线段平行 ( 或在同一条直线上 ) 且相等 ” 是解决平移问题的基本方法 . | 考向精练 | 1 . [2019· 呼和浩特一模 ] 如图 30-7 所示 , 在平面直角坐标系中 , 点 A , B , C 的坐标分别为 (-1,3) 、 (-4,1) 、 (-2,1), 将 △ ABC 沿一确定方向平移得到 △ A 1 B 1 C 1 , 点 B 的对应点 B 1 的坐标是 (1,2), 则点 C 对应的点 C 1 的坐标是 ( 　　 ) A . (3,2) B . (2,1) C . (2,3) D . (2,2) A 图 30-7 2 . [2014· 呼和浩特 3 题 ] 已知线段 CD 是由线段 AB 平移得到的 , 点 A (-1,4) 的对应点为 C (4,7), 则点 B (-4,-1) 的对应点 D 的坐标为 ( 　　 ) A . (1,2) B . (2,9) C . (5,3) D . (-9,-4) [ 答案 ] A 　 [ 解析 ] ∵点 A (-1,4) 的对应点为 C (4,7), ∴平移规律为向右平移 5 个单位 , 向上平移 3 个单位 , ∵点 B (-4,-1), ∴点 D 的坐标为 (1,2) . 故选 :A . 3 . 如图 30-8, 将周长为 8 的 △ ABC 沿 BC 方向向右平移 1 个单位长度得到 △ DEF , 则四边形 ABFD 的周长为 ( 　　 ) A . 6 B . 8 C . 10 D . 12 图 30-8 [ 答案 ] C 　 [ 解析 ] 将周长为 8 的 △ ABC 沿边 BC 向右平移 1 个单位长度得到 △ DEF , ∴ AD= 1, BF=BC + CF=BC +1, DF=AC. 又∵ AB + BC + AC= 8, ∴四边形 ABFD 的周长 =AD + AB + BF + DF = 1+ AB + BC +1+ AC= 10 . 4 . [2018· 呼和浩特 20 题 ] 如图 30-9, 已知 A (6,0), B (8,5), 将线段 OA 平移至 CB , 点 D 在 x 轴正半轴上 ( 不与点 A 重合 ), 连接 OC , AB , CD , BD. (1) 求对角线 AC 的长 ; (2) 设点 D 的坐标为 ( x ,0),△ ODC 与 △ ABD 的面积分别记为 S 1 , S 2 , 设 S=S 1 - S 2 , 写出 S 关于 x 的函数解析式 , 并探究是否存在点 D 使 S 与 △ DBC 的面积相等 , 如果存在 , 用坐标形式写出点 D 的位置 ; 如果不存在 , 说明理由 . 图 30-9 4 . [2018· 呼和浩特 20 题 ] 如图 30-9, 已知 A (6,0), B (8,5), 将线段 OA 平移至 CB , 点 D 在 x 轴正半轴上 ( 不与点 A 重合 ), 连接 OC , AB , CD , BD. (2) 设点 D 的坐标为 ( x ,0),△ ODC 与 △ ABD 的面积分别记为 S 1 , S 2 , 设 S=S 1 - S 2 , 写出 S 关于 x 的函数解析式 , 并探究是否存在点 D 使 S 与 △ DBC 的面积相等 , 如果存在 , 用坐标形式写出点 D 的位置 ; 如果不存在 , 说明理由 . 图 30-9 考向二　与旋转有关的证明与计算 图 30-10 [ 答案 ] C | 考向精练 | 图 30-11 1 . [2019· 吉林 ] 把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合 , 则这个旋转角度至少为 ( 　　 ) A . 30° B . 90° C . 120° D . 180° C 图 30-12 [ 答案 ] D 　 [ 解析 ] 根据旋转的性质可知 : AC=AC' , ∠ C'AC= 60°, ∴ △ ACC' 为等边三角形 , ∴∠ ACB= 60°, ∴∠ AC'B'= ∠ C= 60°, ∵ C' 为 BC 的中点 , ∴ BC'=C'C=AC‘ , ∴∠ B= ∠ BAC'= 30°, ∴∠ BDC'= ∠ C'AB + ∠ AC'B'= 90°, 即 B'C' ⊥ AB , ∴ BC'= 2 C'D , ∴ BC=B'C'= 4 C'D , ∴ C'D ∶ DB'= 1 ∶ 3 . 故选 D . 3 . [2019· 益阳 ] 在如图 30-13 所示的方格纸 (1 格长为 1 个单位长度 ) 中 ,△ ABC 的顶点都在格点上 , 将 △ ABC 绕点 O 按顺时针方向旋转得到 △ A'B'C' , 使各顶点仍在格点上 , 则其旋转角的度数是 　　　　 .  图 30-13 90° 图 30-14 图 30-14 图 30-14