2018年吉林省中考数学试卷含答案 12页

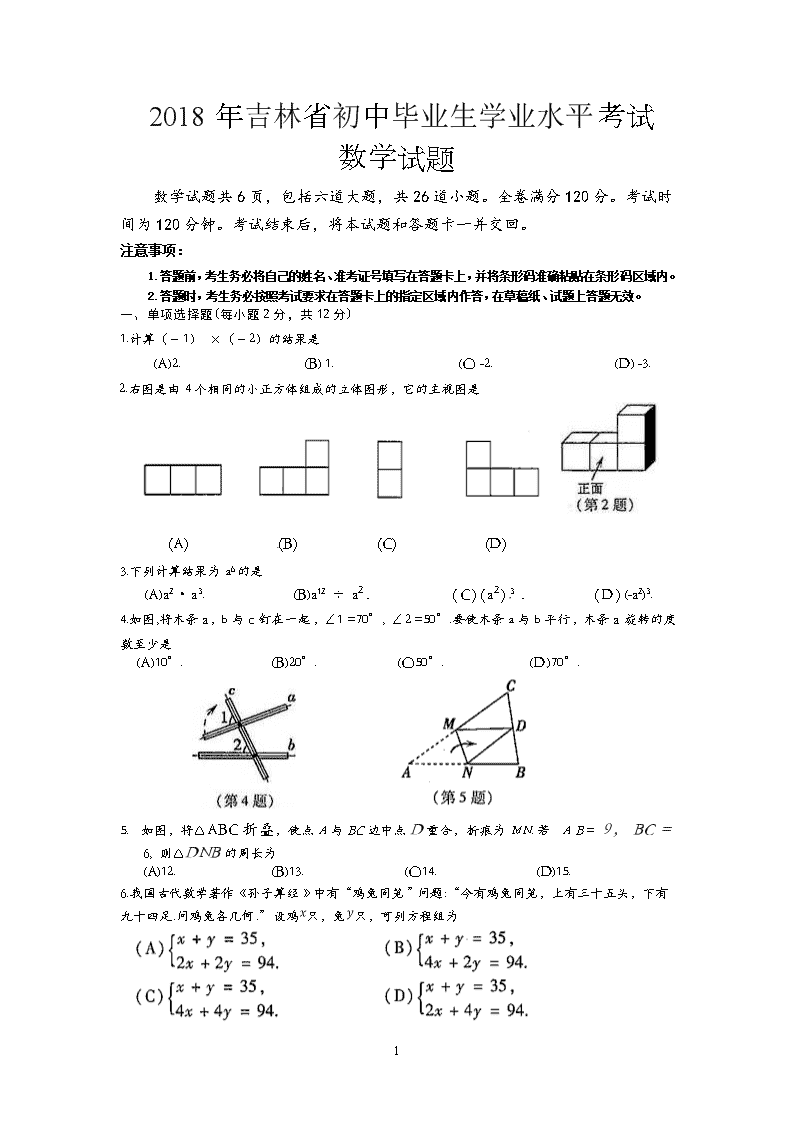
‎2018年吉林省初中毕业生学业水平考试 数学试题 数学试题共6页，包括六道大题，共26道小题。全卷满分120分。考试时间为120分钟。考试结束后，将本试题和答题卡一并交回。‎ 注意事项： ‎ ‎1.答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形码区域内。‎ ‎2.答题时，考生务必按照考试要求在答题卡上的指定区域内作答，在草稿纸、试题上答题无效。[来源:学_科_网Z_X_X_K]‎ 一、单项选择题(每小题2分，共12分)‎ ‎1.计算（﹣1） ×（﹣2）的结果是 ‎(A)2. (B) 1. (C) -2. (D) -3.‎ ‎2.右图是由4个相同的小正方体组成的立体图形，它的主视图是 (A) ‎ (B) (C) (D)‎ ‎3.下列计算结果为a6的是 ‎(A)a2 • a3. (B)a12 ÷ a2. (C)(a2)3 . (D)(-a2)3.‎ ‎4.如图,将木条a，b与c钉在一起，∠1 =70°, ∠2 =50°.要使木条a与b平行，木条a旋转的度数至少是 ‎(A)10°. (B)20°. (C)50°. (D)70°.‎ ‎ ‎ 5. 如图，将△ABC折叠，使点A与BC边中点D重合，折痕为MN.若AB= 9，BC = 6, 则△DNB的周长为 ‎ (A)12. (B)13. (C)14. 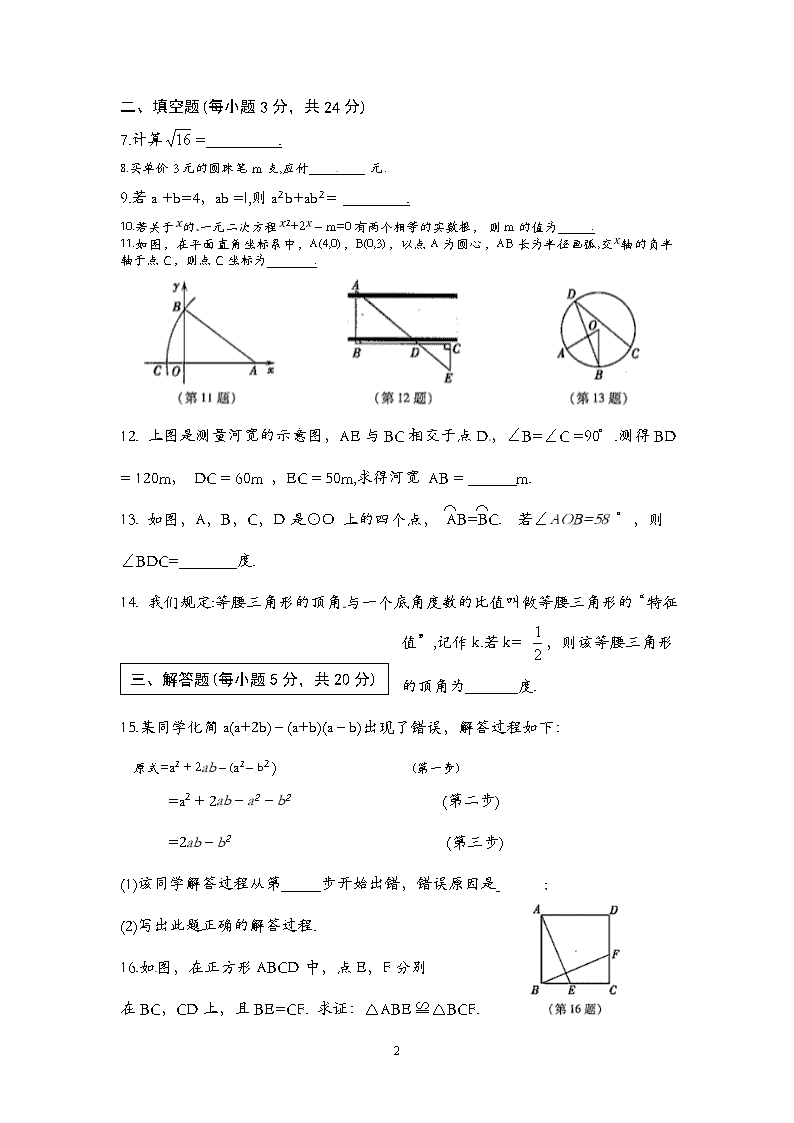(D)15.‎ ‎6.我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼，上有三十五头，下有九十四足.问鸡兔各几何.”设鸡只，兔只，可列方程组为 ‎ ‎ ‎ 12‎ 二、填空题(每小题3分，共24分)‎ ‎7.计算= .‎ ‎8.买单价3元的圆珠笔m支,应付 元.‎ ‎9.若a +b=4，ab =l,则a2 b+ab2 = .‎ ‎10.若关于的一元二次方程2+2﹣m=0有两个相等的实数根，则m的值为 .‎ ‎11.如图，在平面直角坐标系中，A(4,0)，B(0,3)，以点A为圆心，AB长为半径画弧,交轴的负半轴于点C，则点C坐标为 .‎ ‎⌒ ⌒‎ 12. 上图是测量河宽的示意图，AE与BC相交于点D，∠B=∠C =90°.测得BD = 120m， DC = 60m ，EC = 50m,求得河宽 AB = m.‎ 13. 如图，A，B，C，D是⊙O 上的四个点， AB=BC. 若∠AOB=58 °，则 ‎∠BDC= 度.‎ 14. 我们规定:等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”,记作k.若k= ，则该等腰三角形的顶角为 度.‎ 三、解答题(每小题5分，共20分)‎ ‎15.某同学化简a(a+2b)﹣(a+b)(a﹣b)出现了错误，解答过程如下：‎ 原式=a2 + 2ab﹣(a2﹣b2) (第一步)‎ ‎=a2 + 2ab﹣a2﹣b2 (第二步)‎ ‎ =2ab﹣b2 (第三步)‎ ‎(1)该同学解答过程从第 步开始出错，错误原因是 ;‎ ‎(2)写出此题正确的解答过程. ‎ ‎16.如图，在正方形ABCD中，点E，F分别 ‎ 在BC，CD上，且BE=CF. 求证：△ABE ≌△BCF.‎ 12‎ 17. 一个不透明的口袋中有三个小球,上面分别标有字母A，B，C，除所标字母不同外，其它完全相同.从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球. 用画树状图(或列表)的方法，求该同学两次摸出的小球所标字母相同的概率.‎ 四、解答题(每小题7分，共28分)‎ 18. 在平面直角坐标系中，反比例函数y=(k≠0)图象与一次函数y=x+2图象的一个交点为P,且点P的横坐标为1，求该反比例函数的解析式.‎ 19. 下图是学习分式方程应用时，老师板书的问题和两名同学所列的方程.‎ ‎ ‎ 根据以上信息，解答下列问题。‎ （1） ‎ 冰冰同学所列方程中的表示 ‎ 庆庆同学所列方程中的表示 ；‎ ‎（2）两个方程中任选一个，并写出它的等量关系；‎ ‎（3）解(2)中你所选择的方程，并回答老师提出的问题。‎ 20. 下图是由边长为1的小正方形组成的8 × 4网格，每个小正方形的顶点叫做格点.点A，B，C，D均在格点上，在网格中将点D按下列步骤移动: ‎ 第一步：点D绕点A顺时针旋转180°得到点D;‎ 笫二步: 点D绕点B顺时针旋转90°得到点D2 ;‎ 笫三步: 点D2绕点C顺时针旋转90°回到点D .‎ ‎（1）请用圆规画出点D → D→ D2 → D 经过的路径；[来源:学科网ZXXK]‎ ‎ （2）所画图形是 对称图形；‎ ‎ （3）求所画图形的周长（结果保留π）‎ ‎21.数学活动小组的同学为测量旗杆高度，先制定了如下测量方案，使用工具是测角仪和皮尺，请帮助组长林平完成方案内容，用a,b,α的代数式表示旗杆AB的高度.‎ 12‎ ‎ 数学活动方案 ‎ ‎ 活动时间2018年4月2 日 活动地点：学校操场 填表人：林平；‎ 课题 测量学校旗杆的高度 活动目的 运用所学数学知识及方法解决实际问题 方案示意图 测量步骤 ‎（1）用 测得 ‎∠ADE= α；‎ ‎（2）用 测得 BC=a 米，CD=b米.‎ 计算过程 ‎ [来源:学科网ZXXK]‎ ‎ 22.为了调査甲、乙两台包装机分装标准质量为400g奶粉的情况，质检员进行了抽样调查，过程如下.请补全表一、表二中的空白，并回答提出的问题.‎ 收集数据： ‎ 从甲、乙包装机分装的奶粉中各自随机抽取10袋，测得实际质量(单位:g)如下：‎ 甲： 400,400,408,406,410,409,400,393,394,395 ‎ 乙: 403,404,396,399,402,402,405,397, 402,398‎ 整理数据 分析数据： ‎ 表二 种类 平均数 中位数 众数 方差 甲 ‎401.5‎ ‎ ‎ ‎400‎ ‎36. 85‎ 乙 ‎400.8‎ ‎402‎ ‎ ‎ ‎8.56‎ 得出结论：‎ 包装机分装情况比较好的是 (填甲或乙)，说明你的理由。‎ ‎23.小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行.小玲开始跑步中途改为步行，到达图书馆恰好用30min.小东骑自行车以300m/min的速度直接回家.‎ 12‎ ‎ 两人离家的路程y(m)与各自离开出发地的时间(min)之间的函数图象如图所示.‎ ‎(1)家与图书馆之间的路程为 m,小玲步行的速度为 m/min；‎ ‎(2)求小东离家的路程关于的函数解析式，并写出自变量的取值范围；‎ ‎(3)求两人相遇的时间.‎ ‎ ‎ ‎24.如图①，在△ABC中,AB=AC，过AB上一点D作DE∥AC交BC于点E，以E为顶点, ED为一边，作∠DEF=∠A ，另一边EF交AC于点F.‎ ‎(1)求证:四边形ADEF为平行四边形；‎ ‎(2)当点D为AB 中点时，▱ADEF的形状为 　 ；‎ ‎(3)延长图①中的DE到点G,　使EＧ＝DE，连接AE,AG,FG得到图②‎ 若AD =AG, 判断四边形AEGF的形状，并说明理由. ‎ ‎25.如图，在矩形ABCD中,AB= 2cm,∠ADB =30°. P，Q两点分别从A，B同时出发，点P沿折线AB--BC运动，在AB上的速度是2cm/s,在BC上的速度是2cm/s;点Q在BD上以2cm/s的速度向终点D运动.过点P作PN⊥AD，垂足为点N.连接PQ，以PQ，PN 为邻边作▱PQMN.设运动的时间为(s)，▱PQMN与矩形ABCD重叠部分的图形面积为(cm2).‎ 12‎ ‎(1)当PQ⊥AB时， = 　 ；‎ ‎(2)求关于的函数解析式，并写出的取值范围；‎ ‎(3)直线AM将矩形ABCD的面积分成1:3两部分时，直接写出的值.‎ ‎[来源:学#科#网]‎ ‎26.如图，在平面直角坐标系中，抛物线=a2+2a﹣3a (a＜0)与轴相交于A，B两点，与轴相交于点C，顶点为D，直线DC与轴相交于点E.‎ ‎(1)当a= ﹣1时，抛物线顶点D的坐标为 　 ,OE = 　 ；‎ ‎(2)OE的长是否与a值有关，说明你的理由；‎ ‎(3)设∠DEO= β, 45°≤β≤ 60°，求a的取值范围；‎ ‎(4)以DE为斜边，在直线DE的左下方作等腰直角三角形PDE.设P（m,n）直接写出 n关于m的函数解析式及自变量m的取值范围.‎ ‎ ‎ 12‎ ‎ ‎ 12‎ 12‎ 12‎ 12‎ 12‎ ‎ ‎ 12‎