初中数学中考总复习课件PPT：17解直角三角形 19页

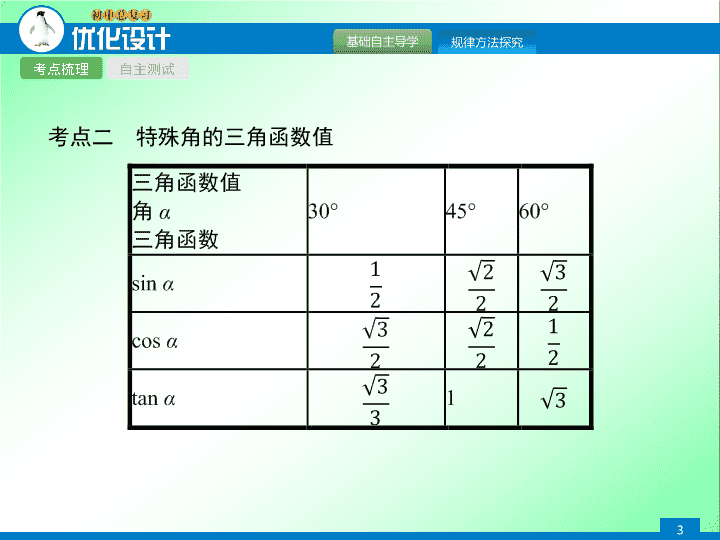
第 17 课时　解直角三角形 考点梳理 自主测试 考点一 　 锐角三角函数定义 在Rt △ ABC 中, ∠ C= 90°, ∠ A , ∠ B , ∠ C 的对边分别为 a , b , c. 考点梳理 自主测试 考点二 　 特殊角的三角函数值 考点梳理 自主测试 考点三 　 解直角三角形 1 . 解直角三角形的定义 由直角三角形中除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形 . 在直角三角形中,除直角外,一共有5个元素,即3条边和2个锐角 . 已知元素中,至少有一个是 边 的条件,才能解直角三角形 . 2 . 直角三角形的边角关系 在Rt △ ABC 中, ∠ C= 90°, ∠ A , ∠ B , ∠ C 的对边分别为 a , b , c. (1)三边之间的关系: a 2 +b 2 =c 2 ; (2)锐角之间的关系: ∠ A+ ∠ B= 90° ; 考点梳理 自主测试 考点梳理 自主测试 考点四 　 解直角三角形的应用 1 . 仰角与俯角 在进行观察时,从下向上看,视线与水平线的夹角叫 仰角 ;从上往下看,视线与水平线的夹角叫做 俯角 . 2 . 坡角与坡度 ( 坡比 ) 坡角是坡面与水平面所成的角;坡度是斜坡上两点 垂直高度 与水平距离之比,常用 i 表示,也就是坡角的正切值,坡角越大,坡度越大,坡面 越陡 . 考点梳理 自主测试 3 . 方向角 指北或指南方向线与目标方向线所成的小于90°的角叫做方向角 . 常见的方向角表示为北偏东多少度、北偏西多少度、南偏东多少度、南偏西多少度 . 如图,目标方向线 OA , OB , OC , OD 的方向角分别表示北偏东 30° 、南偏东 60° 、南偏西 80° 、北偏西 45° . 北偏西45°通常也叫 西北 方向 . 考 点 梳理 自主测试 1 . 如图 , 在 Rt △ ABC 中 , ∠ ACB= 90°, BC= 1, AB= 2, 则下列结论正确的是 ( 　　 ) 答案 : D 2 . 在正方形网格中 , △ ABC 的位置如图 , 则 cos B 的值为 ( 　　 ) 答案 : B 考 点 梳理 自主测试 3 . 如图 , AB 是 ☉ O 的直径 , C 是 ☉ O 上的点 , 过点 C 作 ☉ O 的切线交 AB 的延长线于点 E , 若 ∠ A= 30°, 则 sin ∠ E 的值为 ( 　　 ) 答案: A 4 . 如图,已知在Rt △ ABC 中, ∠ C= 90°, AB= 13, AC= 12,则cos B 的值为 　　　　 .  命题点 1 命题点 2 命题点 3 命题点 4 命题点 1 　 锐角三角函数的定义 答案 : B 命题点 1 命题点 2 命题点 3 命题点 4 命题点 1 命题点 2 命题点 3 命题点 4 命题点 2 　 特殊角的三角函数值 命题点 1 命题点 2 命题点 3 命题点 4 命题点 3 　 解直角三角形 命题点 1 命题点 2 命题点 3 命题点 4 命题点 1 命题点 2 命题点 3 命题点 4 命题点 1 命题点 2 命题点 3 命题点 4 命题点 4 　 解直角三角形在实际中的应用 【例 4 】 如图,在一次数学课外实践活动中,要求测教学楼的高度 AB. 小刚在 D 处用高1 . 5 m的测角仪 CD ,测得教学楼顶端 A 的仰角为30°,然后向教学楼前进40 m到达 E 处,又测得教学楼顶端 A 的仰角为60° . 求这幢教学楼的高度 AB. 命题点 1 命题点 2 命题点 3 命题点 4 命题点 1 命题点 2 命题点 3 命题点 4 变式训练 如图 , 某施工单位为测得某河段的宽度 , 测量员先在河对岸岸边取一点 A , 再在河这边沿河边取两点 B , C , 在点 B 处测得点 A 在北偏东 30° 方向上 , 在点 C 处测得点 A 在西北方向上 , 量得 BC 长为 200 m, 请你求出该河段的宽度 . ( 结果保留根号 ) 命题点 1 命题点 2 命题点 3 命题点 4 解 : 如图 , 过点 A 作 AD ⊥ BC 于点 D. 根据题意得 , ∠ ABD= 90° - 30° = 60°, ∠ ACD= 45° . ∴ ∠ CAD= 45°, ∴ ∠ ACD= ∠ CAD , ∴ AD=CD , ∴ BD=BC-CD= 200 -AD.