2021年中考数学压轴题专项训练 反比例函数（含解析） 24页

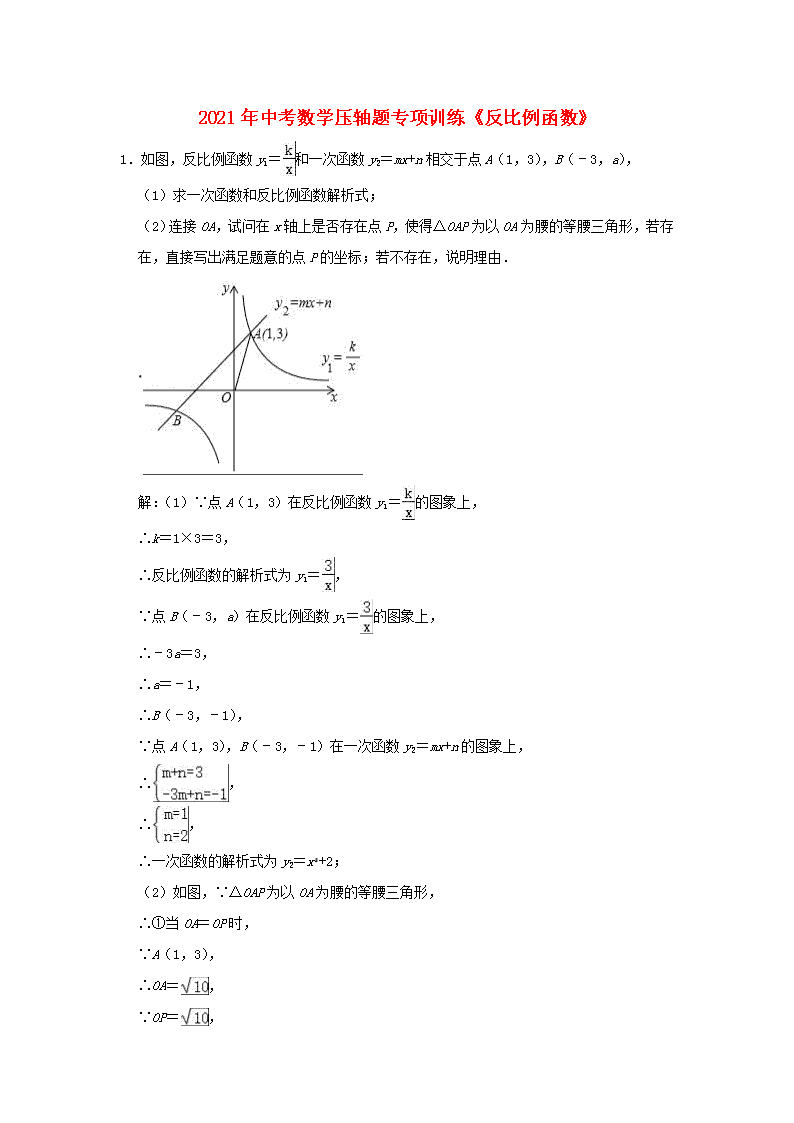
2021 年中考数学压轴题专项训练《反比例函数》 1．如图，反比例函数 y1＝ 和一次函数 y2＝mx+n 相交于点 A（1，3），B（﹣3，a）， （1）求一次函数和反比例函数解析式； （2）连接 OA，试问在 x 轴上是否存在点 P，使得△OAP 为以 OA 为腰的等腰三角形，若存 在，直接写出满足题意的点 P 的坐标；若不存在，说明理由． 解：（1）∵点 A（1，3）在反比例函数 y1＝ 的图象上， ∴k＝1×3＝3， ∴反比例函数的解析式为 y1＝ ， ∵点 B（﹣3，a）在反比例函数 y1＝ 的图象上， ∴﹣3a＝3， ∴a＝﹣1， ∴B（﹣3，﹣1）， ∵点 A（1，3），B（﹣3，﹣1）在一次函数 y2＝mx+n 的图象上， ∴ ， ∴ ， ∴一次函数的解析式为 y2＝x +2； （2）如图，∵△OAP 为以 OA 为腰的等腰三角形， ∴①当 OA＝OP 时， ∵A（1，3）， ∴OA＝ ， ∵OP＝ ， ∵点 P 在 x 轴上， ∴P（﹣ ，0）或（ ，0）， ②当 OA＝AP 时，则点 A 是线段 OP 的垂直平分线上， ∵A（1，3）， ∴P（2，0）， 即：在 x 轴上存在点 P，使得△OAP 为以 OA 为腰的等腰三角形，此时，点 P 的坐标为（﹣ ，0）或（2，0）或（ ，0）． 2．在平面直角坐标系 xOy 中，函数 y＝ （x＞0）的图象 G 经过点 A（3，2），直线 l：y＝ kx﹣1（k≠0）与 y 轴交于点 B，与图象 G 交于点 C． （1）求 m 的值； （2）横、纵坐标都是整数的点叫做整点．记图象 G 在点 A，C 之间的部分与线段 BA，BC 围成的区域（不含边界）为 W． ①当直线 l 过点（2，0）时，直接写出区域 W 内的整点个数； ② 若区域 W 内的整点不少于 4 个，结合函数图象，求 k 的取值范围． 解：（1）把 A（3，2）代入 y＝ 得 m＝3×2＝6， （2）①当直线 l 过点（2，0）时，直线解析式为 y＝ x﹣1， 解方程 ＝ x﹣1 得 x1＝1﹣ （舍去），x2＝1+ ，则 C（1+ ， ）， 而 B（0，﹣1）， 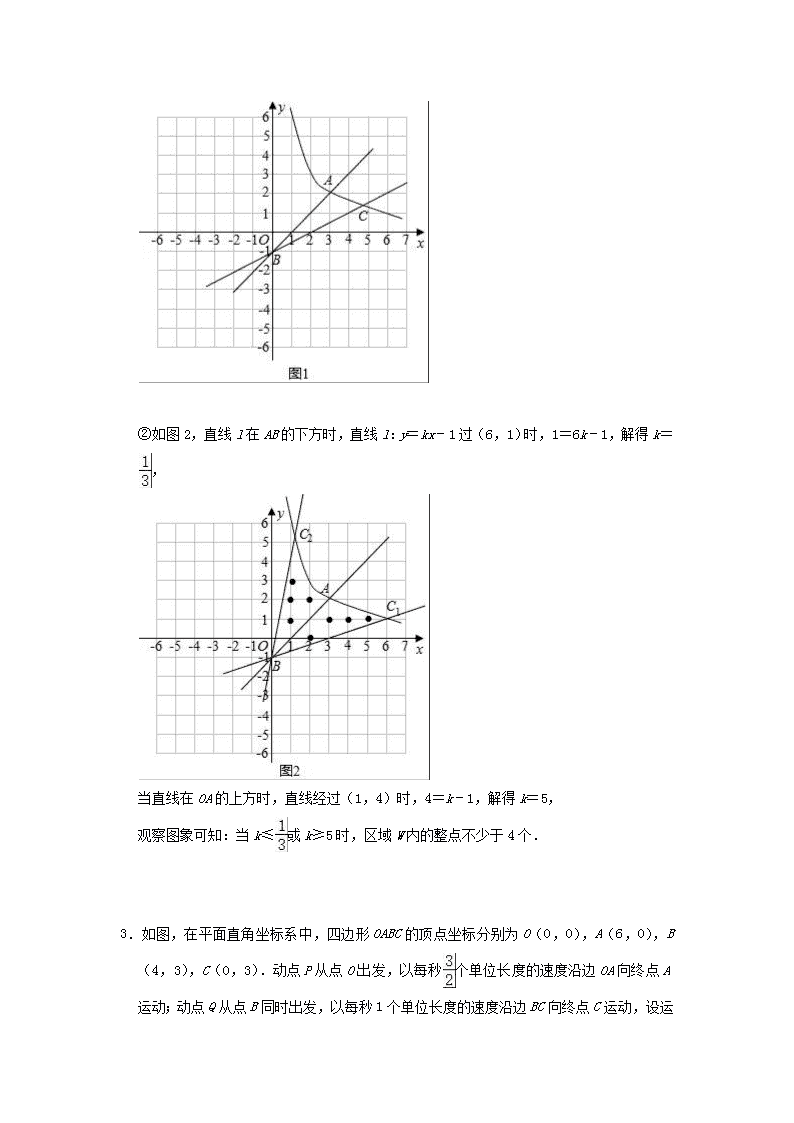如图 1 所示，区域 W 内的整点有（3，1）一个； ②如图 2，直线 l 在 AB 的下方时，直线 l：y＝kx﹣1 过（6，1）时，1＝6k﹣1，解得 k ＝ ， 当直线在 OA 的上方时，直线经过（1，4）时，4＝k﹣1，解得 k＝5， 观察图象可知：当 k≤ 或 k≥5 时，区域 W 内的整点不少于 4 个． 3．如图，在平面直角坐标系中，四边形 OABC 的顶点坐标分别为 O（0，0），A（6，0），B（4， 3），C（0，3）．动点 P 从点 O 出发，以每秒 个单位长度的速度沿边 OA 向终点 A 运动； 动点 Q 从点 B 同时出发，以每秒 1 个单位长度的速度沿边 BC 向终点 C 运动，设运动的时 间为 t 秒，PQ2＝y． （ 1 ） 直 接 写 出 y 关 于 t 的 函 数 解 析 式 及 t 的 取 值 范 围 ： ； （2）当 PQ＝ 时，求 t 的值； （3）连接 OB 交 PQ 于点 D，若双曲线 y＝ 经过点 D，问 k 的值是否变化？若不 变化，请求出 k 的值；若变化，请说明理由． 解：（1）过点 P 作 PE⊥BC 于点 E，如图 1 所示． 当运动时间为 t 秒时（0≤t≤4）时，点 P 的坐标为（ t，0），点 Q 的坐标为（4﹣t，3）， ∴PE＝3，EQ＝|4﹣t﹣ t|＝|4﹣ t|， ∴PQ2＝PE2+EQ2＝32+|4﹣ t|2＝ t2﹣20t+25， ∴y 关于 t 的函数解析式及 t 的取值范围： ； 故答案为： ． （2）当 时， 整理，得 5t2﹣16t+12＝0， 解得：t1＝2， ． （3）经过点 D 的双曲线 的 k 值不变． 连接 OB，交 PQ 于点 D，过点 D 作 DF⊥OA 于点 F，如图 2 所示． ∵OC＝3，BC＝4， ∴ ． ∵BQ∥OP， ∴△BDQ∽△ODP， ∴ ， ∴OD＝3． ∵CB∥OA， ∴∠DOF＝∠OBC． 在 Rt△OBC 中， ， ， ∴ ， ， ∴点 D 的坐标为 ， ∴经过点 D 的双曲线 的 k 值为 ． 4．如图，一次函数 y＝kx+b 的图象与反比例函数 y＝ 的图象交于点 A（﹣3，m+8），B（n， ﹣6）两点． （1）求一次函数与反比例函数的解析式； （2）求△AOB 的面积； （3）若 P（x1，y1） ，Q（x2，y2）是该反比例函数图象上的两点，且当 x1＜x2 时，y1＞y2， 指出点 P、Q 各位于哪个象限？ 解：（1）将 A（﹣3，m+8）代入反比例函数 y＝ 得﹣3（m+8）＝m，解得 m＝﹣6， ∴点 A 的坐标为（﹣3，2），反比例函数解析式为 y＝﹣ ， 将点 B（n，﹣6）代入 y＝﹣ 得﹣6n＝﹣6，解得 n＝1， ∴点 B 的坐标为（1，﹣6）， 将点 A（﹣3，2），B（1，﹣6）代入 y＝kx+b 得 ，解得 ， ∴一次函数解析式为 y＝﹣2x﹣4； （2）设 AB 与 x 轴相交于点 C，如图， 当﹣2x﹣4＝0，解得 x＝﹣2，则点 C 的坐标为（﹣2，0）， ∴S△AOB＝S△AOC+S△BOC， ＝ ×2×2+ ×2×6， ＝2+6， ＝8； （3）∵当 x1＜x2 时，y1＞y2， ∴点 P 和点 Q 不在同一象限， ∴P 在第二象限，Q 在第四象限． 5．如图，平面直角坐标系中，一次函数 y＝x﹣1 的图象与 x 轴，y 轴分别交于点 A，B，与 反比例函数 y＝ 的图象交于点 C，D，CE⊥x 轴于点 E， ＝ ． （1）求反比例函数的表达式与点 D 的坐标； （2）以 CE 为边作▱ ECMN，点 M 在一次函数 y＝x﹣1 的图象上，设点 M 的横坐标为 a，当 边 MN 与反比例函数 y＝ 的图象有公共点时，求 a 的取值范围． 解：（1）由题意 A（1，0），B（0，﹣1）， ∴OA＝OB＝1， ∴∠OAB＝∠CAE＝45° ∵AE＝3OA， ∴AE＝3， ∵EC⊥x 轴， ∴∠AEC＝90°， ∴∠EAC＝∠ACE＝45°， ∴EC＝AE＝3， ∴C（4，3）， ∵反比例函数 y＝ 经过点 C（4，3）， ∴k＝12， 由 ，解得 或 ， ∴D（﹣3，﹣4）． （2）如图，设 M（a，a﹣1）． 当点 N 在反比例函数的图象上时，N（a， ）， ∵四边形 ECMN 是平行四边形， ∴MN＝EC＝3， ∴|a﹣1﹣ |＝3， 解得 a＝6 或﹣2 或﹣1± （舍弃）， ∴M（6，5）或（﹣2，﹣3）， 观察图象可知：当边 MN 与反比例函数 y＝ 的图象有公共点时 4＜a≤6 或﹣3≤a≤﹣2． 6．如图，一次函数 y＝kx+2 的图象与 y 轴交于点 A，正方形 ABCD 的顶点 B 在 x 轴上，点 D 在直线 y＝kx+2 上，且 AO＝OB，反比例函数 y＝ （x＞0）经过点 C． （1）求一次函数和反比例函数的解析式； （2）点 P 是 x 轴上一动点，当△PCD 的周长最小时，求出 P 点的坐标； （3）在（2）的 条件下，以点 C、D、P 为顶点作平行四边形，直接写出第四个顶点 M 的 坐标． 解：（1）设一次函数 y＝kx+2 的图象与 x 轴交于点 E，连接 BD，如图 1 所示． 当 x＝0 时，y＝kx+2＝2， ∴OA＝2． ∵四边形 ABCD 为正方形，OA＝OB， ∴∠BAE＝90°，∠OAB＝∠OBA＝45°， ∴∠OAE＝∠OEA＝45°， ∴OE＝2，点 E 的坐标为（﹣2，0）． 将 E（﹣2，0）代入 y＝kx+2，得：﹣2k+2＝0，解得：k＝1， ∴一次函数的解析式为 y＝x+2． ∵∠OBD＝∠ABD+∠OBA＝90°， ∴BD∥OA． ∵OE＝OB＝2， ∴BD＝2OA＝4， ∴点 D 的坐标为（2，4）． ∵四边形 ABCD 为正方形， ∴点 C 的坐标为（2+2﹣0，0+4﹣2），即（4，2）． ∵反比例函数 y＝ （x＞0）经过点 C， ∴n＝4×2＝8， ∴反比例函数解析式为 y＝ ． （2）作点 D 关于 x 轴的对称点 D′，连接 CD′交 x 轴于点 P，此时△PCD 的周长取最小 值，如图 2 所示． ∵点 D 的坐标为（2，4）， ∴点 D′的坐标为（2，﹣4）． 设直线 CD′的解析式为 y＝ax+b（a≠0）， 将 C（4，2），D′（2，﹣4）代入 y＝ax+b，得： ， 解得： ， ∴直线 CD′的解析式为 y＝3x﹣10． 当 y＝0 时，3x﹣10＝0，解得：x＝ ， ∴当△PCD 的周长最小时，P 点的坐标为（ ，0）． （3）设点 M 的坐标为（x，y），分三种情况考虑，如图 3 所示． ①当 DP 为对角线时， ， 解得： ， ∴点 M1 的坐标为（ ，2）； ②当 CD 为对角线时， ， 解得： ， ∴点 M2 的坐标为（ ，6）； ③当 CP 为对角线时， ， 解得： ， ∴点 M3 的坐标为（ ，﹣2）． 综上所述：以点 C、 D、P 为顶点作平行四边形，第四个顶点 M 的坐标为（ ，2），（ ， 6）或（ ，﹣2）． 7．如图在平面直角坐标系中，一次函数 y＝﹣2x﹣4 的图象与反比例函数 y＝ 的图象交于 点 A（1，n），B（m，2） （1）求反比例函数关系式及 m 的值； （2）若 x 轴正半轴上有一点 M 满足△MAB 的面积为 16，求点 M 的坐标； （3）根据函数图象直接写出关于 x 的不等式在 ＜﹣2x﹣4 的解集 解：（1）∵一次函数 y＝﹣2x﹣4 的图象过点 A（1，n），B（m，2） ∴n＝﹣2﹣4，2＝﹣2m﹣4 ∴n＝﹣6 ，m＝﹣3， ∴A（1，﹣6） 把 A（1，﹣6）代入 y＝ 得，k＝﹣6， ∴反比例函数关系式为 y＝﹣ ； （2）设直线 AB 与 x 轴交于 N 点，则 N（﹣2，0）， 设 M（m，0），m＞0， ∵S△MAB＝S△BMN+S△AMN，△MAB 的面积为 16， ∴ |m+2|×（2+6）＝16， 解得 m＝2 或﹣6（不合题意舍去）， ∴M（2，0）； （3）由图象可知：不等式在 ＜﹣2x﹣4 的解集是 x＜﹣3 或 0＜x＜1． 8．如图，在平面直角坐标系中，点 A（3，5）与点 C 关于原点 O 对称，分别过点 A、C 作 y 轴的平行线，与反比例函数 的图象交于点 B、D，连结 AD、BC，AD 与 x 轴交于点 E（﹣2，0）． （1）求直线 AD 对应的函数关系式； （2）求 k 的值； （3）直接写出阴影部分图形的面积之和． 解：（1）设直线 AD 对应的函数关系式为 y＝ax+b． ∵直线 AD 过点 A（3，5），E（﹣2，0）， ∴ 解得 ∴直线 AD 的解析式为 y＝x+2． （2）∵点 A（3，5）关于原点 O 的对称点为点 C， ∴点 C 的坐标为（﹣3，﹣5）， ∵CD∥y 轴， ∴设点 D 的坐标为（﹣3，a）， ∴a＝﹣3+2＝﹣1， ∴点 D 的坐标为（﹣3，﹣1）， ∵反比例函数 y＝ 的图象经过点 D， ∴k＝﹣3×（﹣1）＝3； （3）如图： ∵点 A 和点 C 关于原点对称， ∴阴影部分的面积等于平行四边形 CDGF 的面积， ∴S 阴影＝4×3＝12． 9．如图，一次函数 y＝kx+b 的图象分别与反比例函数 y＝ 的图象在第一象限交于点 A（4， 3），与 y 轴的负半轴交于点 B，且 OA＝OB． （1）求函数 y＝kx+b 和 y＝ 的表达式； （2）已知点 C（0，8），试在该一次函数图象上确定一点 M，使得 MB＝MC，求此时点 M 的坐标． 解：（1）把点 A（4，3）代入函数得：a＝3×4＝12， ∴y＝ ， OA＝5， ∵OA＝OB， ∴OB＝5， ∴点 B 的坐标为（0，﹣5）， 把 B（0，﹣5），A（4，3）代入 y＝kx+b 得： ∴y＝2x﹣5； （2）作 MD⊥y 轴． ∵点 M 在一次函数 y＝2x﹣5 上， ∴设点 M 的坐标为（x，2x﹣5）． ∵MB＝MC， ∴CD＝BD， ∴x2+（8﹣2x+5）2＝x2+（﹣5﹣2x+5）2 ∴8﹣（2x﹣5）＝2x﹣5+5 解得：x＝ ∴2x﹣5＝ ， ∴点 M 的坐标为（ ， ）． 10．如图，矩形 OABC 的顶点 A、C 分别在 x、y 轴的正半轴上，点 B 在反比例函数 y＝ （k ≠0）的第一象限内的图象上，OA＝3，OC＝5，动点 P 在 x 轴的上方，且满足 S△PAO＝ S 矩形 OABC． （1）若点 P 在这个反比例函数的图象上，求点 P 的坐标； （2）连接 PO、PA，求 PO+PA 的最小值； （3）若点 Q 是平面内一点，使得以 A、B、P、Q 为顶点的四边形是菱形，则请你直接写 出满足条件的所有点 Q 的坐标． 解：（1）由题意，可知：点 B 的坐标为（3，5）． ∵点 B 在反比例函数 y＝ （k≠0）的第一象限内的图象上， ∴k＝3×5＝15， ∴反比例函数的解析式为 y＝ ． ∵S△PAO＝ S 矩形 OABC， ∴ ×3×yP＝ ×3×5， ∴yP＝3． 当 y＝3 时， ＝3，解得：x＝5， ∴当点 P 在这个反比例函数的图象上时，点 P 的坐标为（5，3）． （2）由（1）可知：点 P 在直线 y＝3 上，作点 O 关于直线 y＝3 的对称点 O′，连接 AO ′交直线 y＝3 于点 P，此时 PO+PA 取得最小值，如图 1 所示． ∵点 O 的坐标为（0，0）， ∴点 O′的坐标为（0，6）． ∵点 A 的坐标为（3，0）， ∴AO′＝ ＝3 ， ∴PO+PA 的最小值为 3 ． （3）∵AB∥y 轴，AB＝5，点 P 的纵坐标为 3， ∴AB 不能为对角线，只能为边． 设点 P 的坐标为（m，3）， 分两种情况考虑，如图 2 所示： ①当点 Q 在点 P 的上方时，AP＝AB＝5，即（m﹣3）2+（3﹣0）2＝25， 解得：m1＝﹣1，m2＝7， ∴点 P1 的坐标为（﹣1，3），点 P2 的坐标为（7，3）． 又∵PQ＝5，且 PQ∥AB∥y 轴， ∴点 Q1 的坐标为（﹣1，8），点 Q2 的坐标为（7，8）； ②当点 Q 在点 P 的下方时，BP＝AB＝5，即（m﹣3）2+（3﹣5）2＝25， 解得：m3＝3﹣ ，m4＝3+ ， 同理，可得出：点 Q3 的坐标为（3﹣ ，﹣2），点 Q4 的坐标为（3+ ，﹣2）． 综上所述：当以 A、B、P、Q 为顶点的四边形是菱形时，点 Q 的坐标为（﹣1，8），（7，8）， （3﹣ ，﹣2）或（3+ ，﹣2）． 11．如图，已知 C，D 是反比例函数 y＝ 图象在第一象限内的分支上的两点，直线 CD 分别 交 x 轴、y 轴于 A，B 两点，设 C，D 的坐标分别是（x1，y1）、（x2，y2），且 x1＜x2，连接 OC、OD． （1）若 x1+y1＝x2+y2，求证：OC＝OD； （2）tan∠BOC＝ ，OC＝ ，求点 C 的坐标； （3）在（2）的条件下，若∠BOC＝∠AOD，求直线 CD 的解析式． （1）证明：∵C，D 是反比例函数 y＝ 图象在第一象限内的分支上的两点， ∴y1＝ ，y2＝ ． ∵x1+y1＝x2+y2，即 x1+ ＝x2+ ， ∴x1﹣x2＝ ． 又∵x1＜x2， ∴ ＝1， ∴ ＝x2＝y1， ＝x1＝y2． ∴OC＝ ＝ ，OD＝ ＝ ， ∴OC＝OD． （2）解：∵tan∠BOC＝ ， ∴ ＝ ． 又∵OC＝ ， ∴ + ＝10， ∴x1＝1，y1＝3 或 x1＝﹣1，y1＝﹣3． ∵点 C 在第一象限， ∴点 C 的坐标为（1，3）． （3）解：∵∠BOC＝∠AOD， ∴tan∠AOD＝ ， ∴ ＝ ． ∵点 C（1，3）在反比例函数 y＝ 的图象上， ∴m＝1×3＝3， ∴x2•y2＝3， ∴x2＝3，y2＝1 或 x2＝﹣3，y2＝﹣1． ∵点 D 在第一象限， ∴点 D 的坐标为（3，1）． 设直线 CD 的解析式为 y＝kx+b（k≠0）， 将 C（1，3），D（3，1）代入 y＝kx+b，得： ， 解得： ， ∴直线 CD 的解析式为 y＝﹣x+4． 12．如图，在平面直角坐标系中，矩形 OABC 的两边分别在 x 轴、y 轴上，D 是对角线的交点， 若反比例函数 y＝ 的图象经过点 D，且与矩形 OABC 的两边 AB，BC 分别交于点 E，F． （1）若 D 的坐标为（4，2） ①则 OA 的长是 8 ，AB 的长是 4 ； ②请判断 EF 是否与 AC 平行，井说明理由； ③在 x 轴上是否存在一点 P．使 PD+PE 的值最小，若存在，请求出点 P 的坐标及此时 PD+PE 的长；若不存在．请说明理由． （2）若点 D 的坐标为（m，n），且 m＞0，n＞0，求 的值． 解：（1）①∵点 D 的坐标为（4，2）， ∴点 B 的坐标为（8，4）， ∴OA＝8，AB＝4． 故答案为：8；4． ②EF∥AC，理由如下： ∵反比例函数 y＝ 的图象经过点 D（4，2）， ∴k＝4×2＝8． ∵点 B 的坐标为（8，4），BC∥x 轴，AB∥y 轴， ∴点 F 的坐标为（2，4），点 E 的坐标为（8，1）， ∴BF＝6，BE＝3， ∴ ＝ ， ＝ ， ∴ ＝ ． ∵∠ABC＝∠EBF， ∴△ABC∽△EBF， ∴∠BCA＝∠BFE， ∴EF∥AC． ③作点 E 关于 x 轴对称的点 E′，连接 DE′交 x 轴于点 P，此时 PD+PE 的值最小，如图所 示． ∵点 E 的坐标为（8，1）， ∴点 E′的坐标为（8，﹣1）， ∴DE′＝ ＝5． 设直线 DE′的解析式为 y＝ax+b（a≠0）， 将 D（4，2），E′（8，﹣1）代入 y＝ax+b，得： ， 解得： ， ∴直线 DE′的解析式为 y＝﹣ x+5． 当 y＝0 时，﹣ x+5＝0， 解得：x＝ ， ∴当点 P 的坐标为（ ，0）时，PD+PE 的值最小，最小值为 5． （2）∵点 D 的坐标为（m，n）， ∴点 B 的坐标为（2m，2n）． ∵反比例函数 y＝ 的图象经过点 D（m，n）， ∴k＝mn， ∴点 F 的坐标为（ m，2n），点 E 的坐标为（2m， n）， ∴BF＝ m，BE＝ n， ∴ ＝ ， ＝ ， ∴ ＝ ． 又∵∠ABC＝∠EBF， ∴△ABC∽△EBF， ∴ ＝ ＝ ． 13．如图，一次函数 y＝kx+b（k≠0）的图象与反比例函数 y＝ （m≠0）的图象交于 A（﹣ 3，1），B（1，n）两点． （1）求反比例函数和一次函数解析式； （2）结合图象直接写出不等式 ﹣kx﹣b＞0 的解． 解：（1）∵点 A（﹣3，1）在反比例函数 y＝ （m≠0）的图象上， ∴m＝（﹣3）×1＝﹣3， ∴反比例函数的表达式为 y＝﹣ ， ∵点 B（1，n）也在反比例函数 y＝﹣ 的图象上， ∴n＝﹣ ＝﹣3，即 B（1，﹣3）， 把点 A（﹣3，1），点 B（1，﹣3）代入一次函数 y＝kx+b 中， 得 ， 解得 ， ∴一次函数的表达式为 y＝﹣x﹣2； （2）如图所示，当 ＞kx+b 时，x 的取值范围是﹣3＜x＜0 或 x＞1， 所以不等式 ﹣kx﹣b＞0 的解是：﹣3＜x＜0 或 x＞1． 14．如图，在 平面直角坐标系 xOy 内，函数 y＝ 的图象与反比例函数 y＝ （k≠0）图 象有公共点 A，点 A 的坐标为（8，a），AB⊥x 轴，垂足为点 B． （1）求反比例函数的解析式； （2）点 P 在线段 OB 上，若 AP＝BP+2，求线段 OP 的长；（3）点 D 为射线 OA 上一点，在 （2）的条件下，若 S△ODP＝S△ABO，求点 D 的坐标． 解：（1）∵函数 y＝ 的图象过点 A（8，a）， ∴a＝ ×8＝4， ∴点 A 的坐标为（8，4）， ∵反比例函数 y＝ （k≠0）图象过点 A（8，4）， ∴4＝ ，得 k＝32， ∴反比例函数的解析式为 y＝ ； （2）设 BP＝b，则 AP＝b+2， ∵点 A（8，4），AB⊥x 轴于点 B， ∴AB＝4，∠ABP＝90°， ∴b2+42＝（b+2）2， 解得，b＝3， ∴OP＝8﹣3＝5， 即线段 OP 的长是 5； （3）设点 D 的坐标为（d， d）， ∵点 A（8，4），点 B（8，0），点 P（5，0），S△ODP＝S△ABO， ∴ ， 解得，d＝ ， ∴ d＝ ， ∴点 D 的坐标为（ ， ）． 15．阅读理解： 如图（1），在平面直角坐标系 xOy 中，已知点 A 的坐标是（1，2），点 B 的坐标是（3，4）， 过点 A、点 B 作平行于 x 轴、y 轴的直线相交于点 C，得到 Rt△ABC，由勾股定理可得， 线段 AB＝ ＝ ． 得出结论： （1）若 A 点的坐标为（x1，y1），B 点的坐标为（x2，y2）请你直接用 A、B 两点的坐标表 示 A、B 两点间的距离； 应用结论： （2）若点 P 在 y 轴上运动，试求当 PA＝PB 时，点 P 的坐标． （3）如图（2）若双曲线 L1：y＝ （x＞0）经过 A（1，2）点，将线段 OA 绕点 O 旋转， 使点 A 恰好落在双曲线 L2：y＝﹣ （x＞0）上的点 D 处，试求 A、D 两点间的距离． 解：（1）∵A 点的坐标为（x1，y1），B 点的坐标为（x2，y2）， ∴根据两点间的距离公式得，AB＝ ； （2）设点 P（0，a）， ∵A 的坐标是（1，2），点 B 的坐标是（3，4）， ∵PA＝ ，PB＝ ， ∵PA＝PB， ∴ ＝ ， ∴a＝5， ∴P（0，5）； （3）∵双曲线 L1：y＝ （x＞0）经过 A（1，2）点， ∴OA＝ ，k＝1×2＝2， ∴双曲线 L1：y＝ （x＞0），双曲线 L2：y＝﹣ （x＞0）， 设点 D 坐标为（m，﹣ ）（m＞0）， ∴OD＝ ， 由旋转知，OA＝OD， ∴ ＝ ， ∴m＝±1 或 m＝±2， ∵m＞0， ∴m＝1 或 m＝2， ∴D（1，﹣2）或（2，﹣1）． ∵A（1，2）， ∴AD＝4 或 ．