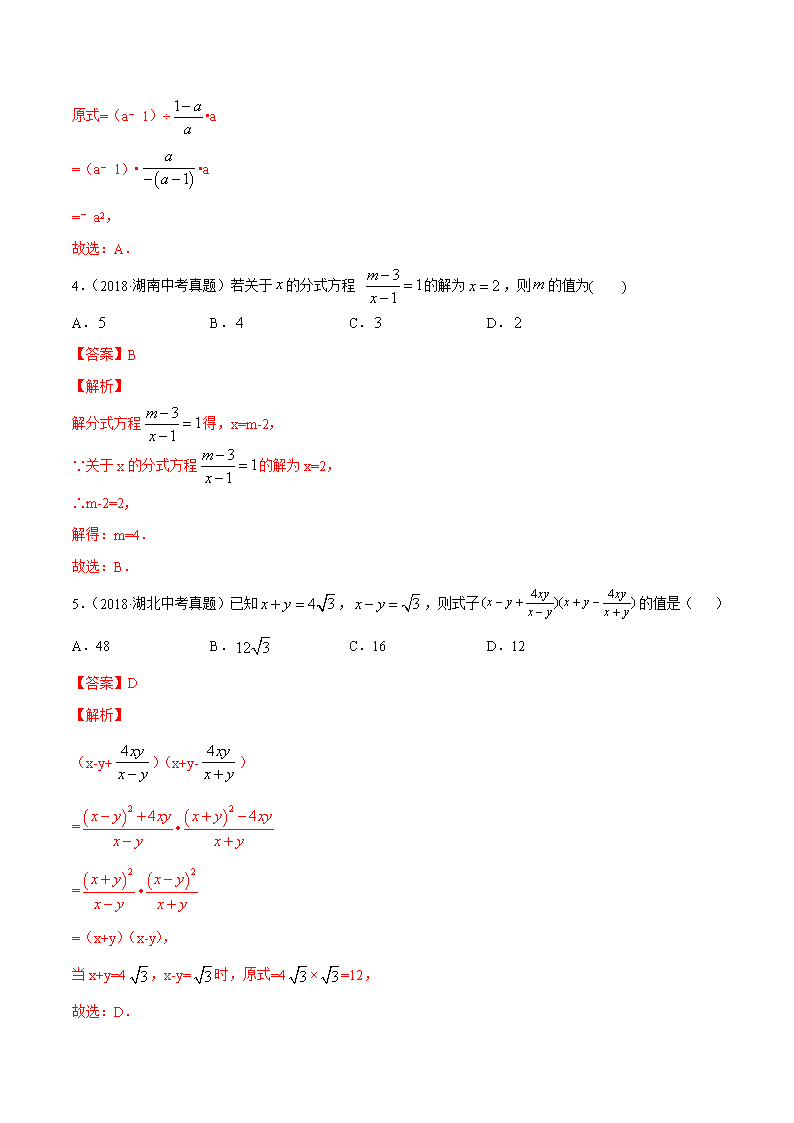【精品试卷】中考数学一轮复习 专题测试09 分式与分式方程（培优提高）（教师版） 9页

专题 09 分式与分式方程（专题测试-提高） 学校:___________姓名：___________班级：___________考号：___________ 一、选择题（共 12 小题，每小题 4 分，共 48 分） 1．（2019·浙江中考模拟）下列运算正确的是（ ） A．a2+a3=a5 B．a（b﹣1）=ab﹣a C．3a﹣1= 1 3a D．（3a2﹣6a+3）÷3=a2﹣2a 【答案】B 【详解】 解：A、a2、a3 不是同类项，不能合并，错误； B、a（b﹣1）=ab﹣a，正确； C、3a﹣1= 3 a ，错误； D、（3a2﹣6a+3）÷3=a2﹣2a+1，错误； 故选：B． 2．（2019·天津二十中中考模拟）已知 1 1 1 2a b   ，则 ab a b 的值是（ ） A． 1 2 B．－ 1 2 C．2 D．－2 【答案】D 【解析】 解：∵ ， ∴ a ab - = ， ∴ = ， ∴ =-2． 故选 D． 3．（2018·山东中考真题）化简（a﹣1）÷（ 1 a ﹣1）•a 的结果是（ ） A．﹣a2 B．1 C．a2 D．﹣1 【答案】A 【解析】 原式=（a﹣1）÷1 a a  •a =（a﹣1）•  1 a a  •a =﹣a2， 故选：A． 4．（2018·湖南中考真题）若关于 x 的分式方程 3 11 m x   的解为 2x  ，则 m 的值为( ) A．5 B． 4 C．3 D． 2 【答案】B 【解析】 解分式方程 3 11 m x   得，x=m-2， ∵关于 x 的分式方程 3 11 m x   的解为 x=2， ∴m-2=2， 解得：m=4． 故选：B． 5．（2018·湖北中考真题）已知 4 3x y  ， 3x y  ，则式子 4 4( )( )xy xyx y x yx y x y      的值是（ ） A．48 B．12 3 C．16 D．12 【答案】D 【解析】 （x-y+ 4xy x y ）（x+y- 4xy x y ） =    2 24 4•x y xy x y xy x y x y       =    2 2 •x y x y x y x y     =（x+y）（x-y）， 当 x+y=4 3 ，x-y= 3 时，原式=4 3 × 3 =12， 故选：D． 6．（2019·黑龙江中考模拟）分式方程 1 1 12 x x x    的解是（ ） A． 1x  B． 1x   C． 3x  D． 3x   【答案】A 【解析】 1 1 12 x x x    ， 去分母，方程两边同时乘以 x（x-2）得： （x+1）（x-2）+x=x（x-2）， x2-x-2+x=x2-2x， x=1， 经检验，x=1 是原分式方程的解， 故选 A． 7．（2018·山西中考模拟）化简 2 2 1 1 2 1 a a a a a    的结果是（ ） A． 1 2 B． 1 a a  C． 1a a  D． 1 2 a a   【答案】B 【解析】 原式=     2 1 1 11 a a a aa     = 1 a a  ． 故选 B． 8．（2019·河南中考模拟）衡阳市某生态示范园计划种植一批梨树，原计划总产值 30 万千克，为了满足市场 需求，现决定改良梨树品种，改良后平均每亩产量是原来的 1.5 倍，总产量比原计划增加了 6 万千克，种植 亩数减少了 10 亩，则原来平均每亩产量是多少万千克？设原来平均每亩产量为 x 万千克，根据题意，列方 程为 ( ) A． 30 36 101.5x x   B． 30 30 101.5x x   C． 36 30 101.5x x   D． 30 36 101.5x x   【答案】A 【详解】 设原计划每亩平均产量 x 万千克，则改良后平均每亩产量为1.5x 万千克， 根据题意列方程为： 30 36 101.5x x   ． 故选： A ． 9．（2019·山东中考模拟）关于 x 的分式方程 2 3 0x x a   解为 4x  ，则常数 a 的值为( ) A． 1a  B． 2a  C． 4a  D． 10a  【答案】D 【解析】 把 x=4 代入方程 2 3 0x x a   ，得 2 3 04 4 a   ， 解得 a=10． 故选：D． 10．（2018·江苏中考模拟）已知空气的单位体积质量是 0.001239g/cm3，则用科学记数法表示该数为（ ） A．1.239×10﹣3g/cm3 B．1.239×10﹣2g/cm3 C．0.1239×10﹣2g/cm3 D．12.39×10﹣4g/cm3 【答案】A 【解析】 试题分析：0.001239=1.239×10﹣3．故选 A． 11．（2019·北京中考真题）如果 1m n  ，那么代数式  2 2 2 2 1m n m nm mn m       的值为（ ） A．-3 B．-1 C．1 D．3 【答案】D 【详解】 解：原式=  2 2 2 2 1m n m nm mn m       2 ( )( )( ) ( ) m n m n m n m nm m n m m n           3 ( )( ) 3( )( ) m m n m n m nm m n       1m n  ∴原式=3，故选 D. 12．（2019·浙江中考模拟）式子 2x 1 x 1   有意义的 x 的取值范围是（ ） A． 1x 2   且 x≠1 B．x≠1 C． 1x 2   D． 1x> 2  且 x≠1 【答案】A 【解析】 根据二次根式被开方数必须是非负数和分式分母不为 0 的条件，要使 2x 1 x 1   在实数范围内有意义，必须 12x 1 0 x 1{ { x2x 1 0 2x 1          且 x 1 。故选 A。 二、填空题（共 5 小题，每小题 4 分，共 20 分） 13．（2018·四川中考模拟）若 a2 3a 1 b2 2b 1 ，则a2 1 a2 b 。 【答案】6 【解析】 ∵ a2 3a 1 b2 2b 1 a2 3a 1 b 1 ， ∴ a2 3a 1 b 1 a 3 1 a b o a 1 a 3 b o a 1 a 9 b o a 1 a 7 b o 。 ∴a2 1 a2 b 䁩 1 䁩 o 。 14．（2018·广西中考模拟）当 x 取_____时，分式 1 11 1 x x x   有意义． 【答案】x≠0 且 x≠±1 【解析】 由题意可知，只有当： 0 1 0 11 01 x x x x x x             时，原分式才有意义，解得： 0 1 1 x x x        ，即当 x≠0 且 x≠±1 时，原分式 有意义． 故答案为：x≠0 且 x≠±1． 15．（2018·内蒙古中考真题）化简 3 m m  + 2 6 9m  ÷ 2 3m 的结果是___________________. 【答案】1 【详解】 m m 3 + 2 6 m 9 ÷ 2 m 3 =    6 3·3 3 3 2 m m m m m    = 3 3 3 m m m   =1， 故答案为：1. 16．（2018·山东省潍坊第八中学中考真题）当 m  ____________时,解分式方程 5 3 3 x m x x    会出现增根． 【答案】2 【解析】 分式方程可化为：x-5=-m， 由分母可知，分式方程的增根是 3， 当 x=3 时，3-5=-m，解得 m=2， 故答案为：2． 17．（2019·湖北中考模拟）若关于 x 的分式方程 3 3 3 x a x x   =2a 无解，则 a 的值为_____． 【答案】1 或 1 2 【解析】 去分母得： x-3a=2a（x-3）， 整理得：（1-2a）x=-3a， 当 1-2a=0 时，方程无解，故 a= 1 2 ； 当 1-2a≠0 时，x= 3 1 2 a a   =3 时，分式方程无解， 则 a=1， 故关于 x 的分式方程 3 3 3 x a x x   =2a 无解，则 a 的值为：1 或 1 2 ． 故答案为：1 或 1 2 ． 三、解答题（共 4 小题，每小题 8 分，共 32 分） 18．（2018·湖南中考模拟）计算题 （1）先化简，再求值： 2 1 x x  ÷（1+ 2 1 1x  ），其中 x=2017． （2）已知方程 x2﹣2x+m﹣3=0 有两个相等的实数根，求 m 的值． 【答案】（1）2018；（2）m=4 【解析】 （1） 2 1 x x  ÷（1+ 2 1 1x  ） = 2 2 2 1 1 1 1 x x x x    =   2 2 1 1 1 x xx x x   =x+1， 当 x=2017 时，原式=2017+1=2018 （2）解：∵方程 x2﹣2x+m﹣3=0 有两个相等的实数根， ∴△=（﹣2）2﹣4×1×（m﹣3）=0， 解得，m=4 19．（2019·山东中考模拟）某超市预测某饮料有发展前途，用 1600 元购进一批饮料，面市后果然供不应求， 又用 6000 元购进这批饮料，第二批饮料的数量是第一批的 3 倍，但单价比第一批贵 2 元. (1)第一批饮料进货单价多少元？ (2)若二次购进饮料按同一价格销售，两批全部售完后，获利不少于 1200 元，那么销售单价至少为多少元？ 【答案】（1）第一批饮料进货单价为 8 元.(2) 销售单价至少为 11 元. 【详解】（1）设第一批饮料进货单价为 x 元，则： 1600 60003 2x x    解得： 8x  经检验： 8x  是分式方程的解 答：第一批饮料进货单价为 8 元. （2）设销售单价为 m 元，则：    8 200 10 600 1200m m      ， 化简得：    2 8 6 10 12m m    ， 解得： 11m  ， 答：销售单价至少为 11 元. 20．（2019·山东中考模拟）先化简，再求值（ o 䁕 ﹣ 䁕 䁕 ）÷ 䁕 䁕 + 䁕 ，其中 a，b 满足 a+b﹣ o =0． 【答案】原式= o 䁕 =2 【详解】 （ o 䁕 ﹣ 䁕 䁕 ）÷ 䁕 䁕 + 䁕 = 䁕䁕 䁕 䁕 䁕 䁕 = o 䁕 由 a+b﹣ o =0，得到 a+b= o ， 则原式= oo =2． 21．（2018·贵州中考真题）先化简，再求值： 2 2 8 24 4 2 x xx x x         ，其中 2x  . 【答案】 2 2x  ， 1 2  . 【解析】 原式     2 2 2 28 2 22 x xx x xx            2 2 2 8 4 22 x x xx      2 8 2 42 x x    = 2 2x  . ∵ 2x  ，∴ 2x   ，舍去 2x  ， 当 2x   时，原式 2 1 2 2 2     .