九年级数学上册第六章反比例函数2反比例函数的图象与性质第2课时反比例函数的性质教学课件新版北师大版 27页

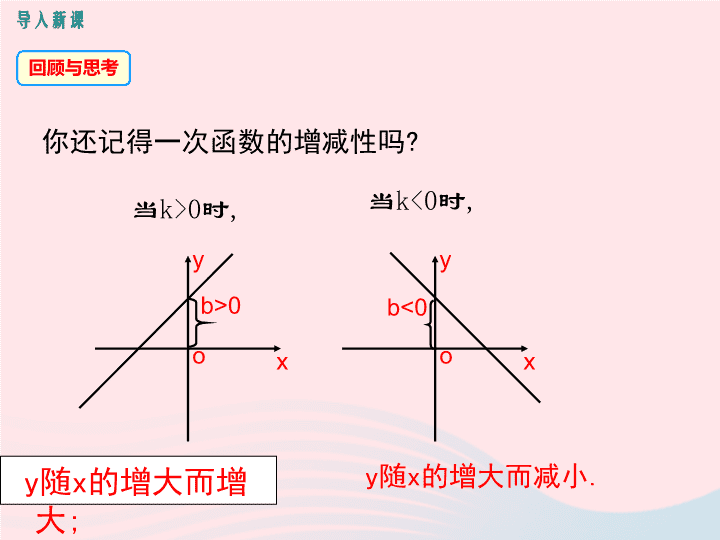
6.2 反比例函数的图象与性质 第六章 反比例函数 第 2 课时　反比例函数的性质 导入新课 讲授新课 当堂练习 课堂小结 学习目标 1. 理解并掌握反比例函数图象的性质 ; （重点） 2. 能利用反比例函数的图象与性质解决问题 . （难点） y 随 x 的增大而增大 ; 你还记得一次函数的增减性吗 ? x y o x y o y 随 x 的增大而减小 . b>0 b<0 当 k>0 时 , 当 k<0 时 , 导入新课 回顾与思考 x y o 3 4 5 -1 -3 -4 -1 -2 -4 -5 y= -3 2 1 -1 -2 1 2 3 4 5 x 6 观察反比例函数图象的增减性 . x y o 3 4 5 -1 -3 -4 -1 -2 -4 -5 y= -3 2 1 -1 -2 -5 1 2 3 4 5 x 6 0 1 2 3 4 5 6 7 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 -6 -1 -2 -3 -4 -5 -6 -7 y=- 6 x y x 问题： 观察下列的函数图象，填一填 . y y y x x x O O O 反比例函数的性质 一 (2) 函数图象分别位于哪几个象限？ 第二、四象限内 (1) 上面三个函数相应的 k 值分别是 ________ ，则 k___0. -2,-4,-6 ＜ x ＜ 0 时，图象在第二象限； x ＞ 0 时，图象在第四象限． (4) 在每一象限内 , 曲线从左往右 ______, 所以随着 x 值的增大， y 的值怎样变化？ 逐渐上升，减小． (3) 当 x 取什么值时，图象在第二象限？当 x 取什么值时，图象在第四象限？ y x y 0 反比例函数的增减性 当 k>0 时，在每一个象限内， y 随 x 的增大而减小。 当 k>0 时，在每一支曲线上， y 随 x 的增大而减小。 x y 0 归纳总结 1. 函数 的图象，在每一象限内 y 随 x 的增大而 _ _____ . y = x 5 2. 在双曲线 的一支上， y 随 x 的增大而减小，则 m 的取值范围是 ____ . m -2 x y = m > 2 增大 练一练 典例精析 例 1 ： 已知反比例函数 的图象过点 (-2 ， -3) ， 函数图象上有两点 A ( ), B (5, y 2 ) , C (-8, y 3 ) , 则 y 1 与 y 2 、 y 3 的大小关系为 ( ) A. y 1 > y 2 > y 3 B. y 1 < y 2 < y 3 C. y 2 > y 1 > y 3 D. 不能确定 C 解析： 已知反比例函数过点（ -2 ， -3 ），所以可知 k > 0 , 可判断 y 1 >0 ， y 2 > 0 ， y 3 ＜ 0 . 由概念可知 , 当 k >0 时，在每个象限内， y 随 x 的增大而减小，所以 y 2 > y 1 >0> y 3 . 已知两点（ ， ），（ ， ）在函数 的图象上，当 ＞ ＞ 0 时，下列结论正确的是 （ 　） 　 A. ＞ ＞ 0 B. ＜ ＜ 0 C. ＞ ＞ 0 D. ＜ ＜ 0 Ｄ 变式拓展 反比例函数解析式中 k 的几何意义 二 合作探究 1. 在反比例函数 的图象上分别取点 P ， Q 向 x 轴、 y 轴作垂线，围成面积 分别 为 S 1 ， S 2 的矩形，填写表格： 4 4 S 1 =S 2 S 1 =S 2 =k S 1 的值 S 2 的值 S 1 与 S 2 的 关系 猜想与 k 的关系 P （ 2,2 ） Q （ 4,1 ） 1 2 3 4 5 -1 -3 -2 -4 -5 1 2 3 4 -1 -2 -3 -4 -5 5 x y O Q P S 1 S 2 2. 若在反比例函数 中也用同样的方法分别取 P ， Q 两点，填写表格： S 1 的值 S 2 的值 S 1 与 S 2 的关系 猜想与 k 的关系 P （ -1,4 ） Q （ -2,2 ） 4 4 S 1 =S 2 S 1 =S 2 =-k y x o P Q S 1 S 2 由前面的探究过程，可以猜想 : 若点 P 是 图象上的任意一点 ，作 P A 垂直于 x 轴，作 P B 垂直于 y 轴，矩形 AOB P 的面积与 k 的关系是 S 矩形 AOB P = |k| . 合理猜想 y x O P S 我们就 k<0 的情况给出证明： 设点 P 的坐标为 ( a , b ) A B ∵ 点 P ( a , b ) 在函数 的图象上， ∴ ，即 ab=k ∴ S 矩形 AOB P = PB · PA=-a · b=-ab=-k ； 若点 P 在第二象限，则 a <0 ， b >0 若点 P 在第四象限，则 a >0 ， b <0 ∴ S 矩形 AOB P = PB · PA=a · （ -b ） =-ab=-k . B P A 综上， S 矩形 AOB P = |k|. 自己尝试证明 k>0 的情况 . 方法归纳 点 Q 是其图象上的任意一点 ，作 QA 垂直于 y 轴，作 QB 垂直于 x 轴，矩形 AOBQ 的面积与 k 的关系是 S 矩形 AOBQ = 推理： △ QAO 与 △ QBO 的面积和 k 的关系是 S △ QAO =S △ QBO = Q 对于反比例函数 ， A B |k| 反比例函数的 面积不变性 y x O 典例精析 例 3. 如图，在函数 的图像上有三点 A 、 B 、 C ，过这三点分别向 x 轴、 y 轴作垂线，过每一点所作的两条垂线与 x 轴、 y 轴围成的矩形的面积分别为 S A ， S B ， S C ， 则（ ） y x O A.S A >S B >S C B.S A - 4 当堂练习 4. 下列关于反比例函数 的三个结论： (1) 它的图象经过点 （ -1,12 ） 和点 （ 10 ， -1.4 ）； (2) 它的图象在每一个象限内， y 随 x 的增大而减小； (3) 它的图象在二、四象限内 . 其中正确的是 （填序号）． (1)(3) 5. 如果点（a,-2a）在双曲线上，那么在第几象限内，y随x的增大而__________ 增大 6. 如图所示，反比例函数 （ k≠0 ）的图象上有一点 A , AB ∥ x 轴交 y 轴于点 B ，△ ABO 的面积是 1 ，则反比例函数的表达式是（ ） A. B. C. D. y x O A B C 7 . 已知 k<0, 则函数 y 1 =kx,y 2 = 在同一坐标系中的图象大致是 ( ) x y 0 x y 0 x y 0 x y 0 (A) (B) (C) (D) D x k 拓展训练 y x O A． y x O B． y x O C． y x O D． 8 . 若点 在函数 （x＜0）的图象上， ，则它的图象大致是（ ） B 9. 已知反比例函数的图象的一支如图所示． (1) 判断 k 是正数还是负数； (2) 求这个反比例函数的表达式； (3) 补画这个反比例函数图象的另一支． 解： (1) 因为反比例函数的图象在第二象限，所以 k 是负数． (2) 设反比例函数的表达式为 将 (-4 ， 2) 代入其中，解得 k=- 8 ，所以反比例函数的表达式为 : (3) 根据反比例函数图象的中心对称性可补画出另一支，图象略． 课堂小结 反比例函数的性质 性质 反比例函数图象中比例系数 k 的几何意义 当 k ＞ 0 时，在每一象限内， y 的值随 x 的增大而减小 . 当 k <0 时，在每一象限内， y 的值随 x 的增大而增大 .