反比例函数的应用学案 3页

‎6.3 反比例函数的应用 ‎ 一、知识要点 ‎1、在实际问题中构建函数的数学模型,通过实际问题提高学生的分析问题解决问题的能力。‎ ‎2、学生能根据实际问题列出反比例函数的解析式，根据自变量求因变量，根据因变量求自变量。3、结合图形求自变量、因变量。进一步体会反比例函数的图象是中心对称图形，加强学生的数形结合的能力。‎ ‎4、课前预习：‎ ①反比例函数的定义、图象、性质分别是什么？ ‎ ②反比例函数的图象既是______对称图形，又是 ______对称图形 二、典型例题分析：‎ 例1、某科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全迅速通过这片湿地,他们沿着前进路线铺垫了若干木板,构筑了一条临时通道,从而顺利完成了任务.你能解释他们这样做的道理吗?当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强P(Pa)将如何变 如果人和木板对湿地地面的压力合计600N,那么 (1)用含S的代数式表示P,P是S的反比例函数吗?为什么?‎ ‎(2)当木板面积为0.2m2时,压强是多少?‎ ‎(3)如果要求压强不超过6000Pa,木板面积至少要多大?‎ ‎(4)在直角坐标系,作出相应函数的图象(作在课本143页的图上)‎ 分析：本题为和物理知识相连系的实际应用，可先回顾压力、压强、面积三者之间的关系，然后分析谁是常量，谁是变量。⑴中表示P应为P= ‎ ⑵中根据自变量求因变量， ‎ ‎ ⑶中根据因变量求自变量。或用不等式来求解。⑷注意和实际问题的联系。‎ ‎ 解：‎ 跟踪练习：‎ ‎1、蓄电池的电压为定值，使用此电源时，电流I（A）与电阻R（‎ ‎ ）之间的函数关系如图5-8所示：探究（1）蓄电池的电压是多少？你能写出这一函数的表达式吗？‎ ‎（2）完成下表：并回答问题，如果以此蓄电池为电源的用电器限制电流不得超过10A，那么用电器的可变电阻应控制在什么范围内？‎ R/‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ I/A ‎ ‎ 三、基础练习 ‎2、甲乙两地相距100km，一辆汽车从甲地开往乙地，把汽车到达乙地所用的时间y(h)‎ 3‎ 表示为汽车的平均速度x(km/h)的函数，则这个函数的图象大致是（ ）‎ ‎3.某蓄水池的排水管每时排水8m3,6h可将满池水全部排空.‎ ‎(1)蓄水池的容积是多少?‎ ‎(2)如果增加排水管,使每时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化?‎ ‎(3)写出t与Q之间的函数关系式;‎ ‎(4)如果准备在5h内将满池水排空,那么每时的排水量至少为多少?‎ ‎(5)已知排水管的最大排水量为每时12m3/h,那么最少多长时间可将满池水全部排空?‎ ‎(6)画出函数图象,根据图象请对问题(4)和(5)作出直观解释,并和同伴交流.‎ 四、知识延伸 例2、如图5-9，正比例函数y=k1x,和反比例函数y=K2X-1的图象相交于A，B两点，其中点A的坐标 ⑴分别写出这两个函数的表达式；‎ ⑵你能求出点B的坐标吗？你是怎样求出的？与同伴进行交流。‎ 分析：本题是正比例函数与反比例函数相结合的综合性题目，重在考察学生的数形结合的能力，⑴中只要把点的坐标代入便可求出表达式;⑵中可用代数法也可利用反比例函数的中心对称性来解决。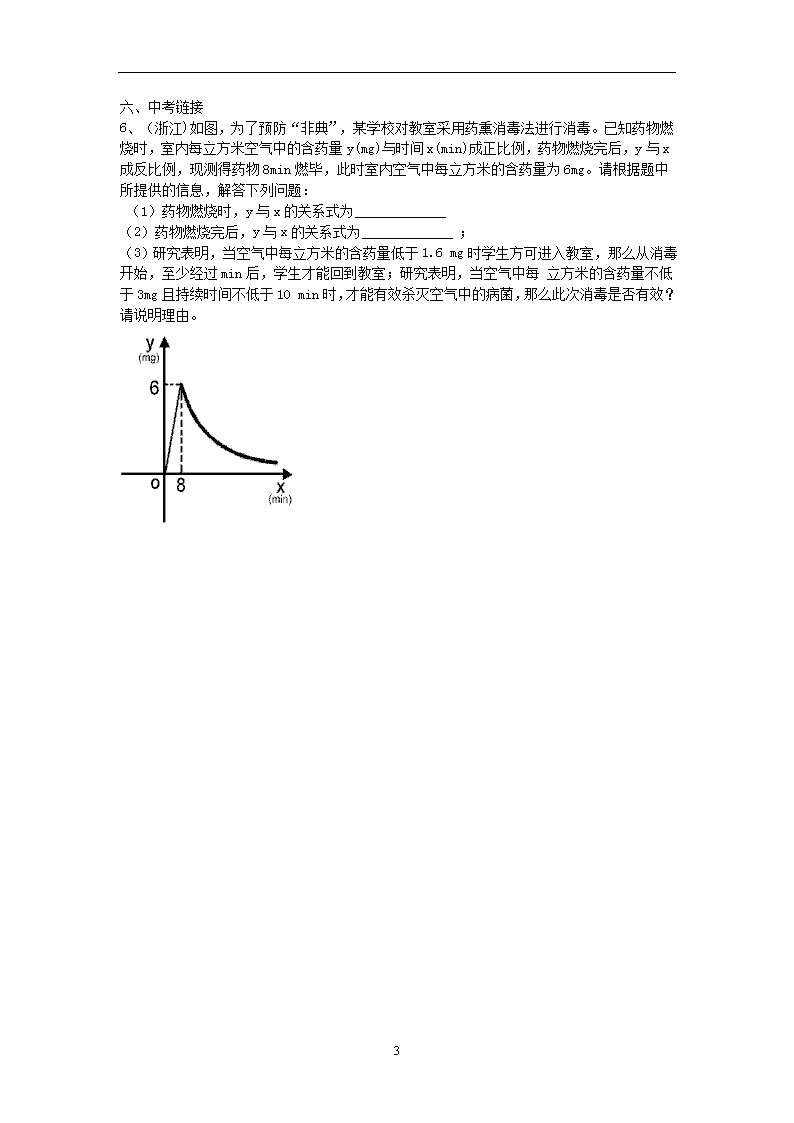‎ 解：‎ 五、拓展提高 ‎5、‎ A y O B x M N 3‎ 六、中考链接 ‎6、（浙江)如图，为了预防“非典”，某学校对教室采用药熏消毒法进行消毒。已知药物燃烧时，室内每立方米空气中的含药量y(mg)与时间x(min)成正比例，药物燃烧完后，y与x成反比例，现测得药物8min燃毕，此时室内空气中每立方米的含药量为6mg。请根据题中所提供的信息，解答下列问题：‎ ‎ （1）药物燃烧时，y与x的关系式为 ‎ ‎（2）药物燃烧完后，y与x的关系式为 ； ‎ ‎（3）研究表明，当空气中每立方米的含药量低于1.6 mg时学生方可进入教室，那么从消毒开始，至少经过min后，学生才能回到教室；研究表明，当空气中每 立方米的含药量不低于3mg且持续时间不低于10 min时，才能有效杀灭空气中的病菌，那么此次消毒是否有效？请说明理由。 ‎ ‎ ‎ 3‎