2019年湖南郴州中考数学试题（解析版） 15页

‎{来源}2019 年郴州市初中学业水平考试数学试卷 ‎{适用范围:3． 九年级}‎ ‎{标题}2019年湖南省郴州市中考数学试卷 考试时间：120分钟 满分：130分 ‎{题型:1－选择题}一、选择题：本大题共8小题，每小题8分，合计24分． ‎ ‎{题目}1．（2019年郴州T1）如右图，数轴上表示－2 的相反数的点是 A．M ‎ B．N C．P ‎ D．Q ‎{答案}A ‎{解析}本题考查了有理数与数轴间的关系，由于点M对应的有理数是－2，因此本题选A．‎ ‎{分值}3‎ ‎{章节:[1－1－2－2]数轴}‎ ‎{考点:数轴表示数}‎ ‎{类别:常考题}‎ ‎{难度:1－最简单}‎ ‎{题目}2．（2019年郴州T2）如图是我国几家银行的标志，其中既是轴对称图形又是中心对称图形的是 ‎ ‎ A． ‎ B． C． D．‎ ‎{答案}C ‎{解析}本题考查了轴对称图形；中心对称图形，根据轴对称图形与中心对称图形的概念进行判断即可解答本题．中国建设银行标志：不是轴对称图形，也不是中心对称图形，不符合题意；中国农业银行标志：是轴对称图形，不是中心对称图形，不符合题意；中国银行标志：既是轴对称图形又是中心对称图形，符合题意；中国人民银行标志：是轴对称图形，不是中心对称图形，不符合题意；因此本题选C．‎ ‎{分值}3‎ ‎{章节:[1－23－2－2]中心对称图形}‎ ‎{考点:轴对称图形}‎ ‎{考点:中心对称图形}‎ ‎{类别:常考题}‎ ‎{难度:1－最简单}‎ ‎{题目}3．（2019年郴州T3）邓小平曾说：“中东有石油，中国有稀土”．稀土是加工制造国防、军工等工业品不可 或缺的原料．据有关统计数据表明：至 2017 年止，我国已探明稀土储量约 4400 万吨，居世界第一位，请用科学记数法表示 44 000 000 为 A．44×106 B． 4.4×107 C． 4.4×108 D． 0.44×109 ‎ ‎{答案}B ‎{解析}本题考查了科学计数法表示较大的数，将44 000 000用科学记数法表示为：4.4×107．因此本题选B．‎ ‎{分值}3‎ ‎{章节:[1－1－5－2]科学计数法}‎ ‎{考点:将一个绝对值较大的数科学计数法}‎ ‎{类别:常考题}‎ ‎{难度:1－最简单}‎ ‎{题目}4．（2019年郴州T）下列运算正确的是 ‎ A．(x2)3＝x5 B． C．x·x2·x4＝x6 D．＝‎ ‎{答案}D ‎{解析}本题考查了同底数幂的乘法以及二次根式的运算，利用相关运算法则进行计算，然后判断即可．(x2)3＝x6，所以A错误；，所以B错误；．x·x2·x4＝x7，所以C错误；＝，所以D正确，因此本题选D．‎ ‎{分值}3‎ ‎{章节:[1－16－3]二次根式的加减}‎ ‎{考点:同底数幂的乘法}‎ ‎{考点:幂的乘方}‎ ‎{考点:二次根式的除法法则}‎ ‎{考点:二次根式的加减法}‎ ‎{类别:常考题}‎ ‎{难度:2－简单}‎ ‎{题目}5．（2019年郴州T5）一元二次方程 2 x2 ＋ 3x − 5 ＝ 0 的根的情况为 ‎ A．有两个相等的实数根 B．有两个不相等的实数根 ‎ C．只有一个实数根 D．没有实数根 ‎{答案}B ‎{解析}本题考查了一元二次方程根的判别式，因为a＝2，b＝3，c＝－5，所以Δ＝b2－4ac＝32－4×2×(－5)＝49＞0，所以方程2 x2 ＋ 3x − 5 ＝ 0有两个不相等的实数根，因此本题选B．‎ ‎{分值}3‎ ‎{章节:[1－21－2－2]公式法}‎ ‎{考点:根的判别式}‎ ‎{类别:常考题}‎ ‎{难度:2－简单}‎ ‎{题目}6．（2019年郴州T6）下列采用的调查方式中，合适的是 ‎ A．为了解东江湖的水质情况，采用抽样调查的方式 B．我市某企业为了解所生产的产品的合格率，采用普查的方式 ‎ C．某小型企业给在职员工做工作服前进行尺寸大小的调查，采用抽样调查的方式 ‎ D．某市教育部门为了解该市中小学生的视力情况，采用普查的方式 ‎{答案}A ‎{解析}本题考查了调查方法的选择，调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来，具体问题具体分析．了解东江湖的水质情况时，若进行一次全面的调查，费大量的人力物力是得不尝失，因此宜采用抽样调查的方式，故A选项是合适的；企业为了解所生产的产品的合格率，所采取的实验多带有破坏性，因此采取抽样调查即可，故B选项不合适；小型企业员工数量有限，因此给在职员工做工作服前对每个人进行尺寸大小进行测量即可，所以C选项不合适；在了解某市中小学生的视力情况时，若进行一次全面的调查，费大量的人力物力是得不尝失的，采取抽样调查即可，故D选项不合适．因此本题选A．‎ ‎{分值}3‎ ‎{章节:[1－19－4]课题学习 选择方案}‎ ‎{考点:全面调查}‎ ‎{考点:抽样调查}‎ ‎{类别:思想方法}‎ ‎{难度:2－简单}‎ ‎{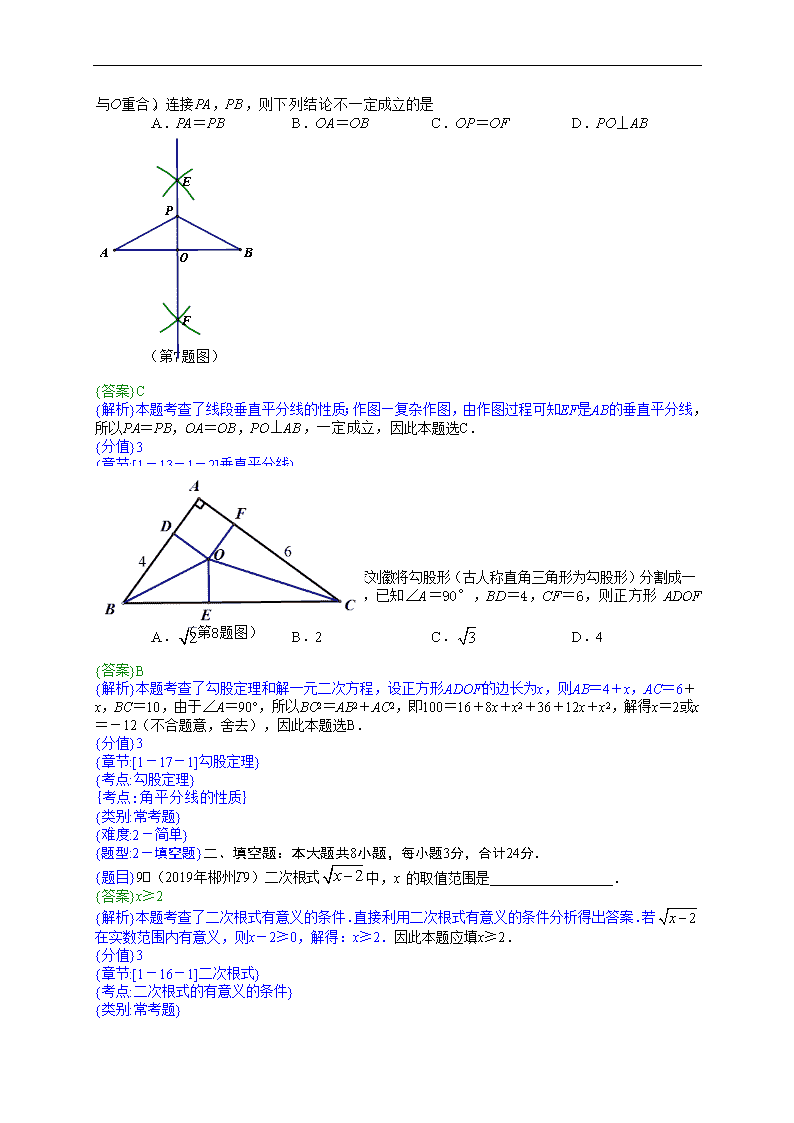题目}7．（2019年郴州T7）如图，分别以线段 AB 的两端点 A，B 为圆心，大于 AB 长为半径画弧，在线段 AB的两侧分别交于点 E，F，作直线 EF 交 AB 于点 O．在直线 EF 上任取一点 P ‎（不与 O重合），连接 PA，PB，则下列结论不一定成立的是 A．PA＝PB B．OA＝OB C．OP＝OF D．PO⊥AB ‎（第7题图）‎ ‎{答案}C ‎{解析}本题考查了线段垂直平分线的性质；作图—复杂作图，由作图过程可知EF是AB的垂直平分线，所以PA＝PB，OA＝OB，PO⊥AB，一定成立，因此本题选C．‎ ‎{分值}3‎ ‎{章节:[1－13－1－2]垂直平分线}‎ ‎{考点:垂直平分线的性质}‎ ‎{考点:与垂直平分线有关的作图}‎ ‎{考点:垂直平分线的判定}‎ ‎{类别:北京作图}‎ ‎{难度:2－简单}‎ ‎{题目}8．（2019年郴州T8）我国古代数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对 全等的三角形，如图所示，已知∠A＝90°，BD＝4，CF＝6，则正方形 ADOF 的边长是 A． B．2 C． D．4‎ ‎（第8题图）‎ ‎{答案}B ‎{解析}本题考查了勾股定理和解一元二次方程，设正方形ADOF的边长为x，则AB＝4＋x，AC＝6＋x，BC＝10，由于∠A＝90°，所以BC2＝AB2＋AC2，即100＝16＋8x＋x2＋36＋12x＋x2，解得x＝2或x＝－12（不合题意，舍去），因此本题选B．‎ ‎{分值}3‎ ‎{章节:[1－17－1]勾股定理}‎ ‎{考点:勾股定理}‎ ‎{考点:角平分线的性质}‎ ‎{类别:常考题}‎ ‎{难度:2－简单}‎ ‎{题型:2－填空题}二、填空题：本大题共8小题，每小题3分，合计24分．‎ ‎{题目}9．（2019年郴州T9）二次根式中，x 的取值范围是 ．‎ ‎{答案}x≥2‎ ‎{解析}本题考查了二次根式有意义的条件．直接利用二次根式有意义的条件分析得出答案．若在实数范围内有意义，则x－2≥0，解得：x≥2．因此本题应填x≥2．‎ ‎{分值}3‎ ‎{章节:[1－16－1]二次根式}‎ ‎{考点:二次根式的有意义的条件}‎ ‎{类别:常考题}‎ ‎{难度:2－简单}‎ ‎{题目}10．（2019年郴州T10）若，则＝ ．‎ ‎{答案}‎ ‎{解析}本题考查了比例的性质，直接运用比例的性质化简计算即可，因为＝1＋＝，所以＝，因此本题应填．‎ ‎{分值}3‎ ‎{章节:[1－27－3]图形的相似}‎ ‎{考点:比例的性质}‎ ‎{类别:常考题}‎ ‎{难度:2－简单}‎ ‎{题目}11．（2019年郴州T11）如图，直线 a，b 被直线 c，d 所截．若 a//b，∠1＝130°，∠2＝30°，则∠3 的度数为 度．‎ ‎（第11题图）‎ ‎{答案}100‎ ‎{解析}本题考查了平行线的性质以及三角形外角的性质，∵a∥b，∴∠1＝∠2＋∠3，又∵∠2＝30°，∴∠3＝∠1－∠2＝130°－30°＝100°，因此本题应填100．‎ ‎{分值}3‎ ‎{章节:[1－11－2]与三角形有关的角}‎ ‎{考点:三角形的外角}‎ ‎{考点:两直线平行同位角相等}‎ ‎{类别:常考题}‎ ‎{难度:2－简单}‎ ‎{题目}12．（2019年郴州T12）某校举行演讲比赛，七个评委对小明的打分如下： 9，8，7，6，9，9，7，这组数据的中位数是 ．‎ ‎{答案}8‎ ‎{解析}本题考查了中位数的概念，将一组数据从小到大（或从大到小）重新排列后，最中间的数（或最中间的两个数的平均数），叫做这组数据的中位数．将数据9，8，7，6，9，9，7，从小到大排列为：6，7，7，8，9，9，9，中间的数是8，即这组数据的中位数是8，因此本题应填8．‎ ‎{分值}3‎ ‎{章节:[1－20－1－2]中位数和众数}‎ ‎{考点:中位数}‎ ‎{类别:常考题}‎ ‎{难度:2－简单}‎ ‎{题目}13．（2019年郴州T13）某商店今年 6 月初销售纯净水的数量如下表所示：‎ 日期 ‎1‎ ‎2‎ ‎3‎ ‎4‎ 数量（瓶）‎ ‎120‎ ‎125‎ ‎130‎ ‎135‎ 观察此表，利用所学函数知识预测今年 6 月 7 日该商店销售纯净水的数量约为 瓶．‎ ‎{答案}150‎ ‎{解析}本题考查了函数的应用，由表格可知销售数量y与日期x之间的函数关系式为y＝120＋5（x－1）＝5x＋115，当x＝7时，y＝5×7＋115＝150，因此本题应填150．‎ ‎{分值}3‎ ‎{章节:[1－19－1－1]变量与函数}‎ ‎{考点:函数关系式}‎ ‎{考点:函数值}‎ ‎{类别:思想方法}‎ ‎{难度:2－简单}‎ ‎{题目}14．（2019年郴州T14）如图是甲、乙两人 6 次投篮测试（每次投篮 10 个）成绩的统计图，甲、乙两人测试成绩的方差分别记作、 ，则 （填“＞”“＝”或“＜”）‎ 测试次数 测试成绩/个 甲 乙 ‎（第14题图）‎ ‎{答案}＜‎ ‎{解析}本题考查了方差的计算，因为＝（8＋7＋8＋6＋9＋8）＝，＝〔（8－）2＋（7－）2＋（8－）2＋（6－）2＋（9－）2＋（8－）2〕＝，＝（7＋4＋7＋9＋5＋7）＝，＝〔（7－）2＋（4－）2＋（7－）2＋（9－）2＋（5－）2＋（7－）2〕＝，因为＞，所以＞，因此本题应填“＜”．‎ ‎{分值}3‎ ‎{章节:[1－20－2－1]方差}‎ ‎{考点:算术平均数}‎ ‎{考点:方差}‎ ‎{类别:常考题}‎ ‎{难度:2－简单}‎ ‎{题目}15．（2019年郴州T15）已知某几何体的三视图如图，其中主视图和左视图都是腰长为 5，底边长为 4 的等腰三角形，则该几何体的侧面展开图的面积是 ．（结果保留 π ）‎ ‎（第15题图）‎ ‎5‎ ‎5‎ ‎4‎ ‎4‎ ‎ ‎ ‎{答案}10π ‎{解析}本题考查了由三视图判断几何体，圆锥的计算．依题意，圆锥的地面周长为4π，圆锥的母线长为5，所以其侧面展开图为扇形，面积为×4π×5＝10π，因此本题应填10π．‎ ‎{分值}3‎ ‎{章节:[1－29－2]三视图}‎ ‎{考点:简单几何体的三视图}‎ ‎{考点:扇形的面积}{类别:常考题}‎ ‎{难度:2－简单}‎ 题目}16．（2019年郴州T16）如图，点 A，C 分别是正比例函数 y＝x 的图象与反比例函数 y＝的图象的交点，过 A点作 AD⊥ x 轴于点 D，过 C 点作 CB⊥ x 轴于点 B，则四边形 ABCD 的面积为 ．‎ ‎（第16题图）‎ ‎{答案}8‎ ‎{解析}本题考查了反比例函数与一次函数的交点问题，解方程组得或，所以A的坐标为（2，2），C的坐标为（－2，－2），又过 A点作 AD⊥ x 轴于点 D，过 C 点作 CB⊥ x 轴于点 B，所以B（－2，0），D（2，0），所以BD＝4，AD＝2，所以ABCD的面积＝AD·BD＝0，因此本题应填8．‎ ‎{分值}3‎ ‎{章节:[1－26－1]反比例函数的图像和性质}‎ ‎{考点:反比例函数与一次函数的综合}‎ ‎{考点:一次函数与几何图形综合}‎ ‎{考点:代数填空压轴}‎ ‎{考点:几何填空压轴}‎ ‎{类别:易错题}‎ ‎{难度:3－中等难度}‎ ‎{题型:4－解答题}三、解答题：本大题共10小题，合计82分．‎ ‎{题目}17．（2019年郴州T17）计算：‎ ‎{解析}本题考查了实数的运算，零指数幂，负整数指数幂，绝对值，特殊角的三角函数值．直接利用特殊角的三角函数值以及零指数幂的性质、绝对值的性质分别化简得出答案．‎ ‎{答案}解：原式＝1－2×＋－1＋2‎ ‎＝1－＋－1＋2‎ ‎＝2‎ ‎{分值}6‎ ‎{章节:[1－28－3]锐角三角函数}‎ ‎{难度:2－简单}‎ ‎{类别:常考题}‎ ‎{考点:简单的实数运算}‎ ‎{考点:二次根式的混合运算}‎ ‎{考点:特殊角的三角函数值}‎ ‎{题目}18．（2019年郴州T18）先化简，再求值：，其中a＝．‎ ‎{解析}本题考查了分式的化简求值，原式中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把a的值代入计算即可求值．‎ ‎{答案}解： 原式＝－‎ ‎＝‎ ‎＝‎ ‎＝．‎ ‎ 当a＝时，原式＝＝＝．‎ ‎{分值}6‎ ‎{章节:[1－15－2－2]分式的加减}‎ ‎{难度:2－简单}‎ ‎{类别:常考题}‎ ‎{考点:分式的混合运算}‎ ‎{考点:简单的实数运算}‎ ‎{题目}19．（2019年郴州T19）如图，□ABCD 中，点 E 是边 AD 的中点，连接 CE 并延长交 BA 的延长线于点 F，连接 AC，DF．‎ 求证：四边形 ACDF 是平行四边形．‎ ‎{解析}本题考查了平行四边形、平行线的判定，全等三角形的性质，解题的关键是得到AF∥CD，且AF＝CD．‎ ‎{答案}证明：∵ABCD是平行四边形，‎ ‎∴AB∥CD，即AF∥CD，‎ ‎∴∠AFE＝∠DCE ‎∵点 E 是边 AD 的中点，‎ ‎∴EF＝EC，‎ 又∵∠AEF＝∠DEC，‎ ‎∴△AEF≌△DEC，‎ ‎∴ AF＝DC ‎∴四边形 ACDF 是平行四边形．‎ ‎{分值}6‎ ‎{章节:[1－18－1－2]平行四边形的判定}‎ ‎{难度:3－中等难度}‎ ‎{类别:常考题}‎ ‎{考点:平行四边形边的性质}‎ ‎{考点:两直线平行内错角相等}‎ ‎{考点:全等三角形的判定ASA,AAS}‎ ‎{考点:全等三角形的性质}‎ ‎{考点:一组对边平行且相等的四边形是平行四边形}‎ ‎{题目}20．（2019年郴州T20）我市去年成功举办 2018 郴州国际休闲旅游文化节，获评“全国森林旅游示范市”．我市有 A，B，C，D，E 五个景区很受游客喜爱．一旅行社对某小区居民在暑假期间去 以上五个景区旅游（只选一个景区）的意向做了一次随机调查统计，并根据这个统计结果制作了如下两幅不完整的统计图：‎ ‎（1）该小区居民在这次随机调查中被调查到的人数是 人，m＝ ，并补全条形统计图；‎ ‎（2）若该小区有居民 1200 人，试估计去 B 地旅游的居民约有多少人？‎ ‎（3）小军同学已去过 E 地旅游，暑假期间计划与父母从 A，B，C，D 四个景区中，任 选两个去旅游，求选到 A，C 两个景区的概率．(要求画树状图或列表求概率)‎ ‎{解析}本题考查了扇形统计图；条形统计图；列表法与树状图法．（1）由D组人数及其所占百分比求得被调查人数，再用B组人数除以被调查人数所得的百分比求m，继而根据各组人数之和等于总人数求出C组的人数，从而补全条形统计图；（2）用样本估计总体，从而估计去 B 地旅游的居民人数；（3）依据树状图，可得共有12种等可能的情况，其中选中A、C的情况有2种，即可得选到 A，C 两个景区的概率．‎ ‎{答案}解：（1）有统计图可知：D组人数有20人，占调查人数的10％，‎ 所以被调查到的人数为 20÷10％＝200（人）‎ 又B组人数为70，所以占被调查人数的70÷200×100％＝35％，‎ 所以m＝35，‎ C组人数为：200－20－70－20－50＝40（人）‎ 补全的条形统计图为：‎ ‎ （2）若该小区有居民 1200 人，则去 B 地旅游的居民约有1200×＝420（人）；‎ ‎ （3）画树状图如下：‎ ‎ ‎ ‎ 可见，共有12种等可能的情况，其中选中A、C的情况有2种， ‎ ‎ 所以选到 A，C 两个景区的概率为．‎ ‎{分值}8‎ ‎{章节:[1－25－2]用列举法求概率}‎ ‎{难度:3－中等难度}‎ ‎{类别:常考题}‎ ‎{考点:两步事件不放回}‎ ‎{考点:扇形统计图}‎ ‎{考点:条形统计图}‎ ‎（第21题图）‎ ‎{题目}21．（2019年郴州T21）如图所示，巡逻船在 A 处测得灯塔 C 在北偏东 45°方向上，距离 A 处 30 km．在灯塔 C 的正南方向 B 处有一渔船发出求救信号，巡逻船接到指示后立即前往施救．已知 B 处 在 A 处的北偏东 60°方向上，这时巡逻船与渔船的距离是多少？（精确到 0.01 km．参考数据：≈1.414，≈ 1.732，≈ 2.449 ）‎ ‎{解析}本题考查了解直角三角形的应用－方向角问题．延长CB交东西方向线于点D，则AD＝AC·sin45°，AD＝AB·sin60°，从而得到AC·sin45°＝AB·sin60°，由于AC＝30km，sin45°＝，sin60°＝，因此可求得AB，此即巡逻船与渔船的距离．‎ ‎{答案}解：延长CB交东西方向线于点D，则AD＝AC·sin45°，AD＝AB·sin60°，‎ ‎ ∴AC·sin45°＝AB·sin60°，‎ 由于AC＝30km，sin45°＝，sin60°＝，‎ ‎∴AB＝＝＝10≈24.49（km）‎ 答：巡逻船与渔船的距离是24.49km．‎ ‎{分值}8‎ ‎{章节:[1－28－1－2]解直角三角形}‎ ‎{难度:3－中等难度}‎ ‎{类别:常考题}‎ ‎{考点:解直角三角形－方位角}‎ ‎{考点:解直角三角形}‎ ‎{题目}22．（2019年郴州T22）某小微企业为加快产业转型升级步伐，引进一批A，B两种型号的机器．已知一台A型机器比一台B型机器每小时多加工2个零件，且一台A型机器加工80个零件与一台B型机器加工60个零件所用时间相等．‎ ‎（1）每台A，B两种型号的机器每小时分别加工多少个零件？‎ ‎（2）如果该企业计划安排A，B两种型号的机器共10台一起加工一批该零件，为了如期完成任务，要求两种机器每小时加工的零件不少于72件，同时为了保障机器的正常运转，两种机器每小时加工的零件不能超过76件，那么A，B两种型号的机器可以各安排多少台？‎ ‎{解析}本题考查了分式方程的应用；一元一次不等式组的应用．（1）设一台A型号机器每小时加工x个零件，则一台B型机器每小时加工（x－2）个零件，根据一台A型机器加工80个零件与一台B 型机器加工60个零件所用时间相等可得出关于x的分式方程，解之经检验后即可得出结论；（2）利用两种机器每小时加工的零件不少于72件，不能超过76件，列方程组可得出结论．‎ ‎{答案}解：（1）设一台A型号机器每小时加工x个零件，则一台B型机器每小时加工（x－2）个零件，‎ 根据，解得x＝8‎ 经检验x＝8是原方程的解，‎ 所以A型机器每小时加工零件8个，B型机器每小时加工零件6个；‎ ‎ （2）设A型号机器安排y台，则B型号机器安排（10－y）台，‎ ‎ 依题意，可得 72≤8y＋6（10－y）≤76‎ ‎ 解得 6≤y≤8‎ ‎ 即y的可取值为：6，7，8‎ ‎ 所以A，B两种型号的机器可以作如下安排：‎ ① A型号机器6台，B型号机器4台；‎ ② A型号机器7台，B型号机器3台；‎ ③ A型号机器8台，B型号机器2台．‎ ‎{分值}8‎ ‎{章节:[1－15－3]分式方程}‎ ‎{难度:3－中等难度}‎ ‎{类别:常考题}‎ ‎{考点:其他分式方程的应用}‎ ‎{考点:一元一次不等式的整数解}‎ ‎{考点:一元一次不等式的应用}‎ ‎{题目}23．（2019年郴州T23）如图，已知 AB 是⊙O 的直径，CD 与⊙O 相切于点 D，且 AD//OC．‎ ‎（1）求证：BC 是⊙O 的切线；‎ ‎（2）延长 CO 交⊙O 于点 E．若∠CEB＝30°，⊙O 的半径为 2，求 的长．（结果保留 π ）‎ ‎（第23题图）‎ ‎{解析}本题考查了切线的判定与性质、全等三角形的判定与性质以及平行线的性质和弧长的计算．注意掌握辅助线的作法，注意掌握数形结合思想的应用是解决问题的关键．‎ ‎{答案}解：（1）证明：连接OD，如答图所示．‎ ‎（23题答图）‎ ‎∵AD//OC，‎ ‎∴∠COD＝∠ADO，∠COB＝∠DAO，‎ 又∵OA＝OD，∴∠ADO＝∠DAO，‎ ‎∴∠COD＝∠COB，‎ 在△COD和△COB中，‎ ‎∴△COD≌COB，‎ ‎∴∠CDO＝∠CBO，‎ 又CD 与⊙O 相切于点 D，‎ ‎∴∠CDO＝90°，‎ ‎∴∠CBO＝90°，‎ ‎∴BC 是⊙O 的切线；‎ ‎ （2）∵∠CEB＝30°，∴∠COB＝60°，‎ 由（1）知，∠COD＝∠COB，‎ ‎∴∠COD＝60°，‎ ‎∴∠DOB＝∠COD＋∠COB＝120°‎ ‎∵⊙O 的半径为 2，‎ ‎∴的长＝＝．‎ ‎{分值}8‎ ‎{章节:[1－24－2－2]直线和圆的位置关系}‎ ‎{难度:3－中等难度}‎ ‎{类别:常考题}‎ ‎{考点:两直线平行同位角相等}‎ ‎{考点:两直线平行内错角相等}‎ ‎{考点:全等三角形的判定SAS}‎ ‎{考点:全等三角形的性质}‎ ‎{考点:切线的性质}‎ ‎{考点:切线的判定}‎ ‎{考点:弧长的计算}‎ ‎{题目}24．（2019年郴州T24）若一个函数当自变量在不同范围内取值时，函数表达式不同，我们称这样的函数为分段函数．下面我们参照学习函数的过程与方法，探究分段函数 的图象与性质． ‎ 列表：‎ x ‎…‎ ‎－3‎ ‎－‎ ‎－2‎ ‎－‎ ‎－1‎ ‎－‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎…‎ y ‎…‎ ‎1‎ ‎2‎ ‎1‎ ‎0‎ ‎1‎ ‎2‎ ‎…‎ 描点：在平面直角坐标系中，以自变量 x 的取值为横坐标，以相应的函数值 y 为纵坐标，描出相应的点，如图所示．‎ ‎（1）如图，在平面直角坐标系中，观察描出的这些点的分布，作出函数图象；‎ ‎（2）研究函数并结合图象与表格，回答下列问题：‎ ‎①点A（－5，y1），B（－，y2），C（x1，），D（x2，6）在函数图象上，则 y1 y2 ， x1 x2 ；（填“＞”、“＝”或“＜”）‎ ‎②当函数值y＝2 时，求自变量 x 的值；‎ ‎③在直线x＝－1的右侧的函数图象上有两个不同的点 P( x3，y3 )，Q( x4，y4 ) ，且y3＝y4 ，求 x3＋x4的值；‎ ① 若直线 y＝a 与函数图象有三个不同的交点，求 a 的取值范围．‎ ‎{解析}本题考查了函数图象的一般画法，分段函数的增减性，绝对值的性质等内容．‎ ‎{答案}解：（1）根据列表、描点，可以做出函数图像，如下图：‎ ‎ ‎ ‎ （2）①由图象可知，当x≤－1时，函数值随x的增大而减小，‎ 因为A、B在函数图象上，且－5＜－＜－1， ‎ 所以y1＜y2．‎ 又因为＞2，6＞2，C、D在函数图象上，‎ 所以C、D在函数图象y＝x－1（x＞1）上，且函数值随x的增大而增大，‎ ‎∵＜6，∴x1＜x2．‎ 即这里的两空应填：＜；＜．‎ ‎ ②当y＝2时，若x≤－1，则有－＝2，解得x＝－1；‎ ‎ 若x＞－1时，则有|x－1|＝2，即x－1＝±2，‎ 解得x＝3或x＝－1（不合题意，舍去）‎ 综上所述，y＝2时，自变量x的值为－1或3．‎ ‎③若点 P( x3，y3 )，Q( x4，y4 ) 是直线x＝－1的右侧的函数图象上的两个不同的点，且y3＝y4 ，则|x3－1|＝|x4－1|，所以x3－1＝－（x4－1），‎ 所以x3＋x4＝2．‎ ‎④若直线 y＝a 与函数图象有三个不同的交点，‎ 通过观察函数图象可知：0＜a＜2．‎ ‎{分值}10‎ ‎{章节:[1－26－1]反比例函数的图像和性质}‎ ‎{难度:3－中等难度}‎ ‎{类别:高度原创}‎ ‎{考点:分段函数}‎ ‎{考点:函数图象上的点}‎ ‎{考点:一次函数的性质}‎ ‎{考点:反比例函数的性质}‎ ‎{题目}25．（2019年郴州T25）如图1，矩形ABCD中，点E为AB边上的动点（不与A，B重合），把△ADE沿DE翻折，点A的对应点为A1 ，延长EA1交直线DC于点F，再把∠BEF折叠，使点B的对应点B1落在EF上，折痕EH交直线BC于点H．‎ ‎（1）求证：△A1DE∽△B1EH；‎ ‎（2）如图2，直线MN是矩形ABCD的对称轴，若点A1恰好落在直线MN上，试判断△DEF的形状，并说明理由；‎ ‎（3）如图3，在（2）的条件下，点G为△DEF内一点，且∠DGF＝150°，试探究DG，EG，FG的数量关系．‎ ‎（第25题图）‎ A1‎ B1‎ A1‎ B1‎ A1‎ B1‎ ‎{解析}本题考查了相似三角形的判定，轴对称图形的性质，勾股定理等内容．‎ ‎{答案}解：（1）证明：由于△ADE沿DE翻折，点A的对应点为A1 ，‎ ‎ ∴∠AED＝∠A1ED 再把∠BEF折叠，使点B的对应点B1落在EF上，折痕EH交直线BC于点H．‎ ‎∴∠BEH＝∠FEH，‎ 又∠AED＋∠A1ED＋∠BEH＋∠FEH＝180°‎ ‎∴∠A1ED＋∠FEH＝90°‎ ‎∵ABCD是矩形，∴∠EDA1＋∠A1ED＝180°－90°＝90°‎ ‎∴∠∠EDA1＝∠FEH，‎ 又∠DAE＝∠DA1E＝∠HBE＝∠HB1E＝90°，‎ ‎∴△A1DE∽△B1EH；‎ ‎（2）△DEF是等边三角形，理由如下：‎ ‎∵MN是矩形的对称轴，点A1恰好落在直线MN上，‎ ‎∴，即EA1＝A1F，‎ 又∠DA1E＝90°‎ ‎∴DA1是EF的垂直平分线，‎ ‎∴DE＝DF，∠EDA1＝∠FDA1，即△DEF是等腰三角形．‎ ‎∵△A1DE是△ADE沿DE翻折得到的，‎ ‎∴∠ADE＝∠A1DE＝∠A1DF＝∠ADC＝30°，‎ ‎∴∠EDF＝60°，‎ 即△DEF是等边三角形．‎ ‎ （3）DG，EG，FG所满足的数量关系为：DG2＋FG2＝EG2．‎ ‎ 理由如下：‎ 将△EDG绕点E逆时针旋转60°，从而旋转后的ED将会和EF重合，同时G点落在了 G1的位置（如答图）．‎ 由于△EFG1是由△EDG旋转过去得到的，‎ 因此FG1＝DG，EG＝EG1，∠GEG1＝60°．‎ ‎∴GG1＝EG，‎ 所以△GFG1的三边长事实上分别等于GF、GD、GE。‎ 又∠GFG1＝∠G1FE＋∠GFE ‎＝∠GDE＋∠GFE ‎＝（60°－∠GDF）＋（60°－∠GFD）‎ ‎＝120°－（∠GDF＋∠GFD）‎ ‎＝120°－（180°－∠DGF）‎ ‎＝120°－（180°－150°）‎ ‎＝90°‎ ‎ 所以△GFG1是直角三角形，且GF2＋G1F2＝GG12,‎ ‎ 即DG2＋GF2＝GE2．‎ ‎{分值}10‎ ‎{章节:[1－27－1－1]相似三角形的判定}‎ ‎{难度:4－较高难度}‎ ‎{类别:发现探究}‎ ‎{考点:相似三角形的判定（两角相等）}‎ ‎{考点:垂直平分线的性质}‎ ‎{考点:等边三角形的判定}‎ ‎{考点:轴对称的性质}‎ ‎{考点:旋转的性质}‎ ‎{考点:勾股定理}‎ ‎{题目}26．（2019年郴州T26）已知抛物线y＝ax2 ＋ bx ＋ 3与x轴分别交于A（－3，0），B（1，0）两点，与y轴交于点C．‎ ‎（1）求抛物线的表达式及顶点D的坐标；‎ ‎（2）点F是线段AD上一个动点．‎ ‎①如图1，设k＝，当 k 为何值时，CF＝AD ？‎ ‎②如图2，以A，F，O为顶点的三角形是否与△ABC相似？若相似，求出点F的坐标；若不相似，请说明理由．‎ A B O C D F y y y O O A A B B C C D D F F ‎{解析}本题考查了有关二次函数的综合性问题．解题的关键在于熟练掌握二次函数图象上点的坐标特征、相似三角形的判定和性质；会利用待定系数法求函数解析式；理解坐标与图形性质；会运用分类讨论的思想解决数学问题． ‎ ‎{答案}解：（1）因为抛物线y＝ax2 ＋ bx ＋ 3与x轴分别交于A（－3，0），B（1，0）两点，‎ ‎ ∴，解得 ‎∴抛物线的表达式为y＝－x2－2x＋3，‎ ‎∵y＝－x2－2x＋3＝－（x＋1）2＋4，‎ ‎∴抛物线的顶点D的坐标为（－1，4）．‎ ‎（2）①∵A、D两点的坐标分别为：A（－3，0），D（－1，4），‎ ‎∴可设过A、D两点的直线的表达式为y＝mx＋n，‎ 依题意，得，解得 ‎∴直线AD的表达式为y＝2x＋6．‎ 又∵抛物线y＝ax2 ＋ bx ＋ 3与y轴的交点为C，‎ ‎∴C点的坐标为（0，3），‎ ‎∴AD2＝[－3－（－1）]2＋（0－4）2＝20，‎ ‎ AC2＝（－3－0）2＋（0－3）2＝18，‎ ‎ DC2＝（－1－0）2＋（4－3）2＝2，‎ 即AD2＝AC2＋DC2，‎ ‎∴△ACD是直角三角形，且∠ACD＝90°，‎ 若CF＝AD，则点F为AD的中点，‎ 此时，k＝＝，‎ ‎∴当k＝时，CF＝AD．‎ ‎②因为点F在AD上，所以可设F点的坐标为（t，2t＋6）‎ ‎∴AF＝，‎ ‎ OF＝‎ ‎ OA＝3‎ 由（2）①知△ABC各边的长为AC＝，BC＝，AB＝4，‎ ‎ 又tan∠DAC＝＝＝，tan∠OCB＝＝‎ ‎∴∠DAC＝∠OCB，‎ ‎∵OA＝OC＝3，∴∠OAC＝∠OCA ‎∴∠DAO＝∠DAC＋∠OAC＝∠OCB＋∠OCA＝∠ACB，‎ （i） 当时，我们有，解得t＝－2‎ 即当t＝－2时，△OFA∽△ABC，此时F点的坐标为（－2，2）；‎ ‎（ii）当时，我们有，解得t＝－，‎ ‎ 即当t＝－时，△FOA∽△ABC，此时点F的坐标为（－，）；‎ ‎ 综上所述，当点F的坐标为（－2，2）或（－，）时，以A，F，O为顶点的三角形是否与△ABC相似．‎ ‎{分值}12‎ ‎{章节:[1－27－1－1]相似三角形的判定}‎ ‎{难度:5－高难度}‎ ‎{类别:思想方法}‎ ‎{考点:代数综合}‎ ‎{考点:二次函数y＝ax2＋bx＋c的性质}‎ ‎{考点:二次函数的三种形式}‎ ‎{考点:二次函数中讨论相似}‎ ‎{考点:相似三角形的判定（两边夹角）}‎ ‎{考点:勾股定理}‎