第13章《全等三角形》培优习题4：全等三角形的判定—边边边公理 4页

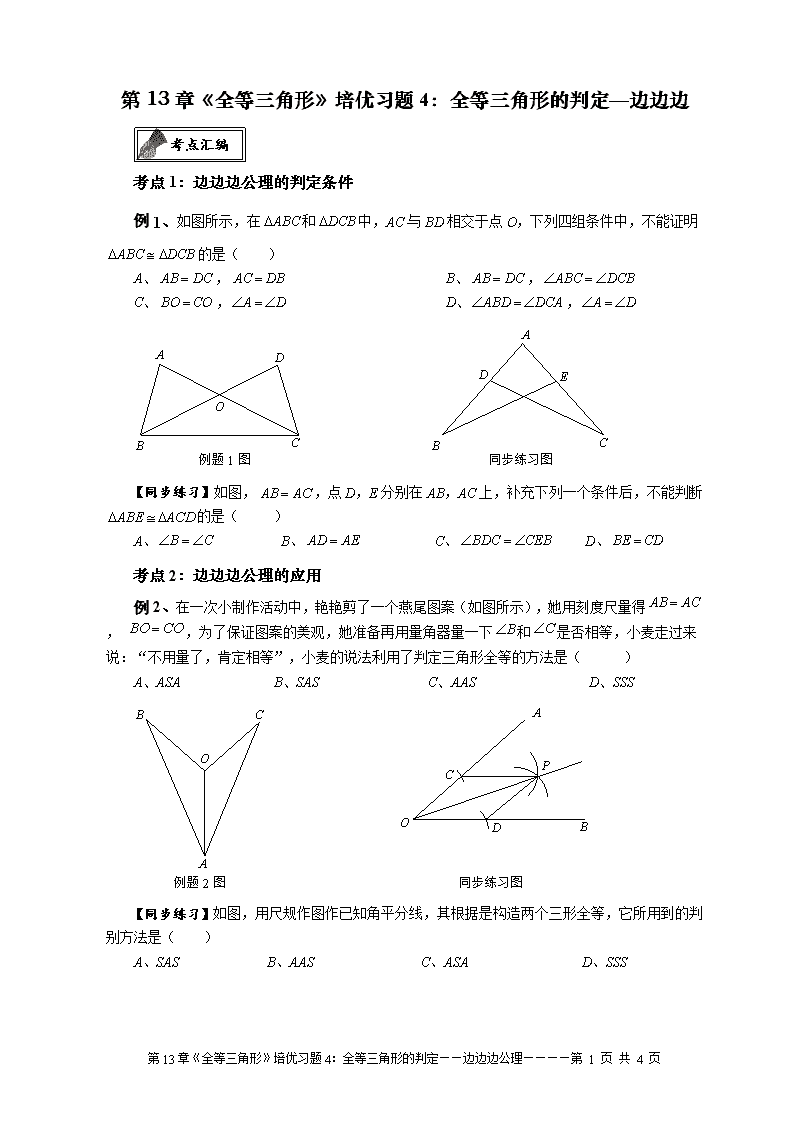
第 13 章《全等三角形》培优习题 4：全等三角形的判定——边边边公理————第 1 页 共 4 页 第 13 章《全等三角形》培优习题 4：全等三角形的判定—边边边 考点 1：边边边公理的判定条件 例 1、如图所示，在 ABC 和 DCB 中，AC 与 BD 相交于点 O，下列四组条件中，不能证明 DCBABC  的是（ ） A、 DCAB  ， DBAC  B、 DCAB  ， DCBABC  C、 COBO  ， DA  D、 DCAABD  ， DA  例题 1 图 O B C A D 同步练习图 E B C A D 【同步练习】如图， ACAB  ，点 D，E 分别在 AB，AC 上，补充下列一个条件后，不能判断 ACDABE  的是（ ） A、 CB  B、 AEAD  C、 CEBBDC  D、 CDBE  考点 2：边边边公理的应用 例 2、在一次小制作活动中，艳艳剪了一个燕尾图案（如图所示），她用刻度尺量得 ACAB  ， COBO  ，为了保证图案的美观，她准备再用量角器量一下 B 和 C 是否相等，小麦走过来说： “不用量了，肯定相等”，小麦的说法利用了判定三角形全等的方法是（ ） A、ASA B、SAS C、AAS D、SSS 例题 2 图 O B C A P D 同步练习图 O B C A 【同步练习】如图，用尺规作图作已知角平分线，其根据是构造两个三形全等，它所用到的判 别方法是（ ） A、SAS B、AAS C、ASA D、SSS 考点汇编 第 13 章《全等三角形》培优习题 4：全等三角形的判定——边边边公理————第 2 页 共 4 页 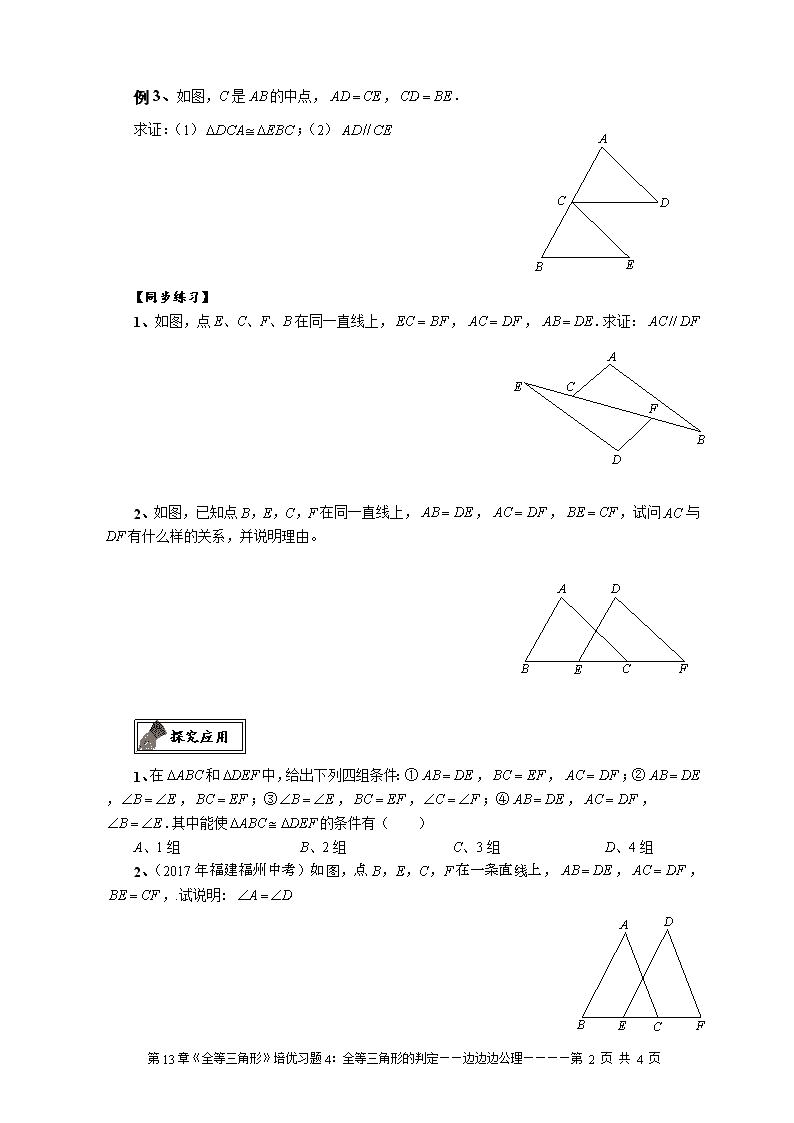例 3、如图，C 是 AB 的中点， CEAD  ， BECD  . 求证：（1） EBCDCA  ；（2） CEAD // 【同步练习】 1、如图，点 E、C、F、B 在同一直线上， BFEC  ， DFAC  ， DEAB  .求证： DFAC // 2、如图，已知点 B，E，C，F 在同一直线上， DEAB  ， DFAC  ， CFBE  ，试问 AC 与 DF 有什么样的关系，并说明理由。 1、在 ABC 和 DEF 中，给出下列四组条件：① DEAB  ， EFBC  ， DFAC  ；② DEAB  ， EB  ， EFBC  ；③ EB  ， EFBC  ， FC  ；④ DEAB  ， DFAC  ， EB  . 其中能使 DEFABC  的条件有（ ） A、1 组 B、2 组 C、3 组 D、4 组 2、（2017 年福建福州中考）如图，点 B，E，C，F 在一条直线上， DEAB  ， DFAC  ， CFBE  ，. 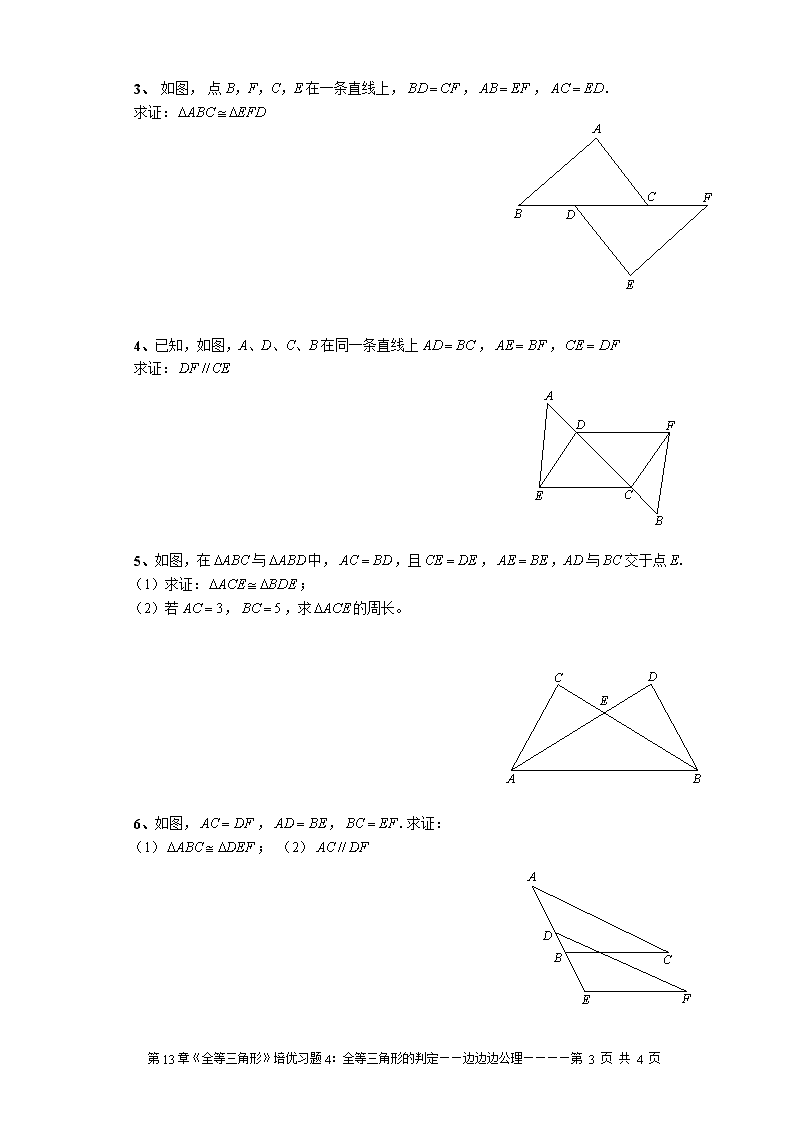试说明: DA  探究应用 E D B C A F B E D C A FB E D C A FC A EB D 第 13 章《全等三角形》培优习题 4：全等三角形的判定——边边边公理————第 3 页 共 4 页 3、 如图， 点 B，F，C，E 在一条直线上， CFBD  ， EFAB  ， EDAC  . 求证： EFDABC  4、已知，如图，A、D、C、B 在同一条直线上 BCAD  ， BFAE  ， DFCE  求证： CEDF // 5、如图，在 ABC 与 ABD 中， BDAC  ，且 DECE  ， BEAE  ，AD 与 BC 交于点 E. （1）求证： BDEACE  ； （2）若 3AC ， 5BC ，求 ACE 的周长。 6、如图， DFAC  ， BEAD  ， EFBC  .求证： （1） DEFABC  ； （2） DFAC // FC A E B D F C A E B D C A E B D F C A E B D 第 13 章《全等三角形》培优习题 4：全等三角形的判定——边边边公理————第 4 页 共 4 页 7、如图，点 B，E，C，F 在一条直线上， DEAB  ， DFAC  ， CFBE  .试说明： （1） DEFABC  ； （2） EGCA  8、如图， ADAB  ， DCBC  ，点 E 在 AC 上。 （1）求证：AC 平分 BAD ； （2）求证： DEBE  9、如图，点 A、D、C、F 在同一条直线上， CFAD  ， DEAB  ， EFBC  （1）求证： DEFABC  ； （2）若  60A ，  80B ，求 F 的度数。 10、如图所示，D 是 BC 上一点， ADAB  ， DEBC  ， AEAC  ，AC 与 DE 交于点 F. 求证： EC  G FC A EB D C A EB D FCA EB D F C A E B D