2012年山东省烟台市中考数学真题 7页

2012 年烟台市初中学生学业考试 数 学 试 题 说明： 1．本试题分为Ⅰ卷和Ⅱ卷两部分．第Ⅰ卷为选择题，第Ⅱ卷为非选择题，考试时间 120 分钟，满分 120 分. 2．答题前将密封线内的项目填写清楚． 3．考试过程中允许考生进行剪、拼、折叠等实验． 第Ⅰ卷 注意事项： 请考生将自己的姓名、准考证号、考试科目涂写在答题卡上.选择题选出答案后,用 2B 铅笔把答题卡对应题目的答案标号涂黑,不能答在本试题上.如要改动,必须先用橡皮擦干净, 再选涂另一个答案. 一、选择题（本题共 12 小题，每小题 3 分，共 36 分）每小题都给出标号为 A，B，C，D 四个备选答案，其中有且只有一个是正确的. 1． 4 的值是（ ）． （A）4 （B）2 （C） 2 （D） 2 2．如图是几个小正方体组成的一个几何体，这个几何体的俯视图是（ ）. 3．不等式组 21x x    ≤3, -1 的解集在数轴上表示正确的是（ ）． 4．如图，所给图形中是中心对称图形但不是轴对称图形的是（ ）． 5．已知二次函数 22( 3) 1yx   ．下列说法：①其图象的开口向下；②其图象的对称轴为 （第 2 题图） （第 9 题图） （第 4 题图） （A） （B） （C） （D） 直线 3x  ；③其图象顶点坐标为 (3 1)， ；④当 3x  时，y 随 x 的增大而减小．则其中说 法正确的有（ ）． （A）1 个 （B）2 个 （C）3 个 （D）4 个 6．如图，在平面直角坐标中，等腰梯形 ABCD的下底在 x 轴上，且 B 点坐标为(4 0)， ， D 点坐标为(0 3)， ，则 AC 长为（ ）． （A）4 （B）5 （C）6 （D）不能确定 7．在共有１５人参加的“我爱祖国”演讲比赛中，参赛选手要想知道自己是否能进入前 8 名，只需要了解自己的成绩以及全部成绩的（ ）． （A）平均数 （B）众数 （C）中位数 （D）方差 8．下列一元二次方程两实数根和为 4 的是（ ）． （A） 2 2 4 0xx   （B） 2 4 4 0xx   （C） 2 4 10 0xx   （D） 2 4 5 0xx   9．一个由小菱形组成的装饰链，断去了一部分，剩下部分如图所示，则断去部分的小菱形 的个数可能是（ ）． （A）3 （B）4 （C）5 （D）6 10．如图， 1O⊙ ， O⊙ ， 2O⊙ 的半径均为 2cm， 3O⊙ ， 4O⊙ 的半 径均为 1cm， 与其他 4 个圆均相外切，圆形既关于 12OO 所在直 线对称，又关于 34OO 所在直线对称，则四边形 1 2 3 4O O O O 的面积为 （ ）． （A） 212cm （B） 224cm （C） 236cm （D） 248cm 11.如图是跷跷板示意图，横板 AB 绕中点O 上下转动，立柱OC 与地面垂直，设 B 点的最 大高底为 1h ．若将横板 AB 换成横板 AB，且 ＝ 2AB ，O 仍为 的中点，设 B点 的最大高度为 2h ，则下列结论正确的是（ ）． （A） 212hh （B） 211.5hh （C） 21hh （D） 21 1 2hh 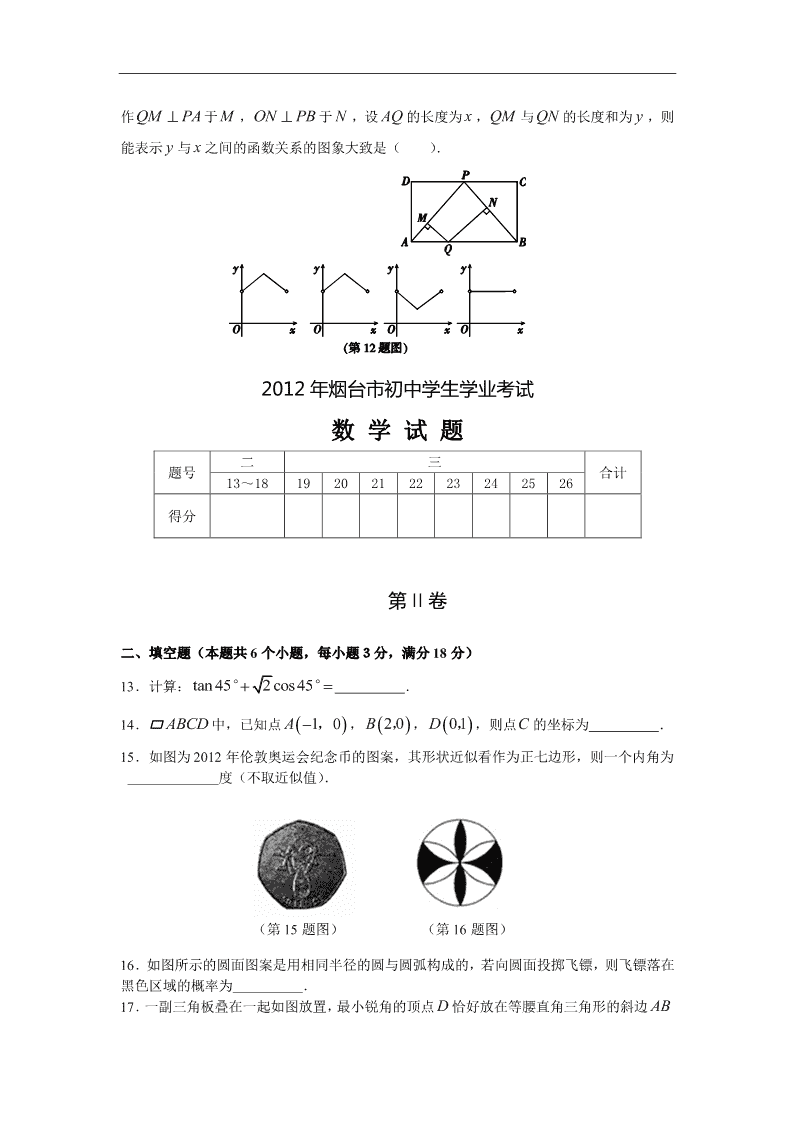12．如图，矩形 ABCD中，P 为CD 中点，点Q 为 AB 上的动点（不与 AB， 重合），过 Q 作QM PA 于 M ，ON PB 于 N ，设 AQ 的长度为 x ，QM 与QN 的长度和为 y ，则 能表示 y 与 x 之间的函数关系的图象大致是（ ）． 2012 年烟台市初中学生学业考试 数 学 试 题 题号 二 三 合计 13～18 19 20 21 22 23 24 25 26 得分 第Ⅱ卷 二、填空题（本题共 6 个小题，每小题３分，满分 18 分） 13．计算： tan 45 2 cos45° ° ． 14． ABCD 中，已知点  1A  ，0 ，  20B ， ，  01D ， ，则点C 的坐标为 ． 15．如图为 2012 年伦敦奥运会纪念币的图案，其形状近似看作为正七边形，则一个内角为 度（不取近似值）． 16．如图所示的圆面图案是用相同半径的圆与圆弧构成的，若向圆面投掷飞镖，则飞镖落在 黑色区域的概率为 ． 17．一副三角板叠在一起如图放置，最小锐角的顶点 D 恰好放在等腰直角三角形的斜边 AB （第 15 题图） （第 16 题图） 上， BC 与 DE 交于点 M ，如果 100ADF°，那么 BMD 为 度． 18．如图，在 Rt ABC△ 中， 90C °， 30A °， 2AB  ，将 ABC△ 绕项点 A 顺时 针方向旋转至 AB C△ 的位置， B A C， ， 三点共线，则线段 BC 扫过的区域面积 为 ． 三、解答题（本大题共 8 个小题，满分 66 分） 19．（ 本题满分 5 分）化简： 2 22 8 4 41 4 4 2 aa a a a a    ． 20．（ 本题满分 6 分） 第三届亚洲沙滩运动会服务中心要在某校选拨一名志愿者．经笔试、面试，结果小明和小颖 并例第一．评委会决定通过抓球来确定人选．抓球规则如下：在不透明的布袋里装有除颜色 之外均相同的 2 个红球和 1 个绿球，小明选取出一个球，记住颜色放回，然后小颖再取出一 个球．若取出的球都是红球，则小明胜出；若取出的球是一红一绿，则小颖胜出．你认为这 个规则对双方公平吗？请用列表法或画树状图的方法进行分析． 21．（ 本题满分 8 分） 某市为了鼓励居民节约用电，采用分段计费的方法按月计算每户家庭的电费．月用电量不超 过 200 度时，按 0.55 元/度计费；月用电量超过 200 度时，其中的 200 度仍按 0.55 元/度计 费，超过部分按 0.70 元/度计费．设每户家庭用电量为 x 度时，应交电费 y 元． （1）分别求出0 200x≤ ≤ 和 200x  时， y 与 x 的函数表达式； （2）小明家 5 月份交纳电费 117 元，小明家这个月用电多少度？ 22．（ 本题满分 9 分） 某市园林处去年植树节在滨海路两侧栽了 A B C， ， 三个品种的树苗，栽种的 三 个品种树苗数量．．．．的扇形统计图如图（1），其中 B 种树苗数量对应的扇形圆心角为120°．今 年植树节前管理员调查了这三个品种树苗的成活率情况，准备今年从三个品种中选成活率最 高的品种再进行栽种．经调查得知： A 品种的成活率为 85%，三个品种的总成活率为 89%， 但三个品种树苗成活数量．．．．．．统计图尚不完整，如图（2）. 请你根据以上信息帮管理员解决下列问题： （1）三个品种树苗去年共栽多少棵？ （2）补全条形统计图，并通过计算，说明今年应栽哪个品种的树苗． 23．（ 本题满分 8 分） 如图，在平面直角坐标系中， AB， 两点的纵坐标分别为 7 和 1，直线 AB 与 y 轴所夹锐角 为 60°． （1）求线段 AB 的长； （2）求经过 AB， 两点的反比例函数的解析式． 24．（ 本题满分 8 分） 如图， AB 为 O⊙ 的直径，弦CD AB ，垂足为点 E ，CF AF ，且CF CE ． （1）求证：CF 是 O⊙ 的切线； （2）若 2sin 5BAC，求 CBD ABC S S △ △ 的值． 25．（ 本题满分 10 分） （1）问题探究 如图 1，分别以 ABC△ 的边 AC 与边 BC 为边，向 ABC△ 外作正方形 11ACD E 和正方形 22BCD E ，过点C 作直线 KH 交 AB 于点 H ，使 1AHK ACD   ．作 1D M KH ， 2D N KH ，垂足分别为点 MN， ．试探究线段 1DM与线段 2DN的数量关系，并加以证 明． （2）拓展延伸 ①如图 2，若将“问题探究”中的正方形改为正三角形，过点C 作直线 12KH ， 22KH，分 别交直线 AB 于点 1H ， 2H ，使 1 1 2 2 1AH K BH K ACD     ，作 1 1 1D M K H ， 2 2 2D N K H ，垂足分别为点 MN， ， 12D M D N 是否仍成立？若成立，给出证明；若 不成立，说明理由． ②如图３，若将①中的“正三角形”改为“正五边形”，其他条件不变， 12D M D N 是否 仍成立？（要求：在图 3 中补全图形，注明字母，直接写出结论，不需证明） 26．（ 本题满分 12 分）如图， 在平面直角坐标系中，已知矩形 ABCD的三个顶点 (10)B ， ， (3 0)C ， ， (3 4)D ， ，以 A 为顶点的抛物线 2y ax bx c   过点C ，动点 P 从点 出发，沿 线段 AB 向点 B 运动．同时动点Q 从点C 出发，沿线段CD 向点 D 运动，点 PQ， 的运动 速度均为每秒 1 个单位．运动时间为t 秒，过点 P 作 PE AB 交 AC 于点 E ． （1）直接写出点 A 的坐标，并求出抛物线的解析式； （2）过点 E 作 EF AD 于 F ，交抛物线于点G ，当t 为何值时， ACG△ 的面积最大？ 最大值为多少？ （3）在动点 PQ， 运动的过程中，当t 何值时，在矩形 ABCD内（包括边界）存在点 H ， 使以C Q E H， ， ， 为顶点的四边形为菱形？请直接写出t 的值．