2020年湖北省襄阳市谷城县中考数学模拟试卷(5月份) (含解析) 23页

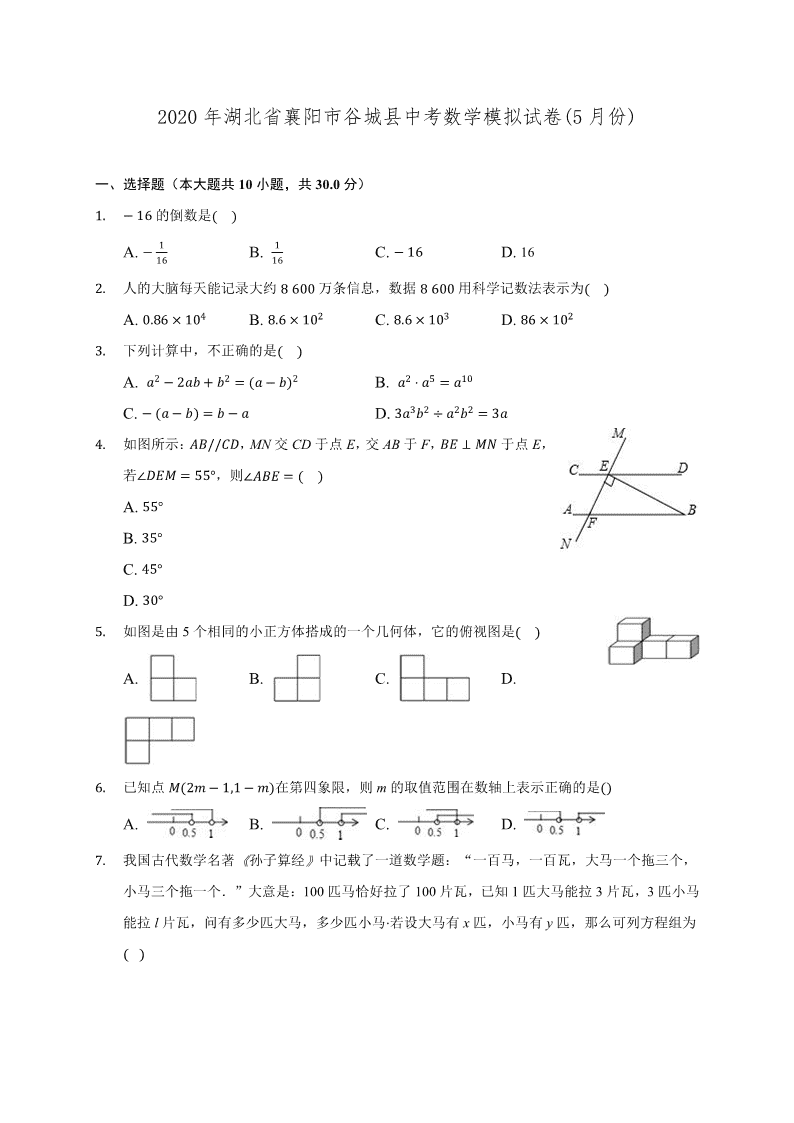
2020 年湖北省襄阳市谷城县中考数学模拟试卷(5 月份) 一、选择题（本大题共 10 小题，共 30.0 分） 1. 1䁜 的倒数是 A. 1 1䁜 B. 1 1䁜 C. 1䁜 D. 16 2. 人的大脑每天能记录大约 䁜香香 万条信息，数据 䁜香香 用科学记数法表示为 A. 香.䁜 1香 B. .䁜 1香 2 C. .䁜 1香 D. 䁜 1香 2 . 下列计算中，不正确的是 A. 2 2ܽ ܽ 2 ܽ 2 B. 2 1香 C. ܽ ܽ D. ܽ 2 2 ܽ 2 . 如图所示： ሻܾ ，MN 交 CD 于点 E，交 AB 于 F， ሻ 于点 E， 若 ܾ ，则 ሻ A. B. C. D. 香 . 如图是由 5 个相同的小正方体搭成的一个几何体，它的俯视图是 A. B. C. D. 䁜. 已知点 2ʹ 11 ʹ 在第四象限，则 m 的取值范围在数轴上表示正确的是 A. B. C. D. 7. 我国古代数学名著《孙子算经》中记载了一道数学题：“一百马，一百瓦，大马一个拖三个， 小马三个拖一个．”大意是：100 匹马恰好拉了 100 片瓦，已知 1 匹大马能拉 3 片瓦，3 匹小马 能拉 l 片瓦，问有多少匹大马，多少匹小马 若设大马有 x 匹，小马有 y 匹，那么可列方程组为 A. 1香香 1香香 B. 1香香 1 1香香C. 1香香 1香香 D. 1香香 1香香 . 下列说法正确的是 A. “买中奖率为 1 1香 的奖券 10 张，中奖”是必然事件 B. “汽车累积行驶 10000km，从未出现故障”是不可能事件 C. 襄阳气象局预报说“明天的降水概率为 7香ࣃ ”，意味着襄阳明天一定下雨 D. 若两组数据的平均数相同，则方差小的更稳定 9. 如图， ሻ 中， ሻ ， 72 ，AB 的垂直平分线 DE 交 AC 于 D，交 AB 于 E，则 ሻܾ 的度数为 A. 䁜B. 䁜香C. 72D. 2 1香. 如图，四边形 ABCD 内接于 ， ሻ 9香 ， ܾ 1香 ， ܾ ， 则 的半径长为 A. 2 .B. 2 .C. .D. .二、填空题（本大题共 6 小题，共 18.0 分） 11. 已知一元二次方程 2 香 有两个不相等的实数根，则 k 的取值范围______． 12. 对正有理数 a、b 定义运算 如下： ܽ ܽ 2 ܽ ，则 ______ ． 1. 在 1 、3、 2 这三个数中，任选两个数的积作为 k 的值，能使反比例函数 的图象位于第 一、三象限的概率是_________． 1. 把抛物线 2 向上平移 3 个单位长度后，所得的函数解析式为______． 1. 如图，将三角形 AOC 绕点 O 顺时针旋转 12香 得三角形 BOD， 已知 ， 1 ，那么图中阴影部分的面积为________ . 结 果保留 1䁜. 如图，在矩形 ABCD 中， ሻ ， ሻ 䁜 ，若点 E 是边 CD 的中点， 连接 AE，过点 B 作 ሻ 于点 F，则 BF 的长为____． 三、解答题（本大题共 9 小题，共 72.0 分） 17. 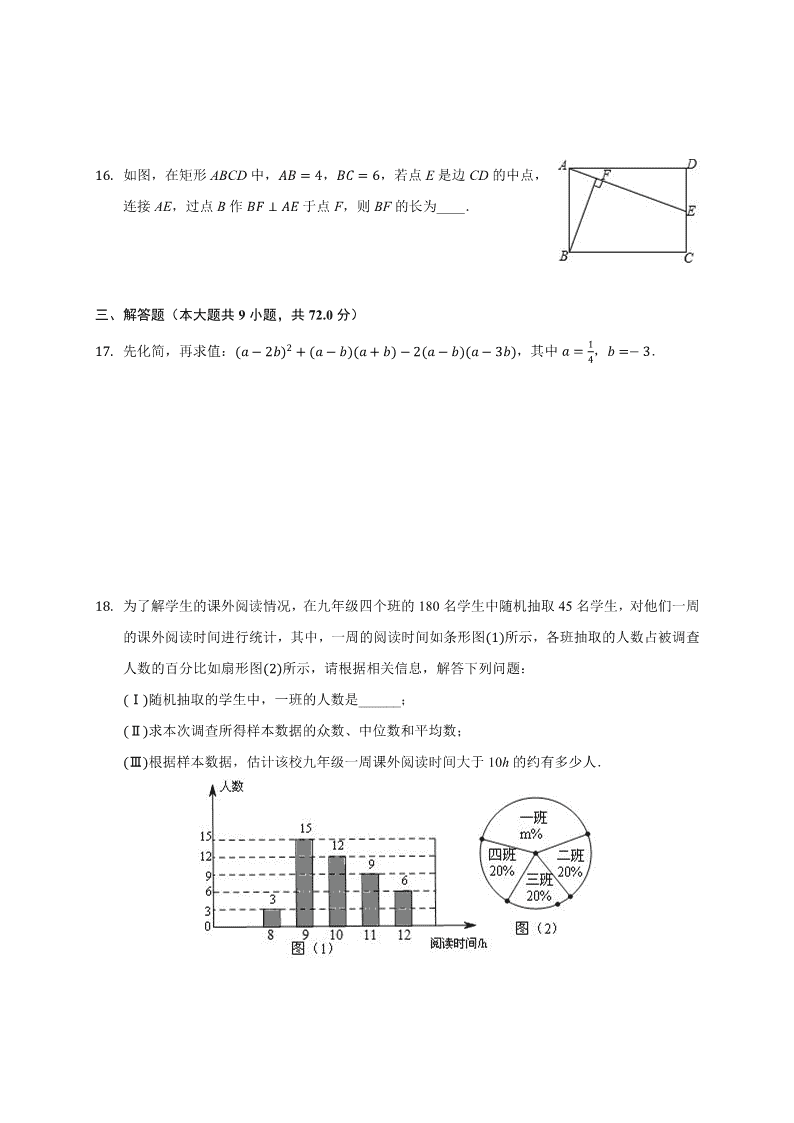先化简，再求值： 2ܽ 2 ܽ ܽ 2 ܽ ܽ ，其中 1 ， ܽ ． 1. 为了解学生的课外阅读情况，在九年级四个班的 180 名学生中随机抽取 45 名学生，对他们一周 的课外阅读时间进行统计，其中，一周的阅读时间如条形图 1 所示，各班抽取的人数占被调查 人数的百分比如扇形图 2 所示，请根据相关信息，解答下列问题： Ⅰ 随机抽取的学生中，一班的人数是______； Ⅱ 求本次调查所得样本数据的众数、中位数和平均数； Ⅲ 根据样本数据，估计该校九年级一周课外阅读时间大于 10h 的约有多少人． 19. 经过建设者三年多艰苦努力地施工，贯通我市的又一条高速公路“遂内高速公路”于 2012 年 5 月 9 日全线通车．已知原来从遂宁到内江公路长 150km，高速公路路程缩短了 30km，如果一辆 小车从遂宁到内江走高速公路的平均速度可以提高到原来的 1. 倍，需要的时间可以比原来少 用 1 小时 10 分钟．求小汽车原来和现在走高速公路的平均速度分别是多少？ 2香. 如图，小莹在数学综合实践活动中，利用所学的数学知识对某小 区居民楼 AB 的高度进行测量，先测得居民楼 AB 与 CD 之间的距 离 AC 为 35m，后站在 M 点处测得居民楼 CD 的顶端 D 的仰角为 ，居民楼 AB 的顶端 B 的仰角为 ，已知居民楼 CD 的高度 为 1䁜.䁜ʹ ，小莹的观测点 N 距地面 1.䁜ʹ. 求居民楼 AB 的高度 精确 到 ʹ. 参考数据： ݅ 香.2 ， ݋ 香.7 ， . ． 21. 如图，一次函数 2 与反比例函数 香 的图象交于Ａ ʹ䁜 ，Ｂ 两点． 1 求反比例函数的解析式 2 根据图象直接写出关于 x 的不等式 2 香 的解集． 22. 如图，AB 是 的直径，点 D，E 在 上， 2ሻܾ ，点 C 在 AB 的延长线上， ሻܾ ． 1 求证：CE 是 的切线； 2 若 ሻ 2 ， 1 ，求 的半径长． 23. 霍邱县三流乡开展产业扶贫，鼓励农民养殖龙虾，去年喜获丰收，今年随着各地龙虾节的火热 举办，该乡某龙虾养殖大户为了发挥技术优势，以 16 元 ㄠ 的价格，一次性收购了 10000kg 小 龙虾，计划养殖一段时间后再出售．已知这批小龙虾每天需要养殖成本 600 元．设这批小龙虾 放养 t 天后的质量为 akg，销售单价为 y 元 ㄠ ，根据往年的行情预测，a 与 t 的函数关系为 1香香香香香 2香 1香香 香香香2香 香 ，y 与 t 的函数关系如图所示． 1 求 y 与 t 间的函数表达式； 2 如果将这批小龙虾放养 t 天后一次性出售所得利润为 W 元，问该龙虾养殖大户将这批小龙虾 放养多少天后一次性出售所得利润最大？最大利润是多少？ 总成本 放养总费用 收购成本；利润 销售总额 总成本 24. 阅读材料：三角形的三条中线必交于一点，这个交点称为三角形的重心． 1 特例感知：如图 一 ，已知边长为 2 的等边 ሻ 的重心为点 O，求 ሻ 与 ሻ 的面积． 2 性质探究：如图 二 ，已知 ሻ 的重心为点 O，请判断 ܾ 、 ሻ ሻ 是否都为定值？如果是， 分别求出这两个定值；如果不是，请说明理由． 性质应用：如图 三 ，在正方形 ABCD 中，点 E 是 CD 的中点，连接 BE 交对角线 AC 于点 M． 若正方形 ABCD 的边长为 4，求 EM 的长度； 若 1 ，求正方形 ABCD 的面积． 25. 如图，在平面直角坐标系中，抛物线 2 ܽ 经过 香 ， ሻ1香 两点，其顶点为 D，连接 AD，点 P 是线段 AD 上一个动点 不与 AD 重合 ． 1 求抛物线的函数解析式，并写出顶点 D 的坐标； 2 如图 1，过点 P 作 轴于点 . 求 面积 S 的最大值； 如图 2，抛物线上是否存在一点 Q，使得四边形 OAPQ 为平行四边形？若存在求出 Q 点坐标， 若不存在请说明理由． 【答案与解析】 1.答案：A 解析：【试题解析】 解： 1䁜 的倒数是 1 1䁜 ， 故选：A． 根据乘积为 1 的两个数互为倒数，可得答案． 本题考查了倒数，分子分母交换位置是求一个数的倒数的关键． 2.答案：C 解析：解：数据 8600 用科学记数法表示为 .䁜 1香 . 故选 C． 科学记数法就是将一个数字表示成 1香 的 n 次幂的形式，其中 1 1香 ，n 表示整数．n 为整 数位数减 1，即从左边第一位开始，在首位非零的后面加上小数点，再乘以 10 的 n 次幂． 用科学记数法表示一个数的方法是 1 确定 a：a 是只有一位整数的数； 2 确定 n：当原数的绝对值 1香 时，n 为正整数，n 等于原数的整数位数减 1；当原数的绝对值 1时，n 为负整数，n 的绝对值等于原数中左起第一个非零数前零的个数 含整数位数上的零 ． 3.答案：B 解析：解：A、 2 2ܽ ܽ 2 ܽ 2 ，故本选项正确，不符合题意； B、 2 7 ，故本选项错误，符合题意； C、 ܽ ܽ ，故本选项正确，不符合题意； D、 ܽ 2 2 ܽ 2 ，故本选项正确，不符合题意； 故选：B． 根据完全平方公式判断 A；根据同底数幂的乘法法则判断 B；根据去括号法则判断 C；根据单项式除 以单项式法则判断 D． 本题考查了完全平方公式、同底数幂的乘法、去括号法则、单项式除以单项式，掌握运算法则是解 题的关键． 4.答案：B 解析：解：如图， ሻ ， ሻ 9香 ． ܾ ， ܾሻ 9香 ． ሻܾ ， ሻ ܾሻ ． 故选：B． 由平行线的性质和余角的定义解答． 本题考查了平行线的性质和垂线，正确观察图形，熟练掌握平行线的性质和垂直的定义． 5.答案：D 解析： 本题考查了三视图的知识，俯视图是从物体的上面看得到的视图． 根据俯视图是从上面看到的图形结合几何体判定则可． 解：从上面看，左边是 2 个正方形，中间和右上角都是 1 个正方形． 故选：D． 6.答案：B 解析： 本题主要考查用坐标描述位置，点的坐标的确定，解不等式组及在数轴上表示不等式组的解集，可 根据第四象限的点的特征 列不等式组，解不等式组即可求解 m 的取值范围，再在数轴上表示 出来即可． 解： 点 2ʹ 11 ʹ 在第四象限， 2ʹ 1 香 1 ʹ 香 ， 解得 ʹ 1 2 ʹ 1 ， 将解集在数轴上表示为 ， 故选 B． 7.答案：B 解析： 本题考查了由实际问题抽象出二元一次方程组，解题关键是弄清题意，合适的等量关系，列出方程 组． 设有 x 匹大马，y 匹小马，根据 100 匹马恰好拉了 100 片瓦，已知一匹大马能拉 3 片瓦，3 匹小马能 拉 1 片瓦，列方程组即可． 解：设有 x 匹大马，y 匹小马，根据题意得 1香香 1 1香香 ． 故选 B． 8.答案：D 解析：解：A、“买中奖率为 1 1香 的奖券 10 张，中奖”是随机事件，故本选项错误； B、汽车累积行驶 10000km，从未出现故障”是随机事件，故本选项错误； C、襄阳气象局预报说“明天的降水概率为 7香ࣃ ”，意味着明天可能下雨，故本选项错误； D、若两组数据的平均数相同，则方差小的更稳定，故本选项正确； 故选：D． 根据随机时间的概念、概率的意义和方差的意义分别对每一项进行分析，即可得出答案． 此题考查了随机事件、概率的意义和方差的意义，正确理解概率的意义是解题的关键． 9.答案：C 解析：解： ሻ ， 72 ， ሻ 72 ， ܾ 垂直平分 AB， ሻܾ 䁜 ， ሻܾ ሻܾ 䁜 䁜 72 ． 故选 C． 先根据 ሻ ， 的度数，再由垂直平分线的性质求出 ሻܾ 的度数，再由三角形内角与外角的 性质解答即可． 本题考查的是线段垂直平分线的性质及三角形内角和定理、等腰三角形的性质，解答此题的关键是 熟知线段垂直平分线的性质，即线段的垂直平分线上的点到线段的两个端点的距离相等． 10.答案：B 解析： 此题主要考查圆内接四边形的性质，勾股定理 . 首先根据圆内接四边形的性质求出 ܾ 9香 ，然后 根据勾股定理即可求出 的半径长． 解：连接 AC， 四边形 ABCD 内接于 ， ሻ 9香 ， 是 的直径， ܾ 9香 ， ܾ 1香 ， ܾ ， ܾ 2 ܾ 2 1香 2 2 ， 的半径长为 2 ， 故选 B． 11.答案： 解析：解： 方程 2 香 有两个不相等的实数根， 香 ，即 2 香 ， 解得 ， 故答案为： ． 方程有两个不相等的实数根，则 香 ，建立关于 k 的不等式，求出 k 的取值范围． 本题考查根的判别式，总结：一元二次方程根的情况与判别式 的关系： 1 香 方程有两个不 相等的实数根； 2 香 方程有两个相等的实数根； 香 方程没有实数根． 12.答案： 1香 解析： 此题考查有理数的混合运算，理解规定的运算方法是解决问题的关键． 按照规定的运算，转化为有理数的混合运算计算即可． 解： 2 െ 12 2 1香 ． 故答案为： 1香 ． 13.答案： 1 解析： 首先根据题意画出树状图，然后由树状图求得所有等可能的结果与任选两个数的积作为 k 的值，使 反比例函数 的图象在第一、三象限的情况，再利用概率公式即可求得答案．本题考查的是用列 表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法 适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．注意概率 所求情况数与总情 况数之比． 解：画树状图得： 共有 6 种等可能的结果，任选两个数的积作为 k 的值，使反比例函数 的图象在第一、三象限 的有 2 种情况， 任选两个数的积作为 k 的值，使反比例函数 的图象在第一、三象限的概率是： 2 䁜 1 ． 故答案为 1 ． 14.答案： 2 解析：解： 2 向上平移 3 个单位长度， 新抛物线为 2 ． 故答案是： 2 ． 直接运用平移规律“左加右减，上加下减”，在原式上加 3 即可得新函数解析式 2 ． 主要考查了函数图象的平移，要求熟练掌握平移的规律：左加右减，上加下减．并用规律求函数解 析式． 15.答案： 解析： 本题考查了旋转的性质以及扇形的面积公式，全等三角形的性质，正确理解：阴影部分的面积 扇 形 OAB 的面积 扇形 OCD 的面积是解题关键．根据旋转的性质可以得到阴影部分的面积 扇形 OAB 的面积 扇形 OCD 的面积，利用扇形的面积公式即可求解． 解：由题意可得： ≌ ሻܾ ， 阴影部分的面积 扇形 OAB 的面积 扇形 OCD 的面积 12香 2 䁜香 12香1 2 䁜香 ， 故答案为 ． 16.答案： 䁜 1香 解析：解： 四边形 ABCD 是矩形， ܾ ሻ ， ܾ ሻ 䁜 ， ሻܾ ܾ 9香 ， ሻܾ ， ሻ ܾ ， 是边 CD 的中点， ܾ 1 2 ܾ 2 ， ܾ 2 ܾ 2 䁜 2 2 2 2 1香 ， ሻ ， ሻ 9香 ܾ ， ሻ∽ ܾ ， ሻ ሻ ܾ ， 即 2 1香 ሻ 䁜 ， 解得： ሻ 䁜 1香 ， 故答案为： 䁜 1香 ． 先根据矩形的性质得到 ܾ ሻ ， ܾ ሻ 䁜 ， ሻܾ ܾ 9香 ，求得 ܾ 2 ，再根据勾 股定理得到 2 1香 ，然后证明 ሻ∽ ܾ ，列比例式即可解得答案． 本题考查了相似三角形的判定和性质，勾股定理，矩形的性质等知识；熟练掌握相似三角形的判定 和性质是解题的关键． 17.答案：解： 2ܽ 2 ܽ ܽ 2 ܽ ܽ 2 ܽ ܽ 2 2 ܽ 2 2 2 䁜ܽ 2ܽ 䁜ܽ 2 ܽ ܽ 2 当 1 ， ܽ 时，原式 1 2 27 香 ． 解析：本题考查了整式的混合运算和求值，能正确根据整式的运算法则进行化简是解此题的关键 . 先 算乘法，再合并同类项，最后代入求出即可． 18.答案：18 解析：解： Ⅰ 一班人数所占比例为 1 2香ࣃ 2香ࣃ 2香ࣃ 香ࣃ ， 一班人数为 香ࣃ 1 人， 故答案为：18； Ⅱ 9 出现了 15 次，次数最多， 众数为 9； 共有 45 个数据，其中位数是第 23 个数据， 中位数是 10， 平均数为 911香1211912䁜 1香 ； Ⅲ 估计该校九年级一周课外阅读时间大于 10h 的约有 1香 9䁜 䁜香 人． Ⅰ 由百分比之和为 1 求得一班百分比，再用总人数乘以所得百分比即可得； Ⅱ 根据众数、中位数和平均数的定义求解； Ⅲ 用总人数乘以样本中阅读时间大于 10h 的人所占比例即可得． 本题考查的是扇形统计图与条形统计图的综合运用，涉及到众数、中位数和平均数的求法．读懂统 计图，从不同的统计图中得到必要的信息是解决问题的关键． 19.答案：解：设小汽车原来的平均速度为 x 千米 时，则现在走高速公路的平均速度是 1. 千米 时， 根据题意，得 1香 1香香 1. 1 1 䁜 ， 解这个方程，得 䁜香 ． 经检验 䁜香 是所列方程的解，这时 1. 1. 䁜香 9香 且符合题意． 答：小汽车原来的平均速度是 60 千米 时，走高速公路的平均速度是 90 千米 时． 解析：此题主要考查了分式方程的应用，关键是首先弄清题意，找出题目中的等量关系，设出未知 数列出方程，此题用到的公式是：行驶时间 路程 速度． 首先设小汽车原来的平均速度为 x 千米 时，则现在走高速公路的平均速度是 1. 千米 时，由题意 可得等量关系：原来从遂宁到内江走高速公路所用的时间 现在从遂宁到内江走高速公路所用的时 间 1 小时 10 分钟，根据等量关系列出方程，解方程即可． 20.答案：解：过点 N 作 交 AB 于点 E，交 CD 于点 F， 则 1.䁜 ， ， ሻ ܾ 9香 ， ， ， 则 ܾ ܾ 1䁜.䁜 1.䁜 1ʹ ， 在 ܾ 中， ܾ ， ܾ 1 ， 1 2香ʹ ， 在 ሻ 中， tanሻ ሻ ， ሻ tanሻ 2香 2香 1. 2.䁜ʹ ， ሻ ሻ 2.䁜 1.䁜 香ʹ ． 答：居民楼 AB 的高度约为 30 米． 解析：本题考查了解直角三角形的应用 仰角俯角问题，解决本题的关键是掌握仰角俯角定义．过 点 N 作 交 AB 于点 E，交 CD 于点 F，可得 1.䁜 ， ，再根据 锐角三角函数可得 BE 的长，进而可得 AB 的高度． 21.答案：解： 1 把 ʹ䁜 ， ሻ 两点分别代入 2 得 䁜 2ʹ ， 2 ， 解得 ʹ 1 ， 2 ， 点坐标为 1䁜 ，B 点坐标为 2 ， 把 1䁜 代入 求得 1 䁜 䁜 ， 反比例函数解析式为 䁜 ； 2 不等式 2 香 的解集为 1 ． 解析：本题考查了反比例函数与一次函数的交点问题：反比例函数与一次函数图象的交点坐标满足 两函数的解析式．也考查了待定系数法求函数的解析式以及观察图象的能力． 1 把 ʹ䁜 ， ሻ 两点分别代入 2 可求出 m、n 的值，确定 A 点坐标为 1䁜 ，B 点坐 标为 2 ，然后利用待定系数法求反比例函数的解析式； 2 观察函数图象得到当 1 ，一次函数的图象在反比例函数的图象上方． 22.答案： 1 证明：连接 OE， 则 ሻ 2ሻܾ ，又 2ሻܾ ， ሻ ， ሻܾ ， ሻ ， ሻܾ∽ ܾሻ ， 又 ሻ 是直径， ܾሻ 9香 与 相切； 2 解：连接 EB，则 ሻܾ ， ሻ ， ሻܾ ሻ ， 在 ሻ 和 ሻ 中， ሻ ሻ ， ሻ ሻ ， ሻ∽ ሻ ， ሻ ሻ ，则 ሻ ሻ ሻ ሻ ， ሻ ， ሻ ， ሻ ሻ ， ሻ 2 ， 1 ， 1 ሻ 2 1 ， ሻ 1 2 ． 解析：本题考查了切线的判定和性质以及相似三角形的判定与性质，正确的作出辅助线是解题的关 键． 1 连接 OE，首先得出 ሻܾ∽ ，进而推出 9香 ，即可得到结论； 2 连接 BE，得出 ሻ∽ ሻ ，再利用相似三角形的性质得出 OB 的长，即可得到结论． 23.答案：解 1 当 香 2香 时，设 1 ܽ1 ，由图象得 ܽ1 1䁜 2香1 ܽ1 2 解得 1 ܽ1 1䁜 1䁜 ； 当 2香 香 时，设 2 ܽ2 ，由图象得 2香2 ܽ2 2 香2 ܽ2 22 解得 2 1 ܽ2 2 1 2 ． 综上， 1䁜香 2香 1 22香 香 ， 2 由题意可得： 䁜香香 1䁜香香香香 ． 当 香 2香 时， 1香香香香 1䁜 䁜香香 1䁜香香香香 香香 香香 香 当 2香 时， 最大 香香 2香 1香香香香 ． 当 2香 香 时， 1 21香香 香香香 䁜香香 1䁜香香香香 2香 2 1香香香 9䁜香香香 2香 2 2 1香香香 2香 香 ，抛物线的开口向下， 当 2 时， 最大 1香香香 ． 1香香香 1香香香香 ， 当 2 时，W 取得最大值，该最大值为 108500 元． 解析： 1 根据图象，分类讨论利用待定系数法求出 y 与 t 的解析式即可； 2 表示出 W 与 t 的函数解析式，利用一次函数与二次函数的性质求出所求即可． 此题考查了二次函数的应用，待定系数法确定函数解析式，熟练掌握二次函数的性质是解本题的关 键． 24.答案：解： 1 连接 DE，如图， 点 O 是 ሻ 的重心， ܾ ，BE 是 BC，AC 边上的中线， ܾ ，E 为 BC，AC 边上的中点， ܾ 为 ሻ 的中位线， ܾሻ ， ܾ 1 2 ሻ ， ܾ∽ ሻ ， ܾ ܾ ሻ 1 2 ， ሻ 2 ， ሻܾ 1 ， ܾሻ 9香 ， ܾ ， ܾ ， ሻ ሻܾ 2 2 2 ， ሻ ሻܾ 2 2 2 ； 2 由 1 可知， ܾ 1 2 ，是定值； 点 O 到 BC 的距离和点 A 到 BC 的距离之比为 1：3， 则 ሻ 和 ሻ 的面积之比等于点 O 到 BC 的距离和点 A 到 BC 的距离之比， 故 ሻ ሻ 1 ，是定值； 四边形 ABCD 是正方形， ܾሻ ， ሻ ሻ ܾ ， ～ ሻ ， ሻ ሻ ， 为 CD 的中点， 1 2 ܾ 2 ， ሻ ሻ 2 2 2 ， ሻ 1 2 ， ሻ 1 ， 即 2 ； 1 ，且 ሻ 1 2 ， ሻ 2 ， ሻ 1 2 ， ሻ ሻ 2 1 ， ሻ ， ሻ ሻ ሻ 2 䁜 ， 又 ܾ ሻ ， ܾ 䁜 ， 正方形 ABCD 的面积为： 䁜 䁜 12 ． 解析： 1 连接 DE，利用相似三角形证明 ܾ 1 2 ，运用勾股定理求出 AD 的长，运用三角形面积公式 求解即可； 2 根据 1 的证明可求解； 证明 ∽ ሻ ，得 ሻ 1 2 ，再运用勾股定理求出 BE 的长即可解决问题； 分别求出 ሻ 和 ሻ 即可求得正方形 ABCD 的面积． 本题是一道相似形综合题目，主要考查的是三角形重心的性质、全等三角形的判定与性质、勾股定 理及相似三角形的判定与性质，解答此题的关键是明确题意，找出所求问题需要的条件，利用数形 结合的思想解答． 25.答案：解： 1 抛物线 2 ܽ 经过 香 ， ሻ1香 两点， 9 ܽ 香 ܽ 香 解得 1 ܽ 2 抛物线解析式为 2 2 1 2 ， 抛物线的顶点坐标为 1 ， 即该抛物线的解析式为 2 2 ，顶点 D 的坐标为 1 ； 2 设直线 AD 的函数解析式为 ʹ ， ʹ 香 ʹ 解得 2 ʹ 䁜 直线 AD 的函数解析式为 2 䁜 ， 点 P 是线段 AD 上一个动点 不与 A，D 重合 ， 设点 P 的坐标为 ݌2݌ 䁜 ， ݌2݌䁜 2 ݌ 2 2 9 ， ݌ 1 ， 当 ݌ 2 时， 取得最大值，此时 9 ， 即 面积 S 的最大值是 9 ； 抛物线上存在一点 Q，使得四边形 OAPQ 为平行四边形， 四边形 OAPQ 为平行四边形，点 Q 在抛物线上， ， 点 香 ， ， ， 直线 AD 为 2 䁜 ，点 P 在线段 AD 上，点 Q 在抛物线 2 2 上， 设点 P 的坐标为 ݌2݌ 䁜 ，点 2 2 ， ݌ 2݌ 䁜 2 2 ， 解得 ݌ 7 2 7 或 ݌ 7 2 7 舍去 ， 当 2 7 时， 2 2 2 7 ， 即点 Q 的坐标为 2 72 7 ． 解析：本题是一道二次函数综合题，解答本题的关键是明确题意，找出所求问题需要的条件，求出 相应的函数解析式，利用二次函数的性质和数形结合的思想解答． 1 根据抛物线 2 ܽ 经过 香 ， ሻ1香 两点，可以求得该抛物线的解析式，然后将 函数解析式化为顶点式，从而可以得到该抛物线的顶点坐标，即点 D 的坐标； 2 根据题意和点 A 和点 D 的坐标可以得到直线 AD 的函数解析式，从而可以设出点 P 的坐标，然后 根据图形可以得到 的面积，然后根据二次函数的性质即可得到 面积 S 的最大值； 根据题意可知存在点 Q 使得四边形 OAPQ 为平行四边形，然后根据函数解析式和平行四边形的 性质可以求得点 Q 的坐标．