2012年山东省菏泽市中考数学真题 9页

菏泽市二○一二年初中学业水平考试 数 学 试 题 注意事项： 1.本试题分选择题和非选择题两部分，其中选择题 24 分，非选择题 96 分，满分 120 分．考试时间 120 分钟． 2.用黑色、蓝色水笔或圆珠笔答卷，答卷前将密封线内的项目填写清楚． 3.请将选择题的正确答案代号（ABCD）填写在相应的“答题栏”内，将非选择题的答案 直接答在试卷上． 第Ⅰ卷（选择题 共 24 分） 一、选择题：本大题共 8 个小题，每小题 3 分，共 24 分．在每小题给出的四个选项 A、 B、C、D 中，只有一项是正确的，请把正确的选项选出来并填在第 3 页该题的相应的答题栏 内. 1.点 ( 21)P  ， 在平面直角坐标系中所在的象限是 （ ） A．第一象限 B．第二象限 C．第三象限 D．第四象限 2．在算式 33( ) ( )33的 中填上运算符号，使结果最大，这个运算符号是（ ） A．加号 B．减号 C．乘号 D．除号 3.如果用□表示 1 个立方体，用 表示两个立方体叠加，用■表示三个立方体叠加，那 么下面右图由 7 个立方体叠成的几何体，从正前方观察，则画出的平面示意图形是 ( ) 4．已知      1 2 y x 是二元一次方程组      1 8 mynx nymx 的解，则 nm 2 的算术平方根为（ ） A．±2 B． 2 C．2 D． 4 5.下列图形中是中心对称图形的是 （ ） A B C D A. B. C. D. 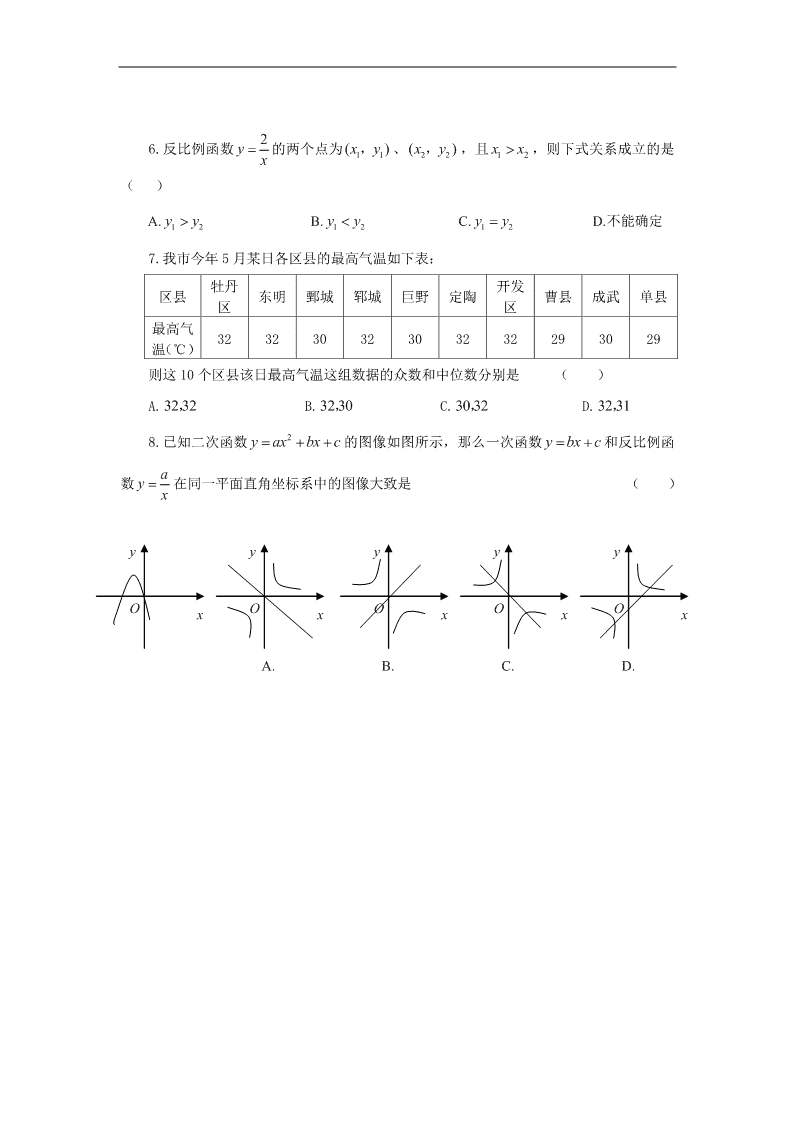6.反比例函数 2y x 的两个点为 11()xy， 、 22()xy， ，且 12xx ，则下式关系成立的是 （ ） A. 12yy B. 12yy C. 12yy D.不能确定 7.我市今年 5 月某日各区县的最高气温如下表： 区县 牡丹 区 东明 鄄城 郓城 巨野 定陶 开发 区 曹县 成武 单县 最高气 温（ ℃） 32 32 30 32 30 32 32 29 30 29 则这 10 个区县该日最高气温这组数据的众数和中位数分别是 （ ） A.32 32， B.32 30， C.30 32， D.32 31， 8.已知二次函数 2y ax bx c   的图像如图所示，那么一次函数 y bx c和反比例函 数 ay x 在同一平面直角坐标系中的图像大致是 （ ） x y O x y O x y O x y O x y O A. B. C. D. 32 3 5 7 33 9 11 34 13 15 17 19 第Ⅱ卷（非选择题 共 96 分） 二、填空题：本大题共 6 个小题，每小题 3 分，共 18 分，只要求填写最后结果，每小 题填对得 3 分. 9. 已 知 线 段 8cmAB  ， 在 直 线 AB 上 画 线 段 BC , 使 =3cmBC ， 则 线 段 AC  ________ . 10.若不等式组 3x xm    的解集是 3x  ，则 m 的取值范围是 . 11. 如图，PA，PB 是⊙O 的切线，A，B 为切点， AC 是 ⊙O 的直径，若∠P =46°，则∠BAC = 度. 12.口袋内装有大小、质量和材质都相同的红色 1 号、红色 2 号、黄色 1 号、黄色 2 号、 黄色 3 号的 5 个小球，从中摸出两球，这两球都是红色的概率是 . 13.将 4 个数 a b c d， ， ， 排成 2 行、2 列，两边各加一条竖直线记成 ab cd ，定义 ab cd ad bc，上述记号就叫做二阶行列式．若 1 1 81 1 xx xx  ，则 x  ． 14、一个自然数的立方，可以分裂成若干个连续奇数的和．例如： 32 ， 33 和 34 分别可 以按如图所示的方式“分裂”成 2 个、3 个和 4 个连续奇数的和，即 32 3 5； 33 7 9 11   ； 34 13 15 17 19    ； ……；若 36 也按照此规律来进行“分裂”， 则 36 “分裂”出的奇数中，最大的那个奇数是 ． 三、解答题：本大题共 7 个小题，共 78 分．解答应写出必要的文字说明、证明过程或 演算步骤． 15.（本题 12 分，每题 6 分） （1）先化简，再求代数式的值． 2 22() 111 aa aaa   ，其中 2012( 1) tan60a    ． （11 题图） （2）解方程：( 1)( 1) 2( 3) 8x x x     . 16. （本题 12 分，每题 6 分） （1）如图，∠DAB＝∠CAE，请你再补充一个条件： ________ ， 使△ABC∽△ADE，并说明理由． A B C D E （2）如图，OABC 是一张放在平面直角坐标系中的矩形纸片，O 为原点，点 A 在 x 轴 的正半轴上，点C 在 y 轴的正半轴上， 10 8OA OC， ．在 OC 边上取一点 D ，将纸片沿 AD 翻折，使点O 落在 BC 边上的点 E 处，求 DE， 两点的坐标. 17.（本题 14 分，每题 7 分） （1）如图，一次函数 2y= 23 x的图像分别与 x 轴、y 轴交于点 A 、B ，以线段 AB 为 边在第一象限内作等腰 Rt ABC , 90BAC .求过 、C 两点直线的解析式. x y O A B C （2）我市某校为了创建书香校园，去年购进一批图书.经了解，科普书的单价比文学书 的单价多 4 元，用 12000 元购进的科普书与用 8000 元购进的文学书本数相等.今年文学书和 科普书的单价和去年相比保持不变，该校打算用 10000 元再购进一批文学书和科普书，问购 进文学书 550 本后至多还能购进多少本科普书？ 18.（本题 10 分）如图，在边长为 1 的小正方形组成的网格中，△ ABC 和△ DEF 的顶 点都在格点上，P1，P2，P3，P4，P5 是△ DEF 边上的 5 个格点，请按要求完成下列各题： （1）试证明△ ABC 为直角三角形； （2）判断△ ABC 和△ DEF 是否相似，并说明理由； （3）画一个三角形，使它的三个顶点为 P1，P2，P3，P4，P5 中的 3 个格点并且与△ ABC 相似(要求：用尺规作图，保留痕迹，不写作法与证明)． A C B F E D P1 P2 P3 P4 P5 19.（本题 10 分）某中学举行数学知识竞赛，所有参赛学生分别设有一、二、三等奖和 纪念奖，获奖情况已绘制成如图所示的两幅不完整的统计图.根据图中所给出的信息解答下 列问题： （1）二等奖所占的比例是多少？ （2）这次数学知识竞赛获得二等奖的人数是多少？ （3）请将条形统计图补充完整； （4）若给所有参赛学生每人发一张卡片，各自写上自己的名字，然后把卡片放入一个 不透明的袋子里，摇匀后任意摸取一张卡片，求摸出的卡片上是写有一等奖学生名字的概率. 一等奖 10% 二等奖 三等奖 24% 纪念奖 46% 人数（人） 20 40 60 80 100 0 20.（本题 10 分） 2012 年牡丹花会前夕，我市某工艺厂设计了一款成本为 10 元/件的工艺品投放市场进行 试销．经过调查，得到如下数据： （1）把上表中 x 、 y 的各组对应值作为点的坐标，在下面的平面直角坐标系中描出相 应的点，猜想 与 的函数关系，并求出函数关系式； （2）当销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？最大利润是 多少？（利润=销售总价-成本总价） （3）菏泽市物价部门规定，该工艺品销售单价最高不能．．超过 35 元/件，那么销售单价 销售单价 （元∕件）…… 20 30 40 50 60 …… 每天销售量 （件）…… 500 400 300 200 100 …… 定为多少时，工艺厂试销该工艺品每天获得的利润最大？ 21. （本题 10 分） 如图，在平面直角坐标系中放置一直角三角板，其顶点为 (01) (2 0) (0 0)A B O，， ，， ， ,将此 三角板绕原点O 逆时针旋转90 ，得到 ABO . （1）一抛物线经过点 A 、 B 、 B ，求该抛物线的解析式； （2）设点 P 是在第一象限内抛物线上的一动点，是否存在点 ，使四边形 PB A B 的面 积是 ABO 面积的 4 倍？若存在，请求出点 P 的坐标；若不存在，请说明理由. （3）在（2）的条件下，试指出四边形 是哪种形状的四边形？并它的两条性质. x y O -1 1 2 2 1 A B A B