- 453.63 KB
- 2021-11-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
数学随堂小练北师大版(2012)九年级下册
3.4 圆周角和圆心角的关系
一、单选题
1.下面四个图中的角,为圆心角的是( )
A. B.
C. D.
2.下列四个图中, x 为圆周角的是( )
A. B. C. D.
3.如图, » »,AB CD 是 Oe 的直径, » »AE BD ,若 32AOE ,则 COE 的度数是()
A.32 B. 60 C. 68 D. 64
4.如图,已知 ABC△ 内接于 Oe ,点 P 在 Oe 内,点 O 在 PAB△ 内,若 50C ,则 P 的度数可
以为( )
A.20° B.50° C.110° D.80°
5.如图,在三个等圆上各自有一条劣弧 » » », ,AB CD EF ,如果 » » »AB CD EF ,那么 AB CD 与 EF
的大小关系是( )
A. AB CD EF
B. AB CD EF
C. AB CD EF
D.不能确定
6.如图, ,C D 是以线段 AB 为直径的 O 上两点.若CA CD ,且 40ACD ,则 CAB ( )
A.10 B. 20 C.30 D. 40
7.如图,在 O 中, , 48 ,OA BC AOB D 为 O 上一点.若 90BCD ° ,则
1 的度数是( )
A. 66° B. 42° C. 48° D.56°
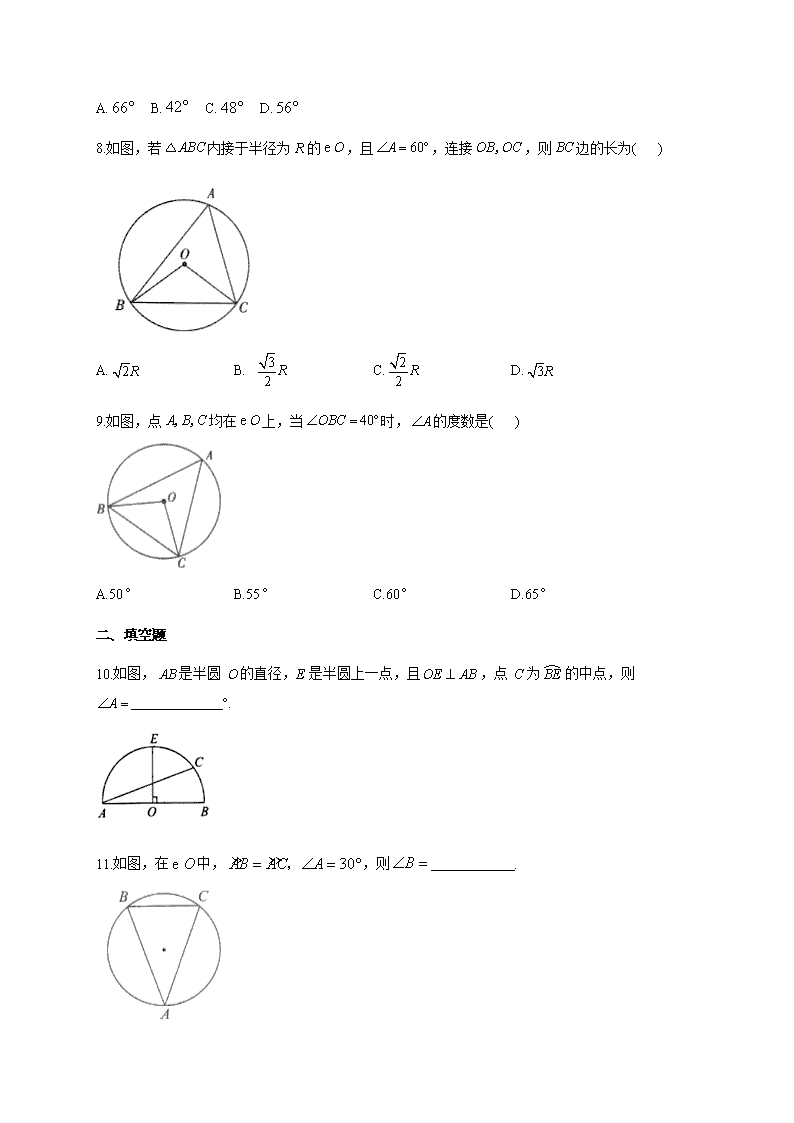
8.如图,若 ABC△ 内接于半径为 R 的 Oe ,且 60A ,连接OB OC, ,则 BC 边的长为( )
A. 2R B. 3
2 R C. 2
2 R D. 3R
9.如图,点 A B C, , 均在 Oe 上,当 40OBC 时, A 的度数是( )
A.50° B.55° C.60° D.65°
二、填空题
10.如图, AB 是半圆 O 的直径,E 是半圆上一点,且 OE AB ,点 C 为 BE 的中点,则
A °.
11.如图,在 Oe 中, » » 30AB AC A , ,则 B .
12.如图, AB CD EF, , 都是 Oe 的直径,且 1 2 3 ,则 Oe 的弦 AC BE DF, , 的大小关系
是 .
13.如图, CD 是 O 的直径,若 AB CD ,垂足为 , 40B OAB ° ,则 C 等于 度.
三、解答题
14.如图, O 的直径 4, 30AB ABC , BC 交 O 于点 ,D D 是 BC 的中点。
(1)求 BC 的长;
(2)过点 D 作 DE AC ,垂足为 ,E 求证:直线 DE 是 O 的切线.
参考答案
1.答案:D
Q 圆心角的顶点必须在圆心上,选项 A、B、C 均不正确.故选 D.
2.答案:C
根据圆周角的定义,只有选项 C 符合要求.
3.答案:D
» »AE BDQ , 32BOD AOE , BOD AOC Q , 32AOC ,
COE AOE AOC 32 32 64 .
4.答案:D
解:延长 AP 交圆 O 于 D,连接 BD ,
则 50ADB C ,
50APB ADB ,
Q 点 O 在 PAB△ 内,
90APB ,
P 的 度数可以为 80°,
故选:D.
5.答案:B
如图,在 EF 上取一点 M,使 ¼ »EM CD ,
则 ¼ »FM AB AB FM CD EM , ,
在 MEF△ 中, FM EM EF AB CD EF , 故选 B
6.答案:B
40 ,ACD CA CD
1 (180 40 ) 702CAD CDA
70ABC ADC
AB 是直径, 90ACB
90 20CAB B ,故选 B.
7.答案:A
, ,OA BC AC AB
1 1 48 242 2ADC AOB ° °
在 ECD△ 中, 1 180 90 24 66 ° ° ° ° .故选 A.
8.答案:D
如图,延长 BO 交 Oe 于点 D,连接 CD ,
易知 90BCD , 60D A , 30CBD
2BD RQ , DC R , 3BC R 故选 D
9.答案:A
OB OCQ , 40OCB OBC ,
180 40 40 100BOC ,
1 502A BOC .
10.答案:22.5
如图,连接 OC .
, 90 .OE AB EOB °
∵点 C 为 BE 的中点, 45BOC ° .
1 1 45 22.52 2A BOC ° ° .
11.答案:75
Q 在 Oe 中, » »AB AC , AB AC ,
ABC△ 是等腰三角形, B C
又 180 3030 752A B ,
12.答案: AC BE DF
1 2 3 1 2 3AOC BOE DOF Q , , ,且 ,
AOC BOE DOF AC BE DF .
13.答案:25
, 40 , 50 .AB CD OAB AOB ° °
C 与 AOB 分别为 AD 所对的圆周角和圆心角,
1 252C AOB °
14.答案:(1)如图,连接 AD .
AB 为 O 的直径, 90ADB .
又 30 , 4ABC AB , 2AD , 2 3BD .
D 为 BC 的中点, 2 4 3BC BD .
(2)证明:如图,连接 OD .
,D O 分别为 ,BC AB 的中点,
DO 是 ABC△ 的中位线, / /DO AC .
又 DE AC , DO DE ,
直线 DE 是 O 的切线.
相关文档
- 初中数学竞赛辅导讲义及习题解答 2021-11-107页
- 初中数学竞赛辅导讲义及习题解答 2021-11-109页
- 初中数学阴影部分面积计算模型大全2021-11-109页
- 初中数学竞赛辅导讲义及习题解答 2021-11-107页
- 人教版初中数学九年级下册课件第二2021-11-1022页
- 沪教版(上海)初中数学九年级第一学期2021-11-103页
- 2020人教版初中数学九年级上册知识2021-11-1036页
- 湘教版(2012)初中数学八年级下册 2平2021-11-102页
- 初中数学中考总复习课件PPT:第7课时2021-11-1011页
- 初中数学中考总复习课件PPT:19矩形2021-11-1019页