2009年山东省济南市中考数学试题及答案 13页

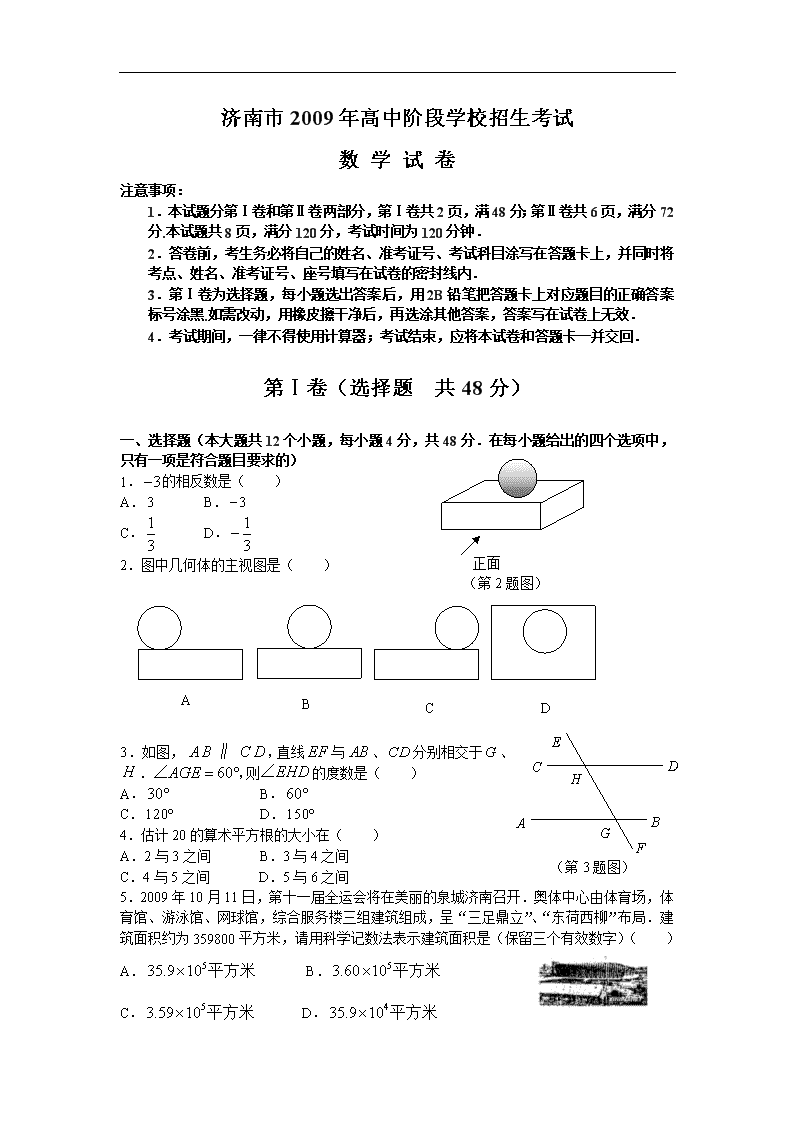
济南市 2009 年高中阶段学校招生考试 数 学 试 卷 注意事项： 1．本试题分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷共 2 页，满 48 分；第Ⅱ卷共 6 页，满分 72 分.本试题共 8 页，满分 120 分，考试时间为 120 分钟． 2．答卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上，并同时将 考点、姓名、准考证号、座号填写在试卷的密封线内． 3．第Ⅰ卷为选择题，每小题选出答案后，用 2B 铅笔把答题卡上对应题目的正确答案 标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案，答案写在试卷上无效． 4．考试期间，一律不得使用计算器；考试结束，应将本试卷和答题卡一并交回． 第Ⅰ卷（选择题　共 48 分） 一、选择题（本大题共 12 个小题，每小题 4 分，共 48 分．在每小题给出的四个选项中， 只有一项是符合题目要求的） 1． 的相反数是（ ） A． B． C． D． 2．图中几何体的主视图是（ ） 3．如图， 直线 与 、 分别相交于 、 ． 则 的度数是（ ） A． 　 B． C． 　　　 D． 4．估计 20 的算术平方根的大小在（ ） A．2 与 3 之间 　 B．3 与 4 之间 C．4 与 5 之间 D．5 与 6 之间 5．2009 年 10 月 11 日，第十一届全运会将在美丽的泉城济南召开．奥体中心由体育场，体 育馆、游泳馆、网球馆，综合服务楼三组建筑组成，呈“三足鼎立”、“东荷西柳”布局．建 筑面积约为 359800 平方米，请用科学记数法表示建筑面积是（保留三个有效数字）（ ） A． 　　 B． C． 　 　　D． 3− 3 3− 1 3 1 3 − A B C D∥ ， EF AB CD G H 60AGE = °∠ ， EHD∠ 30° 60° 120° 150° 535.9 10× 平方米 53.60 10× 平方米 53.59 10× 平方米 435.9 10× 平方米 A C E B F D H G （第 3 题图） 正面 （第 2 题图） A ． B ． C ． D ． 6．若 是一元二次方程 的两个根，则 的值是（ ） A． 　　　　B． 　　　　C． 　　　D． 7．“只要人人都献出一点爱，世界将变成 美好的人间”．在今年的慈善一日捐活动中， 济南市某中学八年级三班 50 名学生自发组织 献爱心捐款活动．班长将捐款情况进行了 统计，并绘制成了统计图．根据右图提供 的信息，捐款金额的众数和中位数分别是 （ ） A．20、20　 B．30、20 C．30、30　 D．20、30 8．不等式组 的解集在数轴上 表示正确的是（ ） 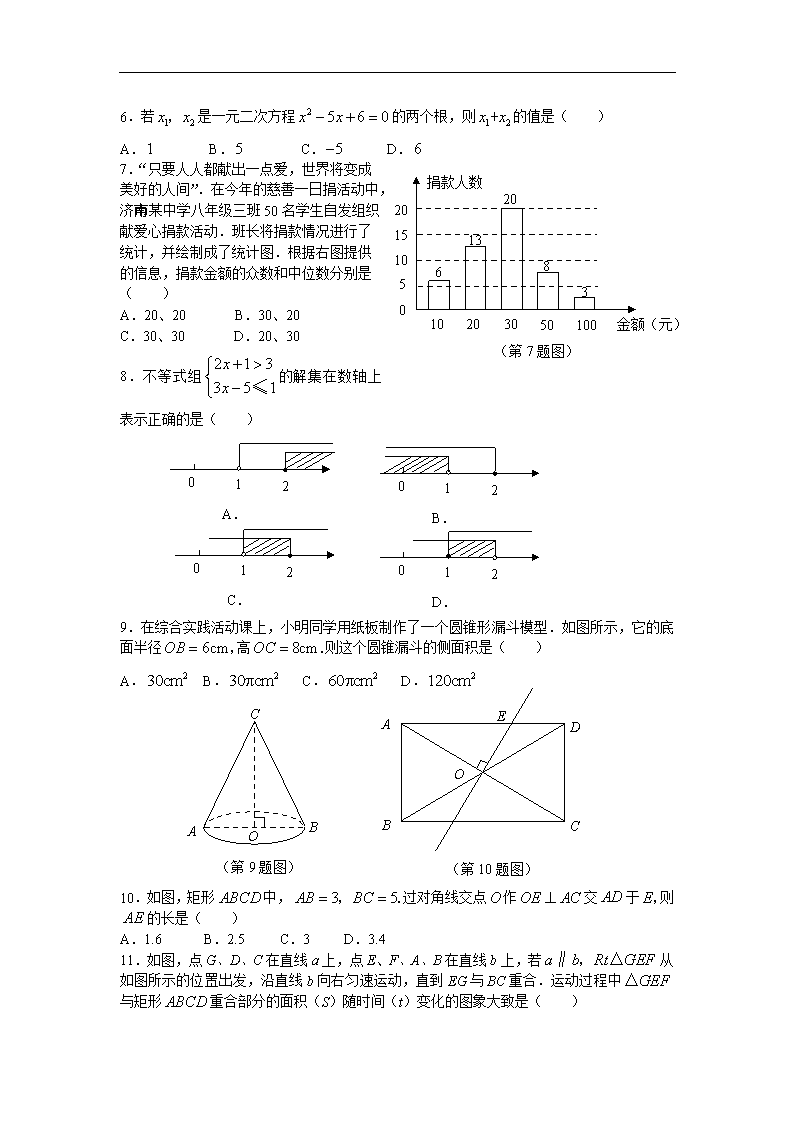9．在综合实践活动课上，小明同学用纸板制作了一个圆锥形漏斗模型．如图所示，它的底 面半径 高 则这个圆锥漏斗的侧面积是（ ） A． 　B． C． D． 10．如图，矩形 中， 过对角线交点 作 交 于 则 的长是（ ） A．1.6 B．2.5 C．3 D．3.4 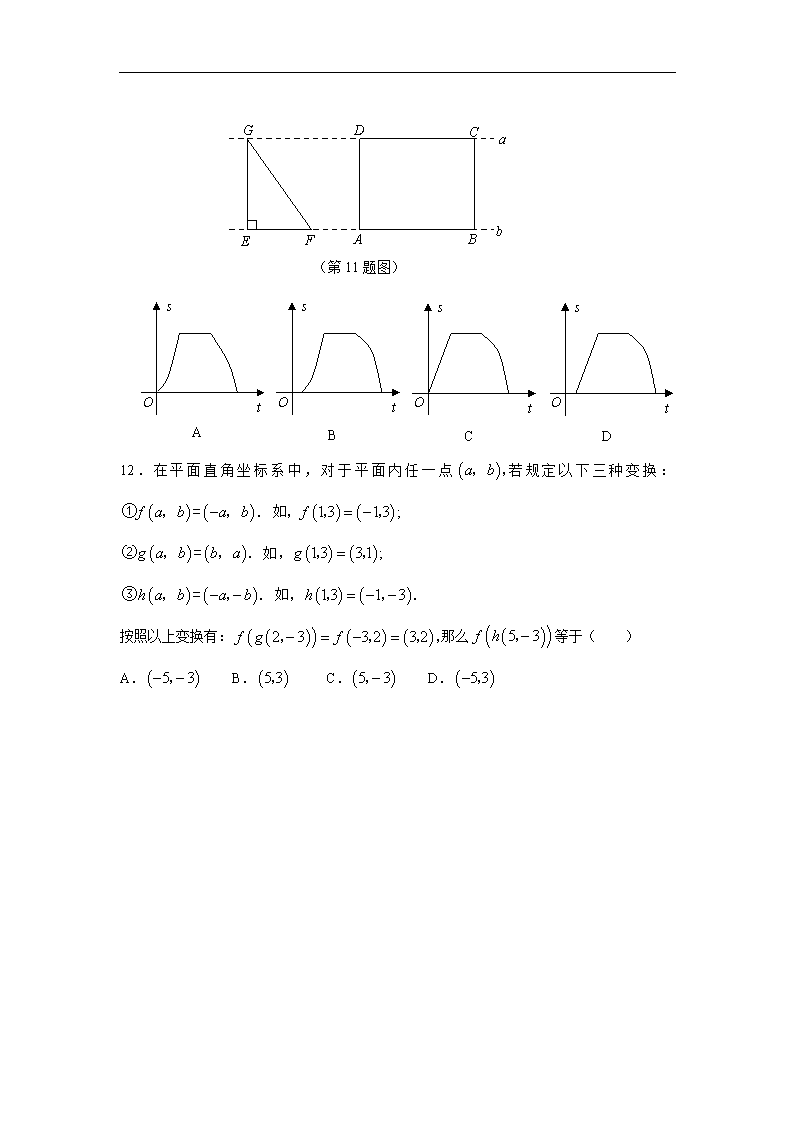11．如图，点 G、D、C 在直线 a 上，点 E、F、A、B 在直线 b 上，若 从 如图所示的位置出发，沿直线 b 向右匀速运动，直到 EG 与 BC 重合．运动过程中 与矩形 重合部分的面积（S）随时间（t）变化的图象大致是（ ） 1 2x x， 2 5 6 0x x− + = 1 2x x+ 1 5 5− 6 2 1 3 3 5 1 x x + >  − ≤ 6cmOB = ， 8cmOC = ． 230cm 230 cmπ 260 cmπ 2120cm ABCD 3 5AB BC= =， ． O OE AC⊥ AD E， AE a b Rt GEF∥ ， △ GEF△ ABCD 1 20 A． B． 1 20 C． 1 20 D． 1 20 （第 9 题图） BA C c O A B C D O E （第 10 题图） 捐款人数 金额（元） 0 5 10 15 20 6 1 13 1 20 8 3 20 30 50 100 （第 7 题图） 10 12 ． 在 平 面 直 角 坐 标 系 中 ， 对 于 平 面 内 任 一 点 若 规 定 以 下 三 种 变 换 ： 按照以上变换有： 那么 等于（ ） A． B． C． D． ( )a b， ， ( ) ( ) ( ) ( )13 13 ;f a b a b f− = −如① ， = ， ． ， ， ， ( ) ( ) ( ) ( )13 31 ;g a b b a g =如② ， = ， ． ， ， ， ( ) ( ) ( ) ( )13 1 3h a b a b h− − = − −如③ ， = ， ． ， ， ， ． ( ( )) ( ) ( )2 3 3 2 3 2f g f− = − =， ， ， ， ( )( )5 3f h −， ( )5 3− −， ( )5 3， ( )5 3−， ( )5 3− ， G D C E F A B b a （第 11 题图） s tO A ． s tO B ． C ． s tO D ． s tO 注意事项： 1.第Ⅱ卷共 6 页．用蓝、黑钢笔或圆珠笔直接答在考试卷上． 2.答卷前将密封线内的项目填写清楚．考试时间，一律不得使用计算器． 第Ⅱ卷（非选择题　共 72 分） 二、填空题（本大题共 5 个小题，每小题 3 分，共 15 分．把答案填在题中横线上） 13．分解因式： ． 14．如图， 的半径 弦 点 为弦 上一动点，则点 到圆心 的最短距离是 cm． 15．如图， 是放置在正方形网格中的一个角，则 的值是 ． 16．“五一”期间，我市某街道办事处举行了“迎全运，促和谐”中青年篮球友谊赛．获得 男子篮球冠军球队的五名主力队员的身高如下表：（单位：厘米） 号码 4 7 9 10 23 身高 178 180 182 181 179 则该队主力队员身高的方差是 厘米 2． 17．九年级三班小亮同学学习了“测量物体高度”一节课后，他 为了测得右图所放风筝的高度，进行了如下操作： （1）在放风筝的点 处安置测倾器，测得风筝 的仰角 ； （2）根据手中剩余线的长度出风筝线 的长度为 70 米； （3）量出测倾器的高度 米． 根据测量数据，计算出风筝的高度 约为 米．（精确 到 0.1 米， ） 三、解答题（本大题共 7 个小题，共 57 分.解答应写出文字说明、证明过程或演算步骤） 18．（本小题满分 7 分） （1）计算： （2）解分式方程： 19．（本小题满分 7 分） 2 9x − = O 5cmOA = ， 8cmAB = ， P AB P O AOB∠ cos AOB∠ A C 60CBD = °∠ BC 1.5AB = CE 3 1.73≈ ( ) ( )21 2 1x x+ + − 2 1 3 1x x =− − ． O A P B （第 14 题图） O A B （第 15 题图） A D B E C 60° （第 17 题图） （1）已知，如图①，在 中， 、 是对角线 上的两点，且 求证： （2）已知，如图②， 是 的直径， 与 相切于点 连接 交 于点 的延长线交 于点 连接 、 ， 求 和 的度数． 20．（本小题满分 8 分） 有 3 张不透明的卡片，除正面写有不同的数字外，其它均相同．将这三张卡片背面朝上洗匀 后，第一次从中随机抽取一张，并把这张卡片标有的数字记作一次函数表达式中的 ，第二 次从余下的两张卡片中再随机抽取一张，上面标有的数字记作一次函数表达式中的 （1）写出 为负数的概率； （2）求一次函数 的图象经过二、三、四象限的概率．（用树状图或列表法求解） ABCD E F BD BF DE= ． AE CF= ． AB O CA O A． CO O D， CO O E． BE BD 30ABD = °∠ ， EBO∠ C∠ k b． k y kx b= + A E C D F B （第 19 题图 ①） A C D B EO （第 19 题图②） 1− 2− 3− 正面 背面 21．（本小题满分 8 分） 自 2008 年爆发全球金融危机以来，部分企业受到了不同程度的影响，为落实“促民生、促 经济”政策，济南市某玻璃制品销售公司今年 1 月份调整了职工的月工资分配方案，调整后 月工资由基本保障工资和计件奖励工资两部分组成（计件奖励工资=销售每件的奖励金额× 销售的件数）．下表是甲、乙两位职工今年五月份的工资情况信息： 职工 甲 乙 月销售件数（件） 200 180 月工资（元） 1800 1700 （1）试求工资分配方案调整后职工的月基本保障工资和销售每件产品的奖励金额各多少 元？ （2）若职工丙今年六月份的工资不低于 2000 元，那么丙该月至少应销售多少件产品？ 22．（本小题满分 9 分） 已知：如图，正比例函数 的图象与反比例函数 的图象交于点 （1）试确定上述正比例函数和反比例函数的表达式； （2）根据图象回答，在第一象限内，当 取何值时，反比例函数的值大于正比例函数的值？ （3） 是反比例函数图象上的一动点，其中 过点 作直线 轴， 交 轴于点 ；过点 作直线 轴交 轴于点 ，交直线 于点 ．当四边形 的面积为 6 时，请判断线段 与 的大小关系，并说明理由． 23．（本小题满分 9 分） 如图，在梯形 中， 动点 从 点出发沿线段 以每秒 2 个单位长度的速度向终点 运动；动点 同时从 点出发 沿线段 以每秒 1 个单位长度的速度向终点 运动．设运动的时间为 秒． （1）求 的长． （2）当 时，求 的值． （3）试探究： 为何值时， 为等腰三角形． y ax= ky x = ( )3 2A ， ． x ( )M m n， 0 3m< < ， M MN x∥ y B A AC y∥ x C MB D OADM BM DM ABCD 3 5 4 2 45AD BC AD DC AB B= = = = °∥ ， ， ， ，∠ ． M B BC C N C CD D t BC MN AB∥ t t MNC△ A D CB M N （第 23 题图） （第 22 题图） y xO o A DM C B 24．（本小题满分 9 分） 已知：抛物线 的对称轴为 与 轴交于 两点，与 轴交 于点 其中 、 （1）求这条抛物线的函数表达式． （2）已知在对称轴上存在一点 P，使得 的周长最小．请求出点 P 的坐标． （3）若点 是线段 上的一个动点（不与点 O、点 C 重合）．过点 D 作 交 轴于点 连接 、 ．设 的长为 ， 的面积为 ．求 与 之间的函数 关系式．试说明 是否存在最大值，若存在，请求出最大值；若不存在，请说明理由． 济南市 2009 年高中阶段学校招生考试 数学试题参考答案及评分标准 一、选择题（本大题共 12 个小题，每小题 4 分，共 48 分） 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A B C C B B C C C D B B 二、填空题（本大题共 5 个小题，每小题 3 分，共 15 分） 13． 　14． 　15． 　16． 　17． 三、解答题（本大题共 7 个小题，共 57 分） 18．（本小题满分 7 分） （1）解： = ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分 = ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 ( )2 0y ax bx c a= + + ≠ 1x = − ， x A B， y C， ( )3 0A − ， ( )0 2C −， ． PBC△ D OC DE PC∥ x E． PD PE CD m PDE△ S S m S ( )( )3 3x x+ − 3 2 2 2 62.1 ( ) ( )21 2 1x x+ + − 2 2 1 2 2x x x+ + + − 2 3x + A C x y BO （第 24 题图） （2）解：去分母得： ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1 分 解得 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分 检验 是原方程的解 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 所以，原方程的解为 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 19．（本小题满分 7 分） （1）证明：∵四边形 是平行四边形， ∴ ∴ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1 分 在 和 中， ∵ ∴ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分 ∴ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 （2）解：∵ 是 的直径 ∴ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1 分 ∵ ∴ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分 ∵ 是 的切线 ∴ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 又 ∴ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 20．（本小题满分 8 分） 解：（1） 为负数的概率是 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 （2）画树状图 或用列表法： 第二次 第一次 （ ， ） （ ， ） （ ， ） （ ， ） （ ， ） （ ， ） ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5 分 ( )2 1 3x x− = − 1x = − 1x = − 1x = − ABCD AD BC AD BC= ， ∥ ． ADE FBC=∠ ∠ ADE△ CBF△ AD BC ADE FBC DE BF= = =，∠ ∠ ， ADE CBF△ ≌△ AE CF= DE O 90DBE = °∠ 30ABD = °∠ 90 30 60EBO DBE ABD= − = °− ° = °∠ ∠ ∠ AC O 90CAO = °∠ 2 60AOC ABD= = °∠ ∠ 180 180 60 90 30C AOC CAO= °− − = °− °− ° = °∠ ∠ ∠ k 2 3 1− 2− 3 1− 1− 2− 1− 3 2− 2− 1− 2− 3 3 3 1− 3 2− A E C D F B （第 19 题图 ①） A C D B EO （第 19 题图②） 2− 3 7 1− 3 2− 1 1− 2− 4 3 5 开始 第一次 第二次 共有 6 种情况，其中满足一次函数 经过第二、三、四象限， 即 的情况有 2 种 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 所以一次函数 经过第二、三、四象限的概率为 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 分 21．（本小题满分 8 分） 解：（1）设职工的月基本保障工资为 元，销售每件产品的奖励金额为 元∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1 分 由题意得 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 解这个方程组得 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 答：职工月基本保障工资为 800 元，销售每件产品的奖励金额 5 元.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5 分 （2）设该公司职工丙六月份生产 件产品∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 由题意得 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7 分 解这个不等式得 答：该公司职工丙六月至少生产 240 件产品∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 分 22．解：（1）将 分别代入 中，得 ∴ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分 ∴反比例函数的表达式为： ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 正比例函数的表达式为 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 （2）观察图象，得在第一象限内， 当 时，反比例函数的值大 于正比例函数的值． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 （3） ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7 分 理由：∵ ∴ 即 ∵ ∴ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 分 y kx b= + 0 0k b< <， y kx b= + 2 1 6 3 = x y 200 1800 180 1700 x y x y + =  + = 800 5 x y =  = z 800 5 2000z+ ≥ 240z≥ ( )3 2A ， ky y axx = =， 2 3 23 k a= =， 26 3k a= =， 6y x = 2 3y x= 0 3x< < BM DM= 1 32OMB OACS S k= = × =△ △ 3 3 6 12OMB OACOBDC OADMS S S S= + + = + + =△ △矩形 四边形 12OC OB = 3OC = 4OB = （第 22 题图） y xO o A DM C B 即 ∴ ∴ ∴ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9 分 23.（本小题满分 9 分） 解：（1）如图①，过 、 分别作 于 ， 于 ，则四边形 是矩形 ∴ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1 分 在 中， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分 在 中，由勾股定理得， ∴ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 （2）如图②，过 作 交 于 点，则四边形 是平行四边形 ∵ ∴ ∴ ∴ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 由题意知，当 、 运动到 秒时， ∵ ∴ 又 ∴ ∴ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5 分 即 解得， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 （3）分三种情况讨论： ①当 时，如图③，即 4n = 6 3 2m n = = 3 3 332 2 2MB MD= = − =， MB MD= A D AK BC⊥ K DH BC⊥ H ADHK 3KH AD= = ． Rt ABK△ 2sin 45 4 2 42AK AB= ° = = ． 2cos45 4 2 42BK AB= ° = =  Rt CDH△ 2 25 4 3HC = − = 4 3 3 10BC BK KH HC= + + = + + = D DG AB∥ BC G ADGB MN AB∥ MN DG∥ 3BG AD= = 10 3 7GC = − = M N t 10 2CN t CM t= = −， ． DG MN∥ NMC DGC=∠ ∠ C C=∠ ∠ MNC GDC△ ∽△ CN CM CD CG = 10 2 5 7 t t−= 50 17t = NC MC= 10 2t t= − （第 23 题图①） A D CB K H （第 23 题图②） A D CB G M N ∴ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7 分 ②当 时，如图④，过 作 于 解法一： 由等腰三角形三线合一性质得 在 中， 又在 中， ∴ 解得 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 分 解法二： ∵ ∴ ∴ 即 ∴ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 分 ③当 时，如图⑤，过 作 于 点. 解法一：（方法同②中解法一） 解得 解法二： ∵ ∴ ∴ 10 3t = MN NC= N NE MC⊥ E ( )1 1 10 2 52 2EC MC t t= = − = − Rt CEN△ 5cos EC tc NC t −= = Rt DHC△ 3cos 5 CHc CD = = 5 3 5 t t − = 25 8t = 90C C DHC NEC= ∠ = ∠ = °∠ ∠ ， NEC DHC△ ∽△ NC EC DC HC = 5 5 3 t t−= 25 8t = MN MC= M MF CN⊥ F 1 1 2 2FC NC t= = 1 32cos 10 2 5 tFCC MC t = = =− 60 17t = 90C C MFC DHC= ∠ = ∠ = °∠ ∠ ， MFC DHC△ ∽△ FC MC HC DC = A D CB M N （第 23 题图③） （第 23 题图④） A D CB M N H E （第 23 题图⑤） A D CB H N M F 即 ∴ 综上所述，当 、 或 时， 为等腰三角形∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9 分 24.（本小题满分 9 分） 解：（1）由题意得 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分 解得 ∴此抛物线的解析式为 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 （2）连结 、 .因为 的长度一定，所以 周长最小，就是使 最小. 点关于对称轴的对称点是 点， 与对称轴 的交点即为所求的 点 . 设直线 的表达式为 则 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 解得 ∴此直线的表达式为 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5 分 把 代入得 ∴ 点的坐标为 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 （3） 存在最大值 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7 分 1 10 22 3 5 t t−= 60 17t = 10 3t = 25 8t = 60 17t = MNC△ 12 9 3 0 2 b a a b c c  =  − + =   = − 2 3 4 3 2 a b c  =  =  = −  22 4 23 3y x x= + − AC BC BC PBC△ PC PB+ B A AC 1x = − P AC y kx b= + 3 0 2 k b b − + =  = − ， 2 3 2 k b  = −  = − 2 23y x= − − ． 1x = − 4 3y = − P 41 3  − −  ， S （第 24 题图） OA C x y B E P D 理由：∵ 即 ∴ ∴ 即 ∴ 方法一： 连结 = = ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 分 ∵ ∴当 时， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9 分 方法二： = = ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 分 ∵ ∴当 时， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9 分 DE PC∥ ， DE AC∥ ． OED OAC△ ∽△ ． OD OE OC OA = ， 2 2 3 m OE− = ． 3 33 32 2OE m AE OE m= − = =， ， OP OED POE POD OEDPDOES S S S S S= − = + −△ △ △ △四边形 ( ) ( )1 3 4 1 1 33 2 1 3 22 2 3 2 2 2m m m m   × − × + × − × − × − × −       23 3 4 2m m− + 3 04 − < 1m = 3 3 3 4 2 4S = − + =最大 OAC OED AEP PCDS S S S S= − − −△ △ △ △ ( )1 1 3 1 3 4 13 2 3 2 12 2 2 2 2 3 2m m m m × × − × − × − − × × − × ×   ( )223 3 3 314 2 4 4m m m− + = − − + 3 04 − < 1m = 3 4S =最大