北师大版九年级数学[上册]期末检测数学试题和答案解析[精品4套]+上册数学导学案 89页

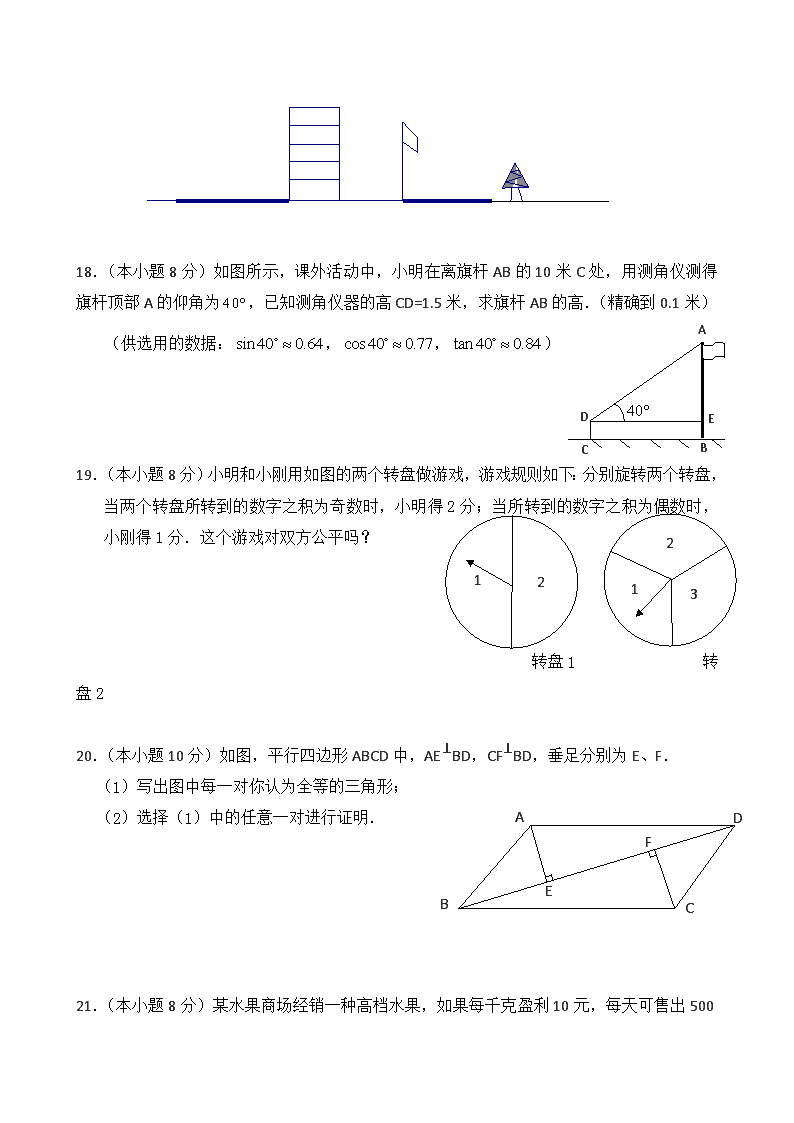
北师大版九年级数学[上册] 期末检测数学试题和答案解析[精品 4 套]+上册数学导学案 九年级数学上期末考试卷 一、选择题（本大题共 8 个小题，每题只有一个正确的选项，每小题 3分，满分 24 分） 1．一元二次方程 042 x 的解是（ ） A． 2x B． 2x C． 21 x ， 22 x D． 21 x ， 22 x 2．二次三项式 2 4 3x x  配方的结果是（ ） A． 2( 2) 7x   B． 2( 2) 1x   C． 2( 2) 7x   D． 2( 2) 1x   3．小明从上面观察下图所示的两个物体，看到的是（ ） A B C D 4．人离窗子越远，向外眺望时此人的盲区是（ ） A．变小 B．变大 C．不变 D．以上都有可能 5．函数 x ky  的图象经过（1，-1），则函数 2 kxy 的图象是（ ） 6．在 Rt△ABC 中，∠C=90°，a=4，b=3，则 sinA的值是（ ） A． 5 4 B． 3 5 C． 4 3 D． 4 5 7．下列性质中正方形具有而矩形没有的是（ ） A．对角线互相平分 B．对角线相等 正面 2 2 2 2 -2 -2 -2 -2O OOO y y y y xx x x A B C D C．对角线互相垂直 D．四个角都是直角 8．一只小狗在如图的方砖上走来走去，最终停在阴影方砖上的概率是（ ） A． 15 4 B． 3 1 C． 5 1 D． 15 2 二、填空题（本大题共 7 个小题，每小题 3分，满分 21 分） 9．计算 tan60°= ． 10．已知函数 2 2( 1) my m x   是反比例函数，则 m 的值为 ． 11．若反比例函数 x ky  的图象经过点（3，－4），则此函数在每一个象限内 y 随 x的增大而 ． 12．命题“直角三角形两条直角边的平方和等于斜边的平方”的逆命题是 ． 13．有两组扑克牌各三张，牌面数字分别为 2，3，4，随意从每组中牌中抽取一张，数字和 是 6的概率是 ． 14．依次连接矩形各边中点所得到的四边形是 ． 15．如图，在△ABC 中，BC = 8 cm，AB 的垂直平分线交 AB 于点Ｄ，交边 AC于点 E，△BCE 的周长等于 18 cm， 则 AC的长等于 cm． 三、解答题（本大题共 9个小题，满分 75分） 16．（本小题 6 分）解方程： 3 ( 3)x x x   17．（本小题 6分）如图，楼房和旗杆在路灯下的影子如图所示。试确定路灯灯炮的位置，再 作出小树在路灯下的影子．（不写作法，保留作图痕迹） 得 分 评卷人 得 分 评卷人 A D B C E 18．（本小题 8 分）如图所示，课外活动中，小明在离旗杆 AB 的 10 米 C 处，用测角仪测得 旗杆顶部 A 的仰角为 40，已知测角仪器的高 CD=1.5 米，求旗杆 AB 的高．（精确到 0.1 米） （供选用的数据： sin 40 0.64 ， cos 40 0.77 ， tan 40 0.84 ） 19．（本小题 8 分）小明和小刚用如图的两个转盘做游戏，游戏规则如下：分别旋转两个转盘， 当两个转盘所转到的数字之积为奇数时，小明得 2 分；当所转到的数字之积为偶数时， 小刚得 1分．这个游戏对双方公平吗？ 转盘 1 转 盘 2 20．（本小题 10分）如图，平行四边形 ABCD 中，AE⊥BD，CF⊥BD，垂足分别为 E、F． （1）写出图中每一对你认为全等的三角形； （2）选择（1）中的任意一对进行证明． 21．（本小题 8 分）某水果商场经销一种高档水果，如果每千克盈利 10 元，每天可售出 500 40 ED C B A 1 2 1 2 3 A B C D E F 千克，经市场调查发现，在进货价不变的情况下，出售价格每涨价 1元，日销售量将减少 20 千克，现该商场要保证每天盈利 6000元，同时又要使顾客得到实惠，那么每千克应涨价多少 元？ 22．（本小题 10 分）已知：如图，D 是△ABC 中 BC 边上一点，E 是 AD 上的一点， EB=EC， ∠1=∠2． 求证：AD平分∠BAC． 23．（本小题 9 分）正比例函数 kxy  和反比例函数 x ky  的图象相交于 A，B 两点，已知点 A 的横坐标为 1，纵坐标为3． （1）写出这两个函数的表达式； （2）求 B 点的坐标； （3）在同一坐标系中，画出这两个函数的图象． 24．（本小题 10分）阅读探索：“任意给定一个矩形 A，是否存在另一个矩形 B，它的周长和 21 A B C D E O 1 2 3 4 5 6 6 5 4 3 2 1 -1-2-3-4-5-6 -1 -2 -3 -4 -5 -6 x y 面积分别是已知矩形周长和面积的一半？”（完成下列空格） （1）当已知矩形 A 的边长分别为 6 和 1 时，小亮同学是这样研究的： 设所求矩形的两边分别是 yx和 ，由题意得方程组：       3 2 7 xy yx ， 消去 y 化简得： 0672 2  xx ， ∵△＝49－48>0，∴x1= ，x2= ． ∴满足要求的矩形 B 存在． （2）如果已知矩形 A 的边长分别为 2 和 1，请你仿照小亮的方法研究是否存在满足要求的矩 形 B． （3）如果矩形 A 的边长为 m 和 n，请你研究满足什么条件时，矩形 B 存在？ 九年级数学 参考答案 一、选择题 1．C 2．B 3．A 4．B 5．A 6．D 7．C 8．B 二、填空题 9． 3 10．-1 11．增大 12．如果三角形两边的平方和等于第三边的平方，那么这个三 角形是直角三角形 13． 1 3 14．菱形 15．10 三、解答题 16．（本小题 6分） 解方程得 x1=1，x2=3 17．（本小题 6分） 略 18．（本小题8分） 解：在 Rt△ADE 中， tan ADE= DE AE ∵ DE=10， ADE=40° ∴ AE=DE tan ADE =10 tan 40°≈10 0.84 =8.4 ∴ AB=AE+EB=AE+DC=8.4 1.5 9.9  答：旗杆 AB 的高为9.9米 19．解：∵P（奇数）= 3 1 P（偶数）= 3 2 ∵ 3 1 ×2= 3 2 ×1 ∴这个游戏对双方是公平的 20．解：（1）△ABD≌△CDB，△AEB≌△CFD，△AED≌△CFB（2）证明略 21．解：设每千克应涨价 x元，根据题意，得 (10 )(500 20 ) 6000x x   即 2 15 50 0x x   ， 解 得 x1=5，x2=10 ∵要使顾客得到实惠 ∴ 102 x 舍去 答：每千克应涨价 5 元。 22．（本小题 10分） 解：上面的证明过程不正确，错在第一步。 证明：∵EB=EC， ∴∠3=∠4 又∵∠1=∠2∴∠1+∠3=∠2+∠4 即∠ABC=∠ACB 转盘 2 转盘 1 1 2 3 1 1 2 3 2 2 4 6 21 A B CD E 3 4 ∴AB=AC∴在△AEB 和△AEC 中， EB=EC 1= 2 AB=AC      ∴△AEB≌△AEC ∴∠BAE=∠CAE∴AD 平分∠BAC 23．解：（1）∵正比例函数 y=kx与反比例函数 x ky  的图像都过点 A（1，3），则 k=3∴正比例函数是 y=3x ， 反比例函数是 3y x  （2）∵点 A 与点 B 关于原点对称，∴点 B 的坐标是（-1，-3）（3）略 24．解：（1）2 和 3 2 ；（2） 3 2 1 x y xy       ，消去 y 化简得：2 x2－3x＋2＝０，Δ＝9-16<０，所以不存在矩形 B． （3）（m + n）2 －8mn≥0， 设所求矩形的两边分别是 yx和 ，由题意得方程组： 2 2 m nx y mnxy        ，消去 y 化简得：2 x2－（m + n）x + mn = 0， Δ＝（m + n）2 －8mn≥0． 即（m + n）2－8mn≥0 时，满足要求的矩形 B 存在 九年级数学上学期期末检测试题卷 一、选择题（本大题共 8 个小题，每题只有一个正确的选项，每小题 3分，满分 24 分） 1．下列方程中，是一元二次方程的是（ ） A． 32  yx B． 2( 1) 3x   C． 113 22  xxx D． 2 9x  2．有一实物如下左图，那么它的主视图是（ ） 3．到三角形各顶点的距离相等的点是三角形（ ） A．三条角平分线的交点 B．三条高的交点 C．三边的垂直平分线的交点 D．三条中线的交点 A B C D 4．甲、乙两地相距 60km，则汽车由甲地行驶到乙地所用时间 y（小时）与行驶速度 x（千米/时）之间的 函数图像大致是（ ） 5．下列命题中，不正确的是（ ） A．顺次连结菱形各边中点所得的四边形是矩形 B．有一个角是直角的菱形是正方形 C．对角线相等且垂直的四边形是正方形 D．有一个角是 60°的等腰三角形是等边三角形 6．在 Rt△ABC 中，∠C=90°，a=4，b=3，则 sinA 的值是（ ） A． 4 5 B． 3 5 C． 4 3 D． 5 4 7．电影院呈阶梯或下坡形状的主要原因是( ) A．为了美观 B．减小盲区 C．增大盲区 D．盲区不变 8．某校九年级一班共有学生 50 人，现在对他们的生日（可以不同年）进行统计，则正确的说法是（ ） A．至少有两名学生生日相同 B．不可能有两名学生生日相同 C．可能有两名学生生日相同，但可能性不大 D．可能有两名学生生日相同，且可能性很大 二、填空题（本大题共 7 个小题，每小题 3分，满分 21 分） 9．计算 2cos60°+ tan245°= 。 10．一元二次方程 2 3 0x x  的解是 。 11．请你写出一个反比例函数的解析式使它的图象在第一、三象限 。 12．在平行四边形 ABCD 中，对角线 AC 长为 10 cm，∠CAB=30°，AB= 6 cm，则平行四边形 ABCD 的面积 为 2cm 。 13．命题“等腰梯形的对角线相等”。它的逆命题是 . 14．随机掷一枚均匀的硬币两次，至少有一次正面朝上的概率是 。 15 ． 已 知 反 比 例 函 数 ky x  的 图 像 经 过 点 （ 1 ， － 2 ）， 则 直 线 y = （ k － 1 ） x 的 解 析 式 为 。 三、解答题（本大题共 9 个小题，满分 75 分） 16．（本小题 6 分）解方程： 0672  xx O x y A O x y B O x y C O x D y 17．（本小题 6 分）为响应国家“退耕还林”的号召，改变我省水土流失严重的状况，2005 年我省退耕还 林 1600 亩，计划 2007 年退耕还林 1936 亩，问这两年平均每年退耕还林的增长率是多少？ 18．（本小题 6 分）如图，小明为测量某铁塔 AB 的高度，他在离塔底 B 的 10 米 C 处测得塔顶的仰角α=43°， 已知小明的测角仪高 CD=1.5 米，求铁塔 AB 的高。（精确到 0.1 米） （参考数据：sin43° =0.6820， cos43° =0.7314， tan43° =0.9325） 19．（本小题 8 分）你吃过拉面吗？实际上在做拉面的过程中就渗透着数学知识：一定体积的面团做成拉 面，面条的总长度 y(m)是面条的粗细（横截面积） s (mm2)的反比例函数，其图像如图所示。 （1）写出 y 与 s 的函数关系式； （2）求当面条粗 1.6mm2时，面条的总长度是多少米？ 20．（本小题 8 分）两个布袋中分别装有除颜色外，其他都相同的 2 个白球，1 个黑球，同时从这两个布袋 中摸出一个球，请用列表法表示出可能出现的情况，并求出摸出的球颜色相同的概率。 21．（本小题 8 分）已知：四边形 ABCD 的对角线 AC、BD 相交于点 O，给出下列 5 个条件： ①AB∥DC；②OA=OC；③AB=DC；④∠BAD=∠DCB；⑤AD∥BC。 （1）从以上 5 个条件中任意选取 2 个条件，能推出四边形 ABCD 是平行四边形的有（用序号表示）： 如①与⑤ 、 。（直接在横线上再写出两种） （2）对由以上 5 个条件中任意选取 2 个条件，不能推出四边形 ABCD 是平行四边形的，请选取一种情 形举出反例说明。 22．（本小题 9 分）在如图所示的三角形纸片 ABC 中，∠C=90°，∠B=30°，按如下步骤可以把这个直角 C A B ED α A B D O C 1 20 s(mm2) y(m) O 2 3 4 5 P（4，32） 60 40 80 100 A E 三角形纸片分成三个全等的小直角三角形（图中虚线表示折痕）。①先将点 B 对折到点 A，②将对折后 的纸片再沿 AD 对折。 （1）由步骤①可以得到哪些等量关系？ （2）请证明△ACD≌△AED （3）按照这种方法能否将任意一个直角三角形分成三个全等的小三角形？ 23．（本小题 12 分）如图，已知直线 y =－x＋4 与反比例函数 y k x  的图象相交于点 A（-2，a），并且与 x 轴相交于点 B。 （1）求 a 的值； （2）求反比例函数的表达式； （3）求△AOB 的面积。 九年级数学（参考答案） 一、选择题 1．D 2．A 3．C 4．B 5．C 6．A 7．B 8．D 二、填空题 9．2 10．x1=0, x2=3 11． 2y x  12．30 13．对角线相等的梯形是等腰梯形 14． 1 4 15．y =－3x 三、解答题 16． 解方程得 x1=1，x2=6 17．解： 设平均增长率为 x ，则 1600(1+x)2=1936 解得：x1=0.1=10% x2=－2.1(舍去) 18．解：如图，可知四边形 DCBE 是矩形， 则EB = DC =1.5米，DE=CB=10米 在 Rt△AED中，∠ADE=α=43º C A B ED α x y A O B 那么tanα AE DE  所以，AE=DEtan43º =10×0.9325=9.325 所以，AB=AE+EB =9.325+1.5=10.825≈10.8（米） 19．（本小题 8分） 解：（1）设 y 与 s 的函数关系式为 s ky  ， 将 s=4,y=32代入上式，解得 k=4×32=128 所以 y 与 s 的函数关系式 s y 128  （2）当 s=1.6时， 80 6.1 128 y 所以当面条粗 1.6mm2时，面条的总长度是 80 米 20．（本小题 8分）列表得： 白球的概率= 4 9 黑球的概率= 1 9 21．（本小题 8分） 解：（1）①与②；①与③；①与④；②与⑤；④与⑤ （只要写出两组即可；每写一个给 2 分） （2）③与⑤ 反例：等腰梯形 22．（本小题 9分） 解：（1）AE=BE，AD=BD，∠B=∠DAE=30º， ∠BDE=∠ADE=60º，∠AED=∠BED=90º。 （2）在 Rt△ABC 中，∠B=30º，所以 AE=EB，因而 AC=AE 又因为∠CAD=∠EAD，AD=AD 所以△ACD≌△AED （3）不能 23．（本小题 12分） 解：（1）将 A（－2，a）代入 y=－x＋4 中，得：a=－(－2)+4 所以 a =6 （2）由（1）得：A（－2，6） 将 A（－2，6）代入 x ky  中，得到 2 6   k 即 k=－12 所以反比例函数的表达式为： x y 12  （3）如图：过 A 点作 AD⊥x轴于 D； 因为 A（－2，6） 所以 AD=6 在直线 y=－x＋4 中，令 y=0，得 x=4 所以 B（4，0） 即 OB=4 所以△AOB 的面积 S= 2 1 OB×AD= 2 1 ×4×6=12 24．（本小题 12分） ， ， ，， ， ， ， ， ， （ ） （ ） （ ） （ ） （ ） （ ） （ ） （ ） 黑 黑 黑 （ ） 黑黑黑黑 黑 白 白白 白 白 白白白 白 白 白白 白 白 白白 袋2 袋1 x y A OD B A D B C 解：（1）菱形的一条对角线所在的直线。（或菱形的一组对边的中点所在的直线或菱形对角线 交点的任意一条直线）。 （2）三角形一边中线所在的直线。 （3）方法一：取上、下底的中点，过两点作直线得梯形的二分线（如图 1） 方法二：过 A、D作 AE⊥BC，DF⊥BC，垂足 E、F，连接 AF、DE 相交于 O，过点 O 任意 作直线即为梯形的二分线（如图 2） （如图 1） （如图 2） 九年级数学 一、选择题（每小题 3分，满分 24 分） 1.一元二次方程 2 5 6 0x x   的根是（ ） A．x1=1，x2=6 B．x1=2，x2=3 C．x1=1，x2=-6 D．x1=-1，x2=6 2.下列四个几何体中，主视图、左视图与俯视图是全等图形的几何体是（ ） A．球 B．圆柱 C．三棱柱 D．圆锥 A D B C E F O 3.到三角形三条边的距离相等的点是三角形（ ） A．三条角平分线的交点 B．三条高的交点 C．三边的垂直平分线的交点 D．三条中线的交点 4.如果矩形的面积为 6cm2，那么它的长 y cm 与宽 x cm 之间的函数关系用图象表示 大致（ ） A B C D 5.下列函数中，属于反比例函数的是（ ） A． 3 xy  B． 1 3 y x  C． 5 2y x  D． 2 1y x  6.在 Rt△ABC 中，∠C=90°，a=4，b=3，则 cosA 的值是（ ） A． 4 5 B． 3 5 C． 4 3 D． 5 4 7.如图（1），△ABC 中，∠A=30°，∠C=90°AB 的垂直平分线 （1） 交 AC 于 D 点，交 AB 于 E 点，则下列结论错误的是（ ） A、AD=DB B、DE=DC C、BC=AE D、AD=BC 8.顺次连结等腰梯形各边中点得到的四边形是 （ ） A、矩形 B、菱形 C、正方形 D、平行四边形 二、填空题（每小题 3分，满分 21 分） 9．计算 tan45°= ． 10．已知函数 2 2( 1) my m x   是反比例函数，则 m的值为 ． 11．请你写出一个反比例函数的解析式,使它的图象在第二、四象限 ． 12．在直角三角形中，若两条直角边长分别为 6cm 和 8cm，则斜边上的中线长 为 cm． 13. 已知菱形的周长为 cm40 ，一条对角线长为 cm16 ，则这个菱形的面积 为 (cm) 2. 14．已知正比例函数 kxy  与反比例函数  0 k x ky 的一个交点是（2，3），则另 一个交点是（ ， ）. 15．如图，已知 AC=DB，要使△ABC≌△DCB，需添加的一个 条件是 ． 三、解答题（本大题共 9个小题，满分 75 分） 16．（本小题 8分）解方程： 2 ( 2)x x x   A B C D y xO o y x y xo y xo 17．（本小题 8分）如图，在△ABD 中，C是 BD 上的一点， 且 AC⊥BD，AC=BC=CD．（1）求证：△ABD 是等腰三角形． （2）求∠BAD 的度数． 18．（本小题 8 分）如图所示，课外活动中，小明在离旗杆 AB 的10米 C处，用测角仪测得旗 杆顶部 A 的仰角为 40，已知测角仪器的高 CD=1.5米，求旗杆 AB 的高．（精确到0.1米） （供选用的数据： sin 40 0.64 ， cos 40 0.77 ， tan 40 0.84 ） 19.（本小题 8分）某商店四月份的营业额为 40 万元，五月份的营业额比四月份有所增长， 六月份比五月份又增加了 5个百分点，即增加了 5%，营业额达到了 50.6 万元。求五月份增 长的百分率。 20．（本小题 8 分）“一方有难，八方支援”．今年 11 月 2 日，鄂嘉出现洪涝灾害，牵动着全 县人民的心，医院准备从甲、乙、丙三位医生和 A、B 两名护士中选取一位医生和一名 护士支援鄂嘉防汛救灾工作． （1）若随机选一位医生和一名护士，用树状图（或列表法）表示所有可能出现的结果． （2）求恰好选中医生甲和护士 A的概率． 21．（本小题 8 分）如图，在△ABC 中，AC=BC，∠C=90°，AD 是△ABC 的角平分线，DE⊥AB， 垂足为 E． （1）已知 CD=4cm，求 AC 的长． （2）求证：AB=AC+CD． 40 ED C B A A C E D B 22．（8 分）在如图的 12×24 的方格形纸中（每个小方 格的边长都是 1 个单位）有一ΔABC. 现先把ΔABC 分别 向右、向上平移 8 个单位和 3 个单位得到ΔA1B1C1；再 以点 O 为旋转中心把ΔA1B1C1按顺时针方向旋转 90º得 到ΔA2B2C2. 请在所给的方格形纸中作出ΔA1B1C1和Δ A2B2C2. 23．（本题满分 9分） 如图，给出四个等式：①AE=AD；②AB=AC；③OB=OC；④∠B=∠C. 现选取其中的三个，以两 个作为已知条件，另一个作为结论. （1）请你写出一个正确的命题，并加以证明； （2）请你至少写出三个这样的正确命题. 24、（10 分）如图,已知反比例函数 x ky 2  和一次函数 y=2x-1，其中一次函数的图象经过（a,b）， （a+1，b+k）两点. (1)求反比例函数的解析式； （2）如图4，已知点A在第一象限，且同时在上述两个函数的图象上，求点A的坐标； （3）利用（2）的结果，请问：在 x轴上是否存在点 P，使△AOP 为等腰三角形？若存在， 把符合条件的 P点坐标都求出来；若不存在，请说明理由. 九年级数学参考答案 一、选择题 1．D 2．A 3．A 4．C 5．B 6．B 7．B 8．B 二、填空题 9．1 10．1 11． 1y x   …… 12．5 13．96 (cm)2 14．（-2，-3）15．AB=DC 或 ACB= DBC 三、解答题 16．（8 分） 解方程得 x1=1，x2=2 17．（8 分）解：（1）∵ AC⊥BD，AC=BC=CD ∴ C2 B2 A B C D E O ① ②  ACB= ACD=90°∴ △ACB≌△ACD ∴ AB=AD ∴ △ABD 是等腰三角形．（2）∵ AC⊥BD，AC=BC=CD ∴ △ACB、△ACD 都是等腰直角三角形．∴  B= D=45° ∴  BAD=90° 18．解：在Rt△ADE中， tan ADE= DE AE ∵ DE=10， ADE=40° ∴ AE=DE tan ADE =10 tan 40°≈ 10 0.84 =8.4 ∴ AB=AE+EB=AE+DC=8.4 1.5 9.9  答：旗杆AB的高为9.9米 19.解：设五月份增长率为 x 40（1+x）(1+x+5%)=50.6 解得 x1=0.1,x2=-2.15(舍去) 20．（ 8分）解：（1）用列表法或树状图表示所有可能结果如下： 列 表 法 ： 树状图： （2）P（恰好选中医生甲和护士 A）= 1 6 ， ∴恰好选中医生甲和护士 A 的概率是 1 6 21．（8 分） 解：（1）∵AD 是△ABC 的角平分线，DC⊥AC，DE⊥AB ∴DE=CD=4cm， 又∵AC=BC，∴∠B=∠BAC， 又∵∠C=90º，∴∠B=∠B DE=45º，∴BE=DE 在等腰直角三角形 BDE 中，由勾股定理得，BD=4 2 cm ∴AC=BC=CD+BD=4+4 2 (cm) （2）由（1）的求解过程可知：△ACD≌△AED，∴AC=AE， 又∵BE=DE=CD ∴AB=AE+BE=AC+CD 22.解：（8 分）.ΔA1B1C1和ΔA2B2C2如图所示. 23．（9 分）（1）如果 AE=AD，AB=AC，那么∠B=∠C. 证明：在ΔABE 和ΔACD 中，∵AE=AD，∠A=∠A，AB=AC，∴ΔABE≌ΔACD，∴∠B=∠C. （2）①如果 AE=AD，AB=AC，那么 OB=OC. ②如果 AE=AD，∠B=∠C，那么 AB=AC. ③如果 OB=OC， ∠B=∠C，那么 AE=AD. 24.（10 分）解：（1）由题意得      1)1(2 12 akb ab ②－①得 2k ∴反比例函数的解析式为 x y 1  . (2)由       x y xy 1 12 解得      1 1 1 1 y x ，       2 2 1 2 2 y x ∵点 A在第一象限，∴点 A 的坐标为（1，1） （3） 211 22 OA ，OA 与 x轴所夹锐角为 45°， ①当 OA 为腰时，由 OA=OP 得 P1（ 2 ，0），P2（－ 2 ，0）；由 OA=AP 得 P3=（2，0）. ②当 OA 为底时，得 P4=（1，0）. ∴符合条件的点有 4 个，分别是（ 2 ，0），（－ 2 ，0），（2，0），（1，0） enjoy the trust of得到...的信任 have / put trust in信任 in trust受托的，代为保管的 take .一．选择题（本题有 10小题，每小题 2 分，共 20分） A B 甲 （甲， A） （甲， B） 乙 （乙， A） （乙， B） 丙 （丙， A） （丙， B） 护 士医 生 C 1．方程中，是关于 x的一元二次方程的是 （ ）A.    1213 2  xx B. 0211 2  xx C. 02  cbxax D. 12 22  xxx 2．若反比例函数的图象经过（2，-2），（m，1）,则 m= （ ） A．1 B．-1 C．4 D．-4 3．有一透明实物如图，那么它的主视图是 （ ） A B C D 4．如图，在等腰梯形 ABCD 中，AB∥CD，DC = 3 cm，∠A=60°，BD 平分∠ABC，则这个梯形的周长是（ ） A. 21 cm B. 18 cm C. 15 cm D. 12 cm 5．三角形两边长分别为 3和 6，第三边是方程 2 6 8 0x x   的解，则这个三角形的周长是（ ）A．11 B.13 C.11 或 13 D.11 和 13 6．小明用两根同样长的竹棒做对角线，制作四边形的风筝，则该风筝的形状一定是（ ）A 矩形 B 正方形 C 等腰梯形 D 无法确定 7．既是轴对称，又是中心对称图形的是 （ ） A．矩形 B．平行四边形 C．正三角形 D．等腰梯形 8．中央电视台“幸运 52”栏目中的“百宝箱”互动环节，是一种竞猜游戏，游戏规则如下：在 20 个商标牌中，有 5 个商标牌的 背面注明一定的奖金额，其余商标的背面是一张哭脸，若翻到哭脸就不得奖金，参与这个游戏的观众有三次翻牌的机会(翻 过的牌不能再翻) ．某观众前两次翻牌均获得若干奖金，那么他第三次翻牌获奖的概率是 （ ）A. 4 1 B. 5 1 C. 6 1 D. 20 3 9.一元二次方程 2 5 6 0x x   的根是（ ） A．x1=1，x2=6 B．x1=2，x2=3 C．x1=1，x2=-6 D．x1=-1，x2=6 10.下列四个几何体中，主视图、左视图与俯视图是全等图形的几何体是（ ） A．球 B．圆柱 C．三棱柱 D．圆锥 11.到三角形三条边的距离相等的点是三角形（ ）A．三条角平分线的交点 B．三条高的交点 C．三边的垂直平分线的 交点 D．三条中线的交点 12.如果矩形的面积为 6cm 2 ，那么它的长 y cm 与宽 x cm 之间的函数关系用图象表示 大致（ ） A B C D A B CD A B C y xO o y x y xo y xo y xo 13.下列函数中，属于反比例函数的是（ ） A． 3 xy  B． 1 3 y x  C． 5 2y x  D． 2 1y x  14.如图（1），△ABC 中，∠A=30°，∠C=90°AB 的垂直平分线交 AC于 D点，交 AB 于 E点，则下列结论错误的是（ ） A、AD=DB B、DE=DC C、BC=AE D、AD=BC 15.顺次连结等腰梯形各边中点得到的四边形是 （ ） A、矩形 B、菱形 C、正方形 D、平行四边形 16.已知 3是关于 x的方程 3 4 x2-2a+1=0 的一个解，则 2a 的值是【 】 （A）11 （B）12 （C）13 （D）14 17.已知直角三角形的两边长是方程 x 2 -7x+12=0 的两根，则第三边长为【 】 （A）7 （B）5 （C） 7 （D）5 或 7 18.下列命题中错误的【 】 （A）两对邻角互补的四边形是平行四边形；（B）一组对边平行，一组对角相等的四边形是平行四边形 C等腰梯形的对角线 相等（D）平行四边形的对角线互相平分。 19.如图，在直角坐标系中，直线 y=6-x 与函数 y= x 4 (x＞0)的图象 相交于点 A、B，设点 A的坐标为(x1，，y1)，那么长为 x1,宽为 y1 的矩形的面积和周长分别为【 】 （A）4，12 （B）8，12 （C）4，6 （D）8,6 20．如图右，在双曲线上取一点 A向 x轴引 垂线，垂足为 B，连结 OA，若△AOB 的面积为 3 则双曲线的函数关系式为（ ） A、 x y 3  B、 x y 3  C、 x y 6  D、 x y 6  21．一元二次方程 23 0x x  的解是（ ） A． 0x  B． 1 20 3x x ， C． 1 2 10, 3 x x  D． 1 3 x  22．下列各点，在反比例函数 x y 6  的图像上的是（ ） A、（-2，-3） B、（1,6） C、（-3,2） D、（-6，-1） 23．某农场的粮食总产量为 1500 吨，设该农场人数为 x人，平均每人占有粮食数为 y 吨，则 y 与 x之间的函数图象大致 是（ ） o A B x y 0 x y 0 y 0 A． B． 24. 已知关于 x的一元二次方程   0131 22  kxxk 有一根为 0，则 k=( ) A、1 B、-1 C、 1 D、 0 25. 2010 年某市政府投资 2亿元人民币建设了廉租房 8万平方米，预计到 2012 年底三年共累计投资 9.5 亿元人民币建设廉 租房，若在这两年内每年投资的增长率相同．设每年市政府投资的增长率为 x，根据题意，列出方程为（ ） A 22 1+ ) 9 .5x （ B． 22 1+ ) 2(1 ) 9.5x x  （ C 22+2 1 ) 2(1 ) 9.5x x   （ D． 28 8 1+ ) 8(1 ) 9.5x x   （ 26．若关于 x的方程 0962  xkx 有实数根，则 k 的取值范围是（ ） A． 1k  B． 1k  C． 1 0k k 且 D． 1 0k k 且 27.已知方程 的一个根为 ，则另一个根是（ ） A.5 B. C. D.3 28.如图，四边形 ABCD是矩形，F是 AD上一点，E是 CB延长线上一点，且四边形 AECF是等腰梯形，下列结论中，不一定 正确的是（ ） A.AE=FC B.AD=BC C.BE=AF D.∠E=∠CFD 29.如图，在菱形 中，对角线 、 相交于点 O，E为 BC的中点，则下列式子中，一定成立的是（ ） A. B. C. D. 30.在反比例函数 的图象的每一条曲线上， 都随 的增大而增大，则 的值可以是（ ）A.2 B.1 C.0 D. －1 31.用电器的输出功率 与通过的电流 、用电器的电阻 之间的关系是 ，下面说法中，正确的是（ ） A. 为定值， 与 成反比例 B. 为定值， 与 成反比例 C. 为定值， 与 成正比例 D. 为定值， 与 成正比例 32．如图所示的两个转盘中，指针落在每一个数上的机会均等， 那么两个指针同时落在偶数上的概率是（ ） A. 19 25 B. 10 25 C. 6 25 D. 5 25 33．下列命题中，不正确．．．的是（ ） A．对角线相等的平行四边形是矩形． B．有一个角为 60°的等腰三角形是等边三角形．C．正方形的两条对角线相等且互相 A B C D E F 第 28 题图 D A B C EO 第 29 题图 垂直平分． D．直角三角形斜边上的高等于斜边的一半 34．某公司把 500 万元资金投入新产品的生产，第一年获得一定的利润，在不抽掉资金和利润的前提下，继续生产，第二 年的利润率比第一年提高 8%，若第二年的利润达到 112万元，设第一年的利润率为 x，则方程可以列为（ ） A．500(1+x)(1+x+8%)=112 B．500(1+x)(1+x+8%)=112 +500 C．500(1+x)·8%=112 D．500(1+x)(x+8%)=112 35. 已知点（－2，y1），（－1，y2），（3，y3）都在反比例函数 x 6y  的图象上，那么 y1、y2 、y3的大小关系正确的是（ ） A．y2BM. (1)写出 AB，AM，BM 之间的比例式；(2)如果 AB＝12 cm，求 AM 与 BM 的长． 6.如图所示，以长为 2 的定线段 AB 为边作正方形 ABCD，取 AB 的中点 P，连接 PD，在 BA 的延长线上取点 F，使 PF＝PD，以 AF 为边作正方形 AMEF，点 M 在 AD 上． (1)求 AM，DM 的长； (2)点 M 是 AD 的黄金分割点吗？为什么？ 二、能力提升 7．五角星是我们常见的图形，如图是一个标准的正五角星，其中，点 C，D分别是线段 AB 的黄金分割点， AB＝20cm，求 EC＋CD 的长． 第四章 图形的相似 第 6 节 利用相似三角形测高 学习目标：（1）掌握几种测量旗杆高度的方法与原理 （2）解决一些较简单的相关生活实际问题 学习重难点：（1）通过设计测量旗杆高度的方案，学会将实物图形抽象成几何图形的方法 （2）体会将实际问题转化成数学模型的转化思想 预习案 一、预习教材 P 103—P104 二、感知填空 1、相似三角形的定义：三角 相等，三边 的两个三角形叫做相似三角形。 2、三角形相似的判定： 三、自主提问 探究案 探究问题：学校操场上的国旗旗杆的高度是多少？你有什么办法测量？ 探究一：利用阳光下的影子测量旗杆的高度： 让一名同学恰好站在旗杆影子的顶端，然后一部分同学测量该同学的影长，另一部分同学测量同一时 刻旗杆的影长。 原理：∵太阳是平行光线 ∴AB∥CD，∠B=∠DCE ∵∠ACB=∠DEC=90° ∴△ACB∽△DEC ∴ BC CEACDE CE BC DE AC   即, 结论：同一时刻， 参照物体影子的长度 参照物体高度 被测物体影子长度 被测物体实际高度  探究二：利用标杆测量旗杆的高度 工具：皮尺、标杆 步骤：（1）测量出标杆 CD 的长度，测出观测者眼部以下高度 EF； （2）让标杆竖直立于地面，调整观测者 EF 的位置，当旗杆顶部、标杆顶端、观测者的眼睛三 者在同一条直线上，测出观测者距标杆底端的距离 FD 和距旗杆底部的距离 FB； （3）根据 EH EG AH CG  ,求得 AH 的长，再加上 EF 的长即为旗杆 AB 的高度。 依据：如图，过点 E 作 EH⊥AB 于点 H，交 CD 于点 G ∵CD∥AB ∴∠ECG=∠EAH ∵∠CEG=∠AEH ∴△ECG∽△EAH ∴ EH EG AH CD  ∵EG=FD,EH=FB,CG=CD-GD=CD-EF, 且 FD，FB,CD,EF 可测 ∴可求 AH 的长度 ∴AB=AH+HB=AH+EF 探究三：利用镜子的反射杆测量旗杆的高度 工具：皮尺、镜子 步骤：（1）在观测者与旗杆之间放一面镜子，在镜子上做一个标记； （2）测出观测者眼睛到地面的距离； （3）观测者看着镜子来回移动，直至看到旗杆顶端在镜子中的像与镜子上的标记重合，此时测 出镜子上标记 O 到人脚底 D的距离 OD 及镜子上的标记 O 到旗杆底部的距离 OB； （4）把测得的数据代入 OB OD AB CD  ,即可求得旗杆的高度 AB。 依据：在△COD 与△AOB 中 ∵∠COD=∠AOB，∠CDO=∠ABO=90° ∴△COD∽△AOB ∴ OB OD AB CD  ∵CD,OD,OB 皆可测得 ∴ AB 可求。 跟踪练习：如图所示，从点 A（0,2）发出的一束光，经 x轴反射，过点 B（4,3），则这束光从点 A 到点 B 所经过路径的长为 。 作 业 案 1、在同一时刻同一个地点物体的高度与自身的影长的关系是( ) A.成反比例 B.成正比例 C.相等 D.不成比例 2. 如图，小东用长为 3.2m 的竹竿做测量工具测量学校旗杆的高度，移动竹竿，使竹竿、旗杆顶端的影子 恰好落在地面的同一点．此时，竹竿与这一点相距 8m，与旗杆相距 22m，则旗杆的高为（ ） A、12m B、10m C、8m D、7m 3、如图，测量小玻璃管口径的量具 ABC ， AB 的长为 12cm，AC 被分为 60 等份．如果小玻璃管口 DE 正 好对着量具上 20 等份处（DE∥AB），那么小玻璃管口径 DE 是（ ） A、8cm B、10cm C、20cm D、60cm 第 2 题 第 3 题 4、如图,DE⊥EB,AB⊥EB,∠DCE=∠ACB,DE=12 m,EC=15 m,BC=30 m,则 AB =____m. 5、某一时刻,测得旗杆的影长为 8 m,李明测得小芳的影长为 1 m,已知小芳的身高为 1.5 m,则旗杆的高度是 _______________m. A B 6、如图，铁道口的栏杆短臂长 1m，长臂长 16m．当短臂端点下降 0.5m 时，长臂端点升高______m（杆的 宽度忽略不计）． 第 4 题 第 6 题 7、如图所示,要测量河两岸相对的两点 A,B 的距离,先从 B 处出发与 AB 成 90°角方向,向前走 80 米到 C 处立一标杆,然后方向不变向前走 50 米至 D 处,在 D 处转 90°,沿 DE 方向走 30 米,到 E 处,使 A(目标 物),C(标杆)与 E 在同一条直线上,那么可测得 A,B 间的距离_______. 7 题 第 8 题 8、如图,为了测量一棵树 CD 的高度,测量者在 B 点立一高为 2 米的标杆,观测者 从 E 处可以看到杆顶 A,树顶 C 在同一条直线上.若测得 BD=23.6米,FB=3.2 米,EF=1.6 米,求树高. 9．（能力提升）一位同学想利用树影测出树高，他在某时刻测得直立的标杆高 1米，影长是 0.9 米，但他 去测树影时，发现树影的上半部分落在墙 CD 上，（如图所示）他测得 BC= 2．7 米，CD=1.2 米。试求出树 高为多少米？ 第四章 图形的相似 第 7 节 相似三角形的性质(一) 学习目标：（1）探索 相似三角形对应线段（高、中线、角平分线）的比等于相似比 （2）会利用相似三角形的性质求线段的长 学习重难点：理解并能较熟练应用相似三角形的性质 预习案 一、预习教材 P 106—P107 二、感知填空 1、相似三角形的定义：三角 相等，三边 的两个三角形叫做相似三角形。 2、全等三角形的性质：全等三角形的对应角 、对应边 、对应角的平分线 、对应边 上的中线 、对应边上的高 3、相似三角形的性质：相似三角形的对应角______，对应边________； 相似三角形的对应高之比、对应角平分线之比、对应中线之比都等于______； 三、自主提问 探究案 探究一：相似三角形的对应高之比、对应角平分线之比、对应中线之比都等于相似比 跟踪练习： 1.△ABC∽△A1B1C1，AB=4，A1B1=12，则它们对应边上的高的比是 ，若 BC 边上的中线为 1.5，则 B1C1上的中线 A1D1=_______ 2.如图,在正方形网格上有△A1B1C1和△A2B2C2， 这两个三角形相似吗？如果相似，求出△A1B1C1 和△A2B2C2的相似比． 探究二：如图，AB⊥BC，DC⊥BC，垂足分别为 B、C，且 AB=8，DC=6， BC=14，BC 上是否存在点 P使△ABP 与△DCP 相似？若有，有几个？ 并求出此时 BP 的长，若没有，请说明理由 作业案 1、两个相似三角形一组对应角平分线的长分别是2 cm和5 cm，那么这两个三角形的相似比是 ， 如 果在这两个三角形的一组对应中线中，较短的中线是3 cm，那么较长的中线是 cm. 2、在△ABC 中，BC=54cm，CA=45cm，AB=63cm，若另一个与它相似的三角形的最短边长为 15cm，则其周长 为_____ 3、顺次连接三角形三边上的中点所构成的三角形的高与原三角形对应高的比为 4、在 Rt△ABC 中，CD 是斜边 AB 上的高，若 BD=9，DC=12，则 AD=_____，BC=_____ 5、如图，圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后，在地面上形成阴影．已知桌面的直径 为1．2 m，桌面距离地面1 m．若灯泡距离地面3 m，则地面上阴影部分的面积为 ( ) A．0．36πm 2 B．0．81πm 2 C．2πm 2 D．3.24πm 2 6、如图，在大小为 4×4 的正方形方格中，△ABC 的顶点 A、B、C在单位正方形的顶点上，请在图中画一个△DEF， 使△DEF∽△ABC（相似比不为 1），且点 D、E、F 都在单位 正方形的顶点上 7、正方形 ABCD 中，E、F 分别是边 BC、CD 上的点， 3 1EB CE ， CF=FD，连接 AE、EF、AF，你能找出图中所有的相似三角形吗？ 试说明理由 (第 3 题) B C A D P F C A B D E A B C 8、（能力提升）如图,要在底边 BC=160cm,高 AD=120cm 的△ABC 铁皮余料上 截取一个矩形 EFGH,使点 H在 AB 上,点 G在 AC 上,点 E,F 在 BC 上,AD 交 HG 于点 M,此时有 AM/AD=HG/BC (1)设矩形 EFGH 的长 HG=y,宽 HE=X,确定 y 与 X 的函数关系式 第四章 图形的相似 第 7 节 相似三角形的性质(二) 学习目标：（1）探索相似三角形的周长比与面积比 （2）猜想相似多边形的周长比与面积比，体验类比思想 教学难点、重点：利用相似三角形的性质求相似三角形的周长、面积比 预习案 一、预习教材 P 109—P110 二、感知填空 1、如果两个相似三角形对应边的比为 3∶5 ，那么它们的相似比为________，周长的比为_____，面积的 比为_____． 2、如果两个相似三角形面积的比为 3∶5 ，那么它们的相似比为________，周长的比为________． 三、自主提问 探究案 探究一：相似三角形的周长比等于相似比，面积比等于相似比的平方 A GH CB DE M F 跟踪练习： 1、如果两个相似三角形的周长为 6cm 和 15cm，那么两个相似三角形的相 似比为_______ 2、两个相似三角形对应的中线长分别是 6 cm 和 18 cm，若较大三角形的 周长是 42 cm ，面积是 12 cm 2 ，则较小三角形的周长为________cm，面积为_______cm 2 ． 探究二：如图，△ABC 中，DE∥BC， （1）若 3 2 EC AE  ，① 求 AC AE 的值； ② 求 ABC ADE S S   的值； ③ 若 5S ABC  ，求△ADE 的面积； （2）若 SS ABC  ， 3 2 EC AE  ，过点 E 作 EF∥AB 交 BC 于 F，求□BFED 的面积； （3）若 k EC AE  ， 5ABCS ，过点 E作 EF∥AB 交 BC 于 F，求□BFED 的面积． 跟踪练习： 连结三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______， 面积比等于_______． 作业案 1、已知△ABC∽△DEF，且AB：DE=1：2．则△ABC的面积与△DEF的面积之比为 ____ 2、若△ABC∽△DEF，且△ABC 与△DEF 的相似比为 1：2．则△DEF 与△ABC 的周长比为_____ 源: 3、已知甲、乙两个多边形相似，其相似比为 2:5；若多边形甲的周长为 24，则多边形乙的周长 为 ；若两个多边形的面积之和为 174，则多边形甲的面积为 4、在梯形 ABCD 中，AD∥BC，对角线 BD 分成的两部分面积的比是 1：2， EF 是中位线，则被 EF 分成的两 部分面积的比 S 四边形 AEFD：S 四边形 BCEF=_______ 。 5、△ABC∽△A1B1C1，且△ABC 的周长与△A1B1C1 的周长之比为 11：13，又 A1B1－AB=1cm，则 AB=_____cm， A1B1=_______cm。 6．若两个相似多边形的面积之比为 1：4．周长之差为 6，则这两个相似多边形的周长分别是 7、在△ABC 中，已知 DE∥BC，AE=3EC，S△ABC=48， 求△ADE 及四边形 BCED 的面积。 8、（能力提升）如图，平行四边形 ABCD 中，E 为 DC 边上一点，连接 AE 并延长交 BC 的延长线于 F，在这 个图形中，有哪几对相似三角形？你是怎么判断的？若 2 1BC CF ，AD 的长为 6，求 BF 的长及 DC CE 的 值。 第四章 图形的相似 第 8 节 图形的位似 （一） 学习目标：（1）了解位似图形的概念及性质 （2）知道利用位似的性质可以将一个图形放大或缩小 学习重难点：会画一个简单图形的位似图形 O F A B C D E 预习案 一、预习教材 P 113—P114 二、感知填空 1、相似多边形： 、 的两个多边形叫做相似多边形； 2、相似多边形的性质： 三、自主提问 探究案 探究一：观察下面几幅图形有什么共同特征 归纳：位似多边形的概念 如果两个相似多边形任意一组对应顶点 P，P’所在的直线都经过同一点 O，且有 OP’=k·OP（k ≠0），那么这样的两个多边形叫做位似多边形，点 O 叫做位似中心，k 就是相似比。 探究二：位似多边形的性质 如图 总结：1、位似多边形上任意一对对应点到位似中心的距离之比等于位似比； 2、 位似多边形上对应点和位似中心在同一条直线上； 3、 位似多边形上的对应线段平行或在同一条直线上； 4、 位似多边形是特殊的相似图形，因此位似图形具有相似图形的一切性质。 探究三: 位似多边形的画法 把图 1 中的四边形 ABCD 缩小到原来的 2 1 ． （4）作法一： 作法二： 作法三： 同学们试一试 归纳步骤：（1）确定位似中心； （2）确定原图形的关键点。通常是多边形的顶点； （3）确定相似比； （4）找出新图形的对应关键点； （5）顺次连接各点，得到放大或缩小的图形。 作业案 1．如图，五边形 ABCDE 与五边形 A′B′C′D′E′是位似图形，O 为位似中心，OD＝ 1 2 OD′，则 A′B′:AB 为（ ） A.2:3 B.3:2 C.1:2 D.2:1 2．如图，△DEF 是由△ABC 经过位似变换得到的，点 O 是位似中心，D，E，F 分别是 OA，OB，OC 的中点， 则△DEF 与△ABC 的面积比是（ ） A．1︰2 B．1︰4 C．1︰5 D．1︰6 3.如图，其中属于位似图形的有____________(填序号)． 4.如图，A′B′∥AB，B′C′∥BC，且 OA′∶A′A=4∶3，则△ABC 与△ 是位似图形，位似比为 ；△OAB 与△ 是位似图 形，位似比为 . A B C E D OB A C D E 5．已知五边形 ABCDE 和点 O，请你以 O 为位似中心画五边形 ABCDE 的位的图形 A′B′C′D′E′，使得相 似比＝ 2 1 ，即 2 1  BA AB 6．如图，△ABC 三个顶点的坐标分别为 A (2，7)，B (6，8)，C (8，2)，请你分别完成下面的作图并标 出所有顶点的坐标。(不要求写出作法) （1）以 O为位似中心，在第三象限内作出△A1B1C1，使△A1B1C1与△ABC 的位似比为 1∶2； （2）以 O 为旋转中心，将△ABC 沿顺时针方向旋转 90°得到△A2B2C2。 第 5 题 第 6 题 7. （能力提升）画一个任意三角形，以三角形其中一个顶点为位似中心作一个与原三角形位似的新三角 形，使新三角形与原三角形的位似比为2:1. 第四章 图形的相似 第 8 节 图形的位似 （二） 学习目标：（1）会在坐标系中作位似图形 （2）会利用位似变换求点的坐标 学习重难点：利用位似变换求点的坐标 预习案 y B C A O x 一、预习教材 P 115—P116 二、感知填空 关于对位似图形的表述，下列命题正确的是 。（只填序号） 1、相似图形一定是位似图形，位似图形一定是相似图形； 2、位似图形一定有位似中心； 3、如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个点， 那么，这两个图形是位似图形； 4、位似图形上任意两点与位似中心的距离之比等于位似比。 三、自主提问 探究案 探究一：平面直角坐标系中的位似变换 如图，△AOB 以 O 位似中心，扩大到△COD， 各点坐标分别为：A（1，2）、B（3，0）、D（4，0） 求点的 C坐标 跟踪练习： 如图，以某点为位似中心，将△AOB 进行 位似变换得到△CDE，记△AOB 与△CDE 对应边的比为 k，则位似中 心的坐标和 k 的值分别为（ ） A. (0 0)， ，2 B. (2 2)， ， 1 2 C. (2 2)， ，2 D. (2 2)， ，3 探究二: 位似多边形对应点的坐标变化规律 如图，△ABC 中，A，B两个顶点在 x 轴的上方，点 C 的坐标是(－1，0),以点 C 为位似中心，在 x 轴的下方作△ABC 的位似图形，并把△ABC 的边长放大到原来的 2 倍，记所得的像是△A′B′C。设点 B 的对应点 B′的横坐标是 a，则点 B的横坐标是多少？ 归纳： 在平面直角坐标系中，将一个多边形每个顶点的横纵 坐标都乘以同一个数 k（k≠0），所对应的图形与原图形位似，位 似中心是坐标原点，它们的相似比是 k 。 跟踪练习：已知△ABC 与△DEF 是以原点为位似中心的位似图形，位似比为 3 2 ，则 A（－1，1）的对应点 D 的坐标为 作业案 1.如图，三个矩形中相似的是 ( ) A．甲和乙 B．乙和丙 C．甲和丙 D．没有相似矩形 2. 已知：E（－4，2），F（－1，－1），以 O 为位似中心，按比例尺 1∶2，把△EOF 缩小，则点 E 的对应 点 E′的坐标为（ ） A．（2，－1）或（－2，1） B．（8，－4）或（－8，4） C．（2，－1） D．（8，－4） 3. △ABC 三个顶点的坐标分别为 A（2，2），B（4，2），C（6，4），以原点 O 为位似中心，将△ABC 缩小， 使变换后得到的△DEF 与△ABC 对应边的比为 1∶2，则线段 AC 的中点 P 变换后对应的点的坐标 为： 。 4. 如图，已知△OAB 与△OA′B′是相似比为 1∶2 的位似图形，点 O为位似中心，若△OAB 内一点 P（x， y）与△OA′B′内一点 P′是一对对应点，则 P′的坐 标是 5． 如图，已知图中的每个小方格都是边长为 1的小正 方形，每个小正方形的顶点称为格点。若 ABC△ 与 A B C  △ 是位似图形，且顶点都在格点上，则位似中 心的坐标是 。 6.如图，在边长为 1 个单位长度的小正方形组成的网格中，按要求画出△A1B1C1和△A2B2C2； （1）把△ABC 先向右平移 4个单位，再向上平移 1个单位，得到△A1B1C1； （2）以图中的O为位似中心，将△A1B1C1作位似变换且放大到原来的两倍，得到△A2B2C2． 7. （能力提升）如图，在平面直角坐标系中， ABC 的顶点坐标为 )3,2(A 、 )2,3(B 、 )1,1(C 。 （1）若将 ABC 向右平移 3 个单位长度，再向上平移 1 个单位长度，请画出平移后的 111 CBA ； （2）画出 111 CBA 绕原点旋转 180 后得到的 222 CBA ； （3） ''' CBA 与 ABC 是位似图形，请写出位似中心的坐标： ； （4）顺次连结C、 1C 、 'C 、 2C ，所得到的图形是轴对称图形吗？ B' A' C' 3 CB A -4 -3 -2 -1 y 4 2 1 x432-1-2-3-4 O 1 第 6 题 第 7 题