九年级数学上册第二十四章圆24-1圆垂径定理圆心角圆周角124-1 25页

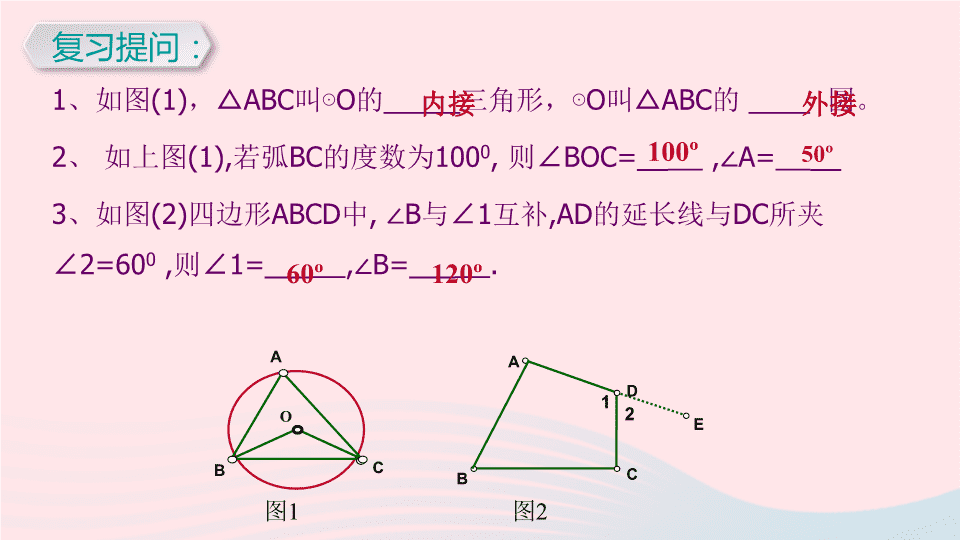
第 24 章 24.1圆、、垂径定理、圆心角、圆周角（1） 24.1.4圆内接四边形 学习目标 ： 1. 理解圆内接四边形和多边形的外接圆的概念，掌握圆内接四边形的性质，并会用此性质进行有关的计算和证明。 2. 进一步掌握圆周角定理及推论，并会综合运用知识进行有关的计算和证明。 3. 学习中注重培养自己的逻辑思维能力、分析、解决问题能力。 1 、如图 (1) ，△ ABC 叫⊙ O 的 _____ 三角形，⊙ O 叫△ ABC 的 ____ 圆。 2 、 如上图 (1), 若弧 BC 的度数为 100 0 , 则∠ BOC=__ ,∠A= __ 3 、如图 (2) 四边形 ABCD 中 , ∠B 与∠ 1 互补 ,AD 的延长线与 DC 所夹∠ 2=60 0 , 则∠ 1=___ ,∠B=___ . 复习提问： A B C E D C B A 2 1 图 1 图 2 O 内接 外接 100 º 50 º 120 º 60 º O C A B D 如图，四边形 ABCD 为圆内接四边形；⊙ O 为四边形 ABCD 外接圆 . 问题 1 若一个多边形各顶点都在同一个圆上，那么，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆。 O B C D E F A O A C D E B 返回 问题 2 C O D B A 如图：圆内接四边形 ABCD 中， ∵ ∠ A 的度数等于弧 BCD 的一半，∠ BCD 的度数等于弧 BAD 的一半， 又∵弧 BCD+ 弧 BAD 度数为 360° ， ∴∠ A ＋∠ C ＝ 180°. 同理∠ B ＋∠ D ＝ 180°. 圆内接四边形的对角互补。 问题 3 如果延长 BC 到 E ，那么 ∠ DCE ＋∠ BCD ＝ 180°. ∴∠ A ＝∠ DCE . 又 ∵∠ A ＋∠ BCD ＝ 180° ， C O D B A E 如果延长 BC 到 E ，那么∠ A 与∠ DCE 会有怎样的关系呢？ A E C O D B 又 ∠ A ＋∠ BCD=180° ∴∠ A ＝∠ DCE ∵∠ DCE ＋∠ BCD ＝ 180° 因为∠ A 是与∠ DCE 相邻的内角∠ DCB 的对角，我们把 ∠ A 叫做∠ DCE 的内对角。 圆内接四边形的一个 外角 等于它的 内对角 。 C O D B A E ∠ A ＝∠ DCE 　　　几何表达式： 　　　∵　四边形 ABCD 内接于⊙ O ， 　　　∴ ∠ A+∠C=180° 且∠ B=∠1 . 性质定理： 探索结论 先根据图形讨论，然后用语言归纳为 : 圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角。 1 2 O O F A B E C D 应用举例 例 如图⊙ O1 与⊙ O2 都经过 A 、 B 两点，经过点 A 的直线 CD 与⊙ O1 交于点 C ，与⊙ O2 交于点 D 。经过点 B 的直线 EF 与⊙ O1 交于点 E ，与⊙ O2 交于点 F 。 求证： CE∥DF CE∥DF 　 ∠ E ＋∠ F ＝ 180° ∠ E ＋∠ 1 ＝ 180° 、∠ 1 ＝∠ F ABEC 是⊙ O 1 的内接四边形 ABFD 是⊙ O 2 的内接四边形 连结 AB 1 2 O O F A B E C D 1 思路分析 反思与拓展 证明两条直线 平行 的方法很多，但常用的还是通过证明 同位角相等、内错角相等、同旁内角互补 等方法。刚才我们通过同旁内角互补证明了 CE ∥ DF ，想一想还能否通过同位角相等或者内错角相等证明结果？ 方法二 延长 EF, 是否有 ∠ E=∠BAD ＝ ∠ 1 ？ 延长 DF, 　能否证明 ∠ E ＝∠２＝∠ 3 ？ 方法三 变式 1 ： 如图，⊙ O 1 和⊙ O 2 都经过 A 、 B 两点，过 A 点的直线 CD 与⊙ O 1 交于点 C ，与⊙ O 2 交于点 D ，过 B 点的直线 EF 与⊙ O 1 交于点 E ，与⊙ O 2 交于点 F 。 E D C F A B 猜想： CE∥DF 仍然成立吗？ O 1 O 2 变式 2: 如图 ,⊙O 1 和⊙ O 2 有两个公共点 A﹑B ，过 A﹑B 两点的直线分别交⊙ O 1 于 C 、 E, 交⊙ O 2 于 D 、 F ，且 CD∥EF 。 C E A B D F O 1 O 2 求证： CE=DF 180 ° 180 ° 100 ° 80 °   50 ° 130 ° 　 45 ° 达标练习 一、填空 (1) 四边形 ABCD 内接于⊙ O ，则∠ A+∠C=__ ， ∠ B+∠ADC=_____; 若∠ B=800 ， 则∠ ADC=______ ∠CDE=______( 图 1)(2) 四边形 ABCD 内接于⊙ O ，∠ AOC=1000 则∠ B=______∠D=______( 图 2) (3) 四边形 ABCD 内接于⊙ O, ∠A:∠C=1:3, 则∠ A=_____, 达标练习 图 2 图 1 (4) 如图 3 ，梯形 ABCD 内接于⊙ O,AD∥BC, ∠B=75 0 , 则∠ C=_____. 2 、选择题： 圆内接平行四边形必为 ( ) A. 菱形 B. 矩形 C. 正方形 D. 等腰梯形 75 ° B 返回 图 3 3 、 如图，四边形 ABCD 为⊙ O 的内接四边形，已知∠ BOD=100° ，则∠ BAD= ∠BCD= 反馈练习： A B C D O 50 º 130 º 4 、圆内接四边形 ABCD 中 ,∠A:∠B:∠C= 2:3:4, 则∠ A= ∠B= ∠C= ∠D= 60 º 90 º 120 º 90 º 5 、如图，四边形 ABCD 内接于⊙ O ， ∠ DCE=75 º ， 则∠ BOD= 150 º A B C D O E 本节课所学的内容可概括为三个“ 1 ”. 一个概念： 圆的内接四边形； 一个定理： 圆的内接四边形的性质定理； 添辅助线的方法： 作两圆的公共弦 . 课堂小结 1 、 圆内接四边形 ------ 顶点在圆上的四边形 , 该圆叫四边形的外接圆。 2 、 圆内接四边形的性质 3 、解题时应注意两点： （ 1 ）注意观察图形，分清四边形的外角和它的内对角的位置，不要受背景的干扰。 （ 2 ）证题时，常需添辅助线 ----- 两圆共有一条弦 ( 公共弦 ) ，构造圆内接四边形。 思维拓展 : 1 、圆内接 平行四边形 一定是 形。 2 、圆内接 梯形 一定是 形。 3 、圆内接 菱形 一定是 形。 矩 等腰梯 正方