全国中学生物理竞赛课件14：刚体动力学运动学问题 42页

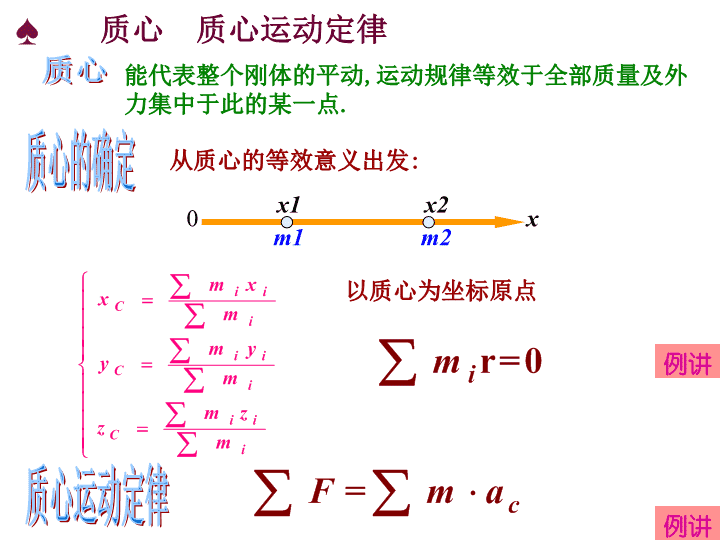
刚体♠ 不发生形变的理想物体 实际物体在外力作用下发生的形变效应不显著可被忽略 时,即可将其视作刚体． 刚体内各质点之间的距离保持不变 刚体的平动与转动♠ 刚体运动时，其上各质点的运动状态（速度、加速度、 位移）总是相同，这种运动称为平动． 刚体运动时，如果刚体的各个质点在运动中都绕同一 直线做圆周运动，这种运动称为转动，而所绕直线便 称为轴．若转轴是固定不动的，刚体的运动就是定轴 转动． 刚体内各质点角速度总相同 质心 质心运动定律♠ 能代表整个刚体的平动,运动规律等效于全部质量及外 力集中于此的某一点. 从质心的等效意义出发: 0 xx1 x2 m1 m2 i i C i i i C i i i C i m xx m m yy m m zz m                以质心为坐标原点 r=0im = cF m a  例讲 例讲 x i tan-1k H  = Hh nn    2 =i H Hm ki n n        O 1 lim n i in i c m x x V      2 1 2 lim / 3 n n i H H Hki in n n kH             3 4 1 13 lim n n i H i n    3 4Cx H x y 0 = 2 nn    R i = 2i i n  i  2 1 2lim 2 cos ( cos ) sin = n i i in i C m R R R Rx m            2 1 4lim cos sin n i in i R           1 lim sin3 sin n i in i R          1 lim sin3 sin n i in i R             1 1sin 3 sin 3 sin sin2 3 2 2 2 2lim 233 2 2sin sin2 2 n n n n n R                                                2 1 1lim 23 2 2n R          4 3Cx R  对题中圆盘:   2 1 2 3 44 c R x           2 2 1 2 3 4 1 2 3 4 4 4 4 3c R R Ry                 0cx  8 15c Ry   如图，一个圆盘半径为R，各处厚度一样， 在每个象限里，各处的密度也是均匀的，但不同象限里的密度则 不同，它们的密度之比为 ∶ ∶ ∶ ＝1∶ 2∶ 3∶ 4，求这圆 盘的质心位置． 1 2 3 4 1 y x 43 2 解:   2 1 2 3 4 4 4 3 R R         返回概要 2 h h 以静止水的质心为坐标原 点，建立如图所示坐标， O x y 当振动高度为Δh时，质心 坐标为： 1 1 1 2 2 2 3 2 2 2 6 2 3 2 4 L L L L L L Lh h h x L h hh                                              2 1 222 2 2 3 6 h h hh h L h L h y L h h h                        由上可得 2 2 6y h xL  O x y mg F回 yF mg x    质心沿抛物线做往复运 动,回复力为重力之分力:  2 2 2 6 x x xhmg L x       2 12mgh xL    质心做谐振,周期为 2 2 12T L hg  转动惯量♠ 量度刚体转动中惯性大小的物理量,等于刚体中每个 质点的质量mi与该质点到转轴的距离ri的平方的乘 积的总和. 2 i iJ m r  例讲 2J mr 2 1 lim n i in i J m r     2 2 1 lim 2 n n i m r r ri in n nr          2 3 4 1 1lim 2 n n i mr i n     21 2J mr 2 2 1 2 2 r rJ m  21 2J mr 21 2J m r 转轴 21 4J m r 2 2 4 12 m r m lJ   2 1 lim n i in i J m r     x y 0 R i i = 2 nn    = 2i i n    2 1 4 lim sin4 n in i m rn       2 2 2 2 2 1 1lim sin sin 2 sin sin2 2 n n i mr n                     n项21 2J m r 2 cJ J m d  miRi ri d x C y θi O  2 2 2 1 1 2 cos n n i i i i i i i J m r m R d dR         2 2 1 1 1 2 cos n n n i i i i i i i i i m R m d d m R          1 n i i i m x  0 m R 2 cJ J m d 由 2 2m R m R  22m R 2 2 1 12 lim 4 2 2 2 n n i m m lJ r in n n                2 2 2 3 1 lim4 4 n n i m r m l i n      2 2 4 12 m r m l M M2a 2a O 2 2 M aJ 圓   22cJ J M a 杆 C 2 1 2 lim 2 n c n i M a aJ ia n n         其 中 2 243 M a M a  OJ J J 圓 杆 229 6 M a 2 1 2 n x y z i i i J J J m r      对任意的刚体，任取直角三维坐标Oxyz，刚体对x、 y、z轴的转动惯量分别为Jx、Jy、Jz，则有  2 2 1 n x i i i i J m y z    x y z O xi yi zi ri mi  2 2 1 n y i i i i J m x z     2 2 1 n z i i i i J m x y     2 2 2 1 2 x y z n i i i i i J J J m x y z       2 ir 2 1 3 2 lim n i in i J m r     22mr 22 3J mr 球 壳 实 心 球 2 1 3 2 lim n i in i J m r     2 2 3 1 2 lim 4 4 / 3 n n i m r r ri in n nr                   2 4 5 1 16 lim n n i mr i n    22 5J mr 解: x x 已知:Jx=J0 0y xJ J J  y 2 02 i iJ m r  y O xJ  求: ? y xJ J  22 x i iJ m r   0xJ J  解: R Z1 Z2 Z４ Z３ 22 2x z i iJ J m r   2 3 4 2z i iJ J J m r    3 42 xJ J J  2 2 mR  22 2 4 12 m RmR  213 24x mRJ  Z 如图所示，质量为m的均匀圆柱体，截面半径 为R，长为2R．试求圆柱体绕通过质心及两底面边缘的转轴（如 图中的Z1、Z2）的转动惯量J． y xO 由正交轴定理:  2 2 A B i i iJ J m x y   由椭圆方程: 2 2 2 2 1x y A B   解: 2 2 2 2 i AA y B 2 2 2 2A B A B AJ J mA J B    2 2 2 ABJ AmA J B  椭圆细环的半长轴为A，半短轴为B， 质量为m（未必匀质），已知该环绕长轴的转动惯量为 JA，试求该环绕短轴的转动惯量JB． 2 2 1 n i i i J m r kma    转动惯量的表达式常表现为形式 m是刚体的质量，a是刚体相应的几何长度，只要确 定待定系数k，转动惯量问题便迎刃而解． OO a M 2 OOJ kMa  设 则有 2 2 24 4 2 4 4 M a M ak kMa                 1 12k  2 12OO MaJ   P Q O C 3 2 d 将立方体等分为边长为a/2的 八个小立方体，其中六个小 立方体体对角线到大立方体 体对角线距离 解: 2 6 2 63 ad a   22 2 2 2 68 2 8 2 8 6 m a m a m akma k k                                  1 6k  2 6PQJ ma 如图所示，匀质立方体的边长为a， 质量为m．试求该立方体绕对角线轴PQ的转动惯量J． O 描述转动状态的物理量♠ θ 0 lim t t       0 lim t t       a r  2 i i i i im v r mL r J      2 2 2 21 1 1 2 2 2i i ik im v m r JE      M Fd A M I M t   刚体的定轴转动与质点的直线运动♠ 　角动量原理　Mt＝Jωt－Jω0 动量定理 Ft＝m vt－m v0 (恒 力) 转动定律 M=J 牛顿运动定律　F＝ma 匀变速直线运动 匀速直线运动: s＝vt 加速度a 角速度 速度v 角位移　θ位移　s 刚体的定轴转动 质点的直线运动 0 lim t sv t     0 lim t t      0 lim t va t    角加速度 0 lim t t      匀角速转动: t  匀变速转动: 0tv v at  2 0 1 2S v t at  2 0 1 2t t    2 2 0 2tv v aS  0t t    2 2 0 2t     动能定理 　转动动能定理　2 2 0 1 1 2 2tFS mv mv  2 2 0 1 1 2 2tM J J    动量守恒定律 mv  恒量 角动量守恒定律 J  恒量 飞轮质量60 kg,直径d=0.50 m闸瓦 与轮间μ=0.4;飞轮质量分布在外层 圆周,要求在t=5 s内制动,求F力大小. 解: 2 21000 2 20s s60 5 3t         1000r / min  F0.50m 0.75m 对飞轮 2 215 kg m2 4 dJ m       fM J 其中 f N 2f dM N  对制动杆 F N f 0.5 1.25N F   5 2 F 100 NF  A B 质量为m的均匀细杆由竖直受一微扰倒下, 求夹角为θ时,质心速度及杆的角速度 B C 解:质心不受水平方向作用,做自由下落运动! 由机械能守恒:   2 21 11 cos2 2 2 lmg mv J     v vB vn 由相关速度: sin sin2n lv v      杆对质心的转动惯量: 2 2 1 lim 2 12 n n i m l l mlJ il n n            2 12 1 cos 1 3sin g l        2 3 1 cos sin1 3sinv g l     着地时,两杆瞬时转轴为A(B) 解: BA 由机械能守恒: 212 22 2 hmg J  其中各杆: 22 2 12 2 3 ml l mlJ m      cv l 2212 2 3 cvmlmgh l        則 3c hv g得 vc h 如图，两根等重的细杆AB及AC，在C点用铰链连接，放在光滑 水平面上，设两杆由图示位置无初速地开始运动，求铰链C着地时的速度． 轴心降低h过程中机械能守恒 解: B h v 21 2 Pmgh J  其中圆柱体对轴P的转动惯量 2 2 2 3 2 2P mr mrJ mr   P v r 2 3v gh T 由转动定律: Tr J 2 2 mr a r   mg T ma 由质心运动定律: 1 3T mg 如图，圆柱体A的质量为m，在其中部绕以细 绳，绳的一端B固定不动，圆柱体初速为零地下落，当其轴心降 低h时，求圆柱体轴心的速度及绳上的张力． 纯滚动时圆柱角速度由机械能守恒:解: vc0 ωc0 h 2 2 2 2 0 0 1 1 2 2 2 m rm gh J m r            20 4 3 gh r   与墙弹性碰撞,质心速度反向,角速度不变,此后受摩擦力作用 经时间t 达纯滚动: vc0 ωc0 vct ωct 由动量定理  0tf t m r r     由角动量定理  0c tfr t J       2 2 3 3t gh r   纯滚动后机械能守恒: 2 21 3 2 2 t m rm gh         9 hh  如图，实心圆 柱体从高度为h的斜坡上从静止纯 滚动地到达水平地面上，继续纯 滚动，与光滑竖直墙做完全弹性 碰撞后返回，经足够长的水平距 离后重新做纯滚动，并纯滚动地 爬上斜坡，设地面与圆柱体之间 的摩擦系数为μ，试求圆柱体爬坡 所能达到的高度h′. 由机械能守恒:解: 2 2 2 2 0 0 1 1( ) ( )2 2t tmgs I m v v     2 v s  又 2 2 0 2 2 2 4t mv v gs I m s      g 0 'tv v g t  2 2 4 mg g I m s     竖直方向匀加速下落! 如图，在一个固定的、竖直的螺杆上的一个 螺帽，螺距为s，螺帽的转动惯量为I，质量为m．假定螺帽与螺杆 间的摩擦系数为零，螺帽以初速度v0向下移动，螺帽竖直移动的 速度与时间有什么关系？这是什么样的运动？重力加速度为g． 解: vv R 1 2 v2 v R 1 1v 1v R 1 2v2 2v R ⑴完成弹性碰撞后设两球各经t1、t2达到纯滚动，质心速度为v1、v2， 对球1： 1 1 2 1 1 2 5 f t mv vmR vfR t R R           ， 1 2 7v v  对球2：  2 2 2 2 2 2 5 f t m v v vmRfR t R         2 5 7v v  在水平地面上有两个完全相同的均匀实心球，其一做 纯滚动，质心速度为v，另一静止不动，两球做完全弹性碰撞，因碰 撞时间很短，碰撞过程中摩擦力的影响可以不计．试求⑴碰后两球 达到纯滚动时的质心速度；⑵全部过程中损失的机械能的百分数． 续解 ⑵系统原机械能为 22 2 2 0 1 2 7 2 5 10 m r v m vE m r r               达到纯滚动后的机械能 2 22 21 7 2 5 29 2 5 7 7 70t mR v vE mvR R                  20 4149   則 % 读题 圆柱半径与小球半径分别以R、r表示 解:  vc mg f N 对球由质心运动定律有 ： 对球由转动定律： 2 cos cmvmg N R r     sinmg f m r   22 5fr mr   小球做纯滚动，摩擦力为静摩擦力，不做功，球的机械能守恒：    2 2 21 21 cos 2 5 cvmg R r mr mr r              2 sin7 mgf       10 1 coscos 7 mg R rmg N R r      17 10cos7 7N mg       小球做纯滚动必有 f N 2sin 17cos 10    0.7  45 45 如图所示，实心匀质小球静止在圆柱面顶点，受到微扰而自 由滚下，为了令小球在θ ≤45°范围内做纯滚动，求柱面与球间摩擦因数至少多大？ 解: 0 0c c c cmRv J mRv J     0 0 2 3c cv v R    即 达到纯滚时必有: cv R 纯滚时质心速度 0 0 3 2 5 5c cv v R  0c cv v gt 对质心:  0 02 5 ct v R g    0 0 2 3cv R若 > 0 0 2 3cv R若 <  2 cmR J  既滚又滑时与达到纯滚时对与地接触点O角动量守恒: 如图所示，半径为R的乒乓球，绕质心轴的转动惯量J＝ ，m 为乒乓球的质量，以一定的初始条件在粗糙的水平面上运动，开始时球的质心速度为vc0， 初角速度为ω0，两者的方向如图．已知乒乓球与地面间的摩擦系数为μ．试求乒乓球开始 做纯滚动所需的时间及纯滚动时的质心速度． 22 3 mR R vc0 ω0 O μ 设以某棱为轴转动历时Δt，角速度ωi→ωf，解: vi v f 30° 30° f N θ a 对质心由动量定理：  sin 30f iN t Ma      对刚体由动量矩定理：  cos30f if t Ma       cos30 sin30f ta N ta     25 12 f iMa    11 17f i 可得 211 121 17 2 9, 8s r s  則 时间短，忽略重力冲量及冲量矩 i f 如图所示，一个直、刚性的固体正六角棱柱，形状就像通常 的铅笔，棱柱的质量为M，密度均匀．横截面六边形每边长为a．六角棱柱相对于它的 中心轴的转动惯量I为 ．现令棱柱开始不均匀地滚下斜面．假设摩擦力足以阻止 任何滑动，并且一直接触斜面．某一棱刚碰上斜面之前的角速度为ωi，碰后瞬间角速度 为ωf，在碰撞前后瞬间的动能记为Eki和 Ekf，试证明ωf＝sωi， Ekf＝rE，并求出系数s 和r的值． 25 12 Ma ⑴碰后系统质心位置从杆中点右移 解: 2 m lx M m   x由质心系动量守恒：  0 cmv M m V  cV R 由角动量守恒： 2 0 2 12 2m C c l Ml lmv m V V        06 ( 4 ) mv M m l    得 2 l x    ⑵对瞬时转动中心有   4 6 M mR lM m   可得 cV m cV  mv R 6R lx  瞬时轴距杆右端 2 3 l cV 如图所示，光滑水平地面上静止地放着质量为M、长为l的均 匀细杆．质量为m的质点以垂直于杆的水平初速度v0与杆的一端做完全非弹性碰撞．试 求：⑴碰后系统质心的速度及绕质心的角速度；⑵实际的转轴（即静止点）位于何处？ 复摆♠ 在重力作用下绕水平轴在竖直面内做小角度摆 动的刚体称为复摆或物理摆． O C l 由机械能守恒关系可得   211 cos 2mgl J   对摆长l、质量m的理想单摆有    2 0 11 cos 2mgl m l   θ2J 2 0AJm m l       2 02 Jm l ml        2 0m l 2 0 0 ml J    2T J mgl  2 Jm m       解: A B C b a cＯ (b) 42cm 10cm (a) (c) A B C三种情况下的周期 相同，故有 2 2 0 0J ma J mc mga mgc   2 2 0 0J ma J mb mga mgb     0 0J mac c a    0J mac 0   0 0J mab b a   0 a b 2 2 2mac mcT mgc a c g    則 代入题给数据有: 1.03sT  形状适宜的金属丝衣架能在如图所示的平面里的几个平衡位置 附近做小振幅摆动．在位置(a)和位置(b)里，长边是水平的．其它两边等长．三 种情况下的振动周期都相等．试问衣架的质心位于何处？摆动周期是多少？ 先计算板对过C平行AB的轴的转动惯量 :解: 2 2 2 4 4 2 4 4 M d M dkMd k                 由 1 12k  2 12CJ M d B A  Mg C  O 等效摆长 2sin dl d 由复摆周期公式 2 JT Mgl  2 3T d g 2 2 3 Md Mgd  则 22 2 2 312AB M dM MdJ d       如图所示，矩形均匀薄片ABCD绕固定轴AB摆动，AB轴与竖直成， 薄片宽度AD=d，试求薄片做微小振动时的周期． 薄板原对悬点的转动惯量 解: 22 2 0 2 2 6 2 3 Ma MaJ M a        贴m后 2 22 3J Ma m x   振动周期相同，应有 0 ( ) ' J J Mgl M m gl   2 2 3x a C O m 2 2l a ' mx M ml Ml  'l 一个均匀的薄方板，质量为M，边长为a，固定 它的一个角点，使板竖直悬挂，板在自身的重力作用下，在自己的 平面内摆动．在穿过板的固定点的对角线上的什么位置（除去转动 轴处之外），贴上一个质点m，板的运动不会发生变化？已知对穿 过板中心而垂直于板的轴，板转动惯量 ． 21 6J Ma