九年级数学上册第四章图形的相似4探索三角形相似的条件第1课时利用两角判定三角形相似教学课件新版北师大版 21页

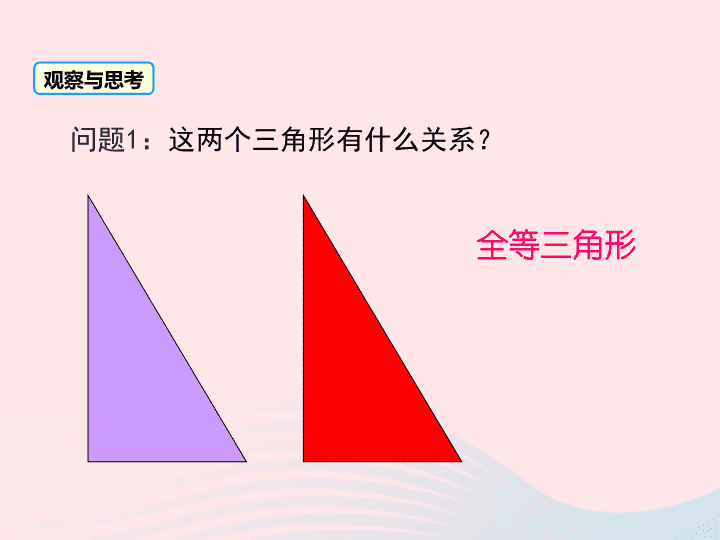
4.4 探索三角形相似的条件 第四章 图形的相似 第 1 课时 利用两角判定三角形相似 导入新课 讲授新课 当堂练习 课堂小结 1. 理解相似三角形的定义，掌握定义中的两个条件 . 2. 掌握相似三角形的判定定理 1. （重点） 3. 能熟练运用相似三角形的判定定理 1. （难点） 学习目标 问题 1 ： 这两个三角形有什么关系？ 观察与思考 全等三角形 那这样变化一下呢？ 相似三角形 相似三角形定义 ：我们把 三角 分别相等、 三边 成比例的两个三角形叫做相似三角形。 对应角 …… ？ 对应边 …… ？ 问题 2 相似多边形的定义是什么？那根据相似多边形的定义，你能说说什么叫相似三角形吗？ 全等是一种特殊的相似 定义 判定 方法 全等三角形 相似三角形 三角、三边对应相等的两个三角形全等 三角对应相等 , 三边对应成比例的两个三角形相似 角边角 A S A 角角边 A A S 边边边 S S S 边角边 S A S 斜边、直角边 H L 问题 3 三角形全等的性质和判定方法有哪些？ 需要 三个 等量条件 思考 全等是一种特殊的相似，那你猜想一下，判定两个三角形相似需要几个条件？ 问题 观察学生与老师的直角三角板相似吗？测量一下，得出你的猜想. 利用角的关系判定两个三角形相似 一 讲授新课 这两三角形是相似的 做一做： 画 △ ABC ，使 ∠ A =30°,∠ B =45° ，再画 △ A′B′C′ ，使 ∠ A′ = 30°,∠ B′ = 45°. 观察这两个三角形形状相同吗？你能证明 ∠ C =∠ C′ 吗？量出这两个三角形的三边，计算对应边是否对应成比例？由此你可以得出什么结论？ 两角分别相等的两个三角形相似 . 猜想： 由以上的探究写出利用角判定两个三角形全等的条件 . 探究猜想 已知：在 △ ABC 和 △ A′B′C′ 中， ∠ A =∠ A′ ，∠ B =∠ B′ . 求证：△ ABC ∽△ A′B′C ′ . B' A' D E C ' B A C 证明猜想 证明：在 △ A′B′C ′ 的边 A′B ′ 、 A′C ′ 上，分 别截取 A′D = AB ， A′E = AC ，连接 DE . ∵ A′D = AB ，∠ A =∠ A′ ， A′E = AC ， ∴△ A′DE ≌△ ABC ,∴∠ A′DE =∠ B ， 又∵∠ B′ =∠ B ，∴∠ A′DE =∠ B′ ， ∴ DE ∥ B′C′ ， ∴△ A′DE ∽△ A′B′C ′ ， ∴△ A′B′C ′ ∽△ ABC . B' A' D E C ' B A C 两角分别相等的两个三角形相似 . 归纳总结 A B C A' C' B' 用数学符号表示： ∵ ∠A=∠A' ， ∠ B=∠B' ∴ ΔABC ∽ ΔA'B'C' 相似三角形的判定定理： 注意： 对应点写在对应的位置 . 跟踪训练 ： 1.ΔABC 和 ΔDEF 中， ∠ A=40 ° ，∠ B=80 ° ， ∠ E=80 ° ， ∠ F=60 ° 。 ΔABC 与 ΔDEF_______ （“相似”或“不相似”） . ？ A C B 40 ° 80 ° F E D 80 ° 60 ° 2 . 有一个锐角相等的两直角三角形是否为相似 三角形？ 例 1 ： 如图， D , E 分别是△ ABC 的边 AB , AC 上的点， DE ∥ BC , AB =7 ， AD =5 ， DE =10 ，求 BC 的长 . 解：∵ DE ∥ BC , ∴∠ ADE =∠ B ，∠ AED =∠ C . ∴△ ADE ∽△ ABC ( 两角分别相等的两个三角形相似 ). ∴ ∴ BC =14 . B A D E C 典例精析 例 2 ： 如图， △ ABC 中， DE ∥ BC , EF ∥ AB . 求证： △ ADE ∽△ EFC . A E F B C D 解 : ∵ DE ∥ BC ， EF ∥ AB . ∴∠ AED ＝∠ C ， ∠ A ＝∠ FEC . ∴ △ ADE ∽△ EFC . （ 两角分别相等的两个三角形相似．） 例 3 ： 已知：如图，∠ 1=∠2=∠3 ， 求证：△ ABC ∽△ ADE ． 证明： ∵∠ BAC = ∠ 1+ ∠ DAC , ∠ DAE = ∠ 3+ ∠ DAC ， ∵ ∠ 1=∠3 ， ∴ ∠ BAC = ∠ DAE. ∵ ∠ C =180° －∠ 2 －∠ DOC ，∠ E =180° －∠ 3 －∠ AOE. 又 ∵ ∠ DOC = ∠ AOE （对顶角相等）， ∴ ∠ C = ∠ E. 在△ ABC 和△ ADE 中 ∠ BAC = ∠ DAE ， ∠ C = ∠ E ∴ △ ABC ∽△ ADE. 归纳总结 1. 已知： △ ABC 和 △ DEF 中，∠ A =40° ，∠ B =80 °,∠ E =80 ° , ∠ F =60 ° ．求证： △ ABC ∽ △ DEF. A F E C B D 证明：∵ 在 Δ ABC 中，∠ A =40 ° ，∠ B =80 ° ， ∴ ∠ C =180 ° －∠ A －∠ B =180 ° － 40 ° － 80 ° =60 °. ∵ 在 Δ DEF 中， ∠ E =80 ° ，∠ F =60 °. ∴ ∠ B =∠ E ，∠ C =∠ F . 　∴ △ ABC ∽ △ DEF （ 两角对应相等，两三角形相似） . 当堂练习 2. 如图，在 Rt△ ABC 中， ∠ C =90° .正方形 EFCD 的三个顶点 E ， F ， D 分别在边 AB ， BC ， AC 上.已知 AC = 7.5 ， BC = 5 ，求正方形的边长. 解： ∵四边形 EFCD 是正方形， ∴ ED ∥ BC , ED = DC = FC = EF . ∵∠ ADE =∠ ACB =90 °， ∠ AE D =∠ AB C . ∴ △ AED ∽ △ ABC . ∴ DE= 3 , 即正方形的边长为 3. 3. 如图，在等边三角形 ABC 中，边长为 10 ，点 D 在 BC 上， BD=6 ，∠ ADE=60° ， DE 交 AC 于 E. （ 1 ）求证：△ ABD ∽△ DCE. ∴∠ BAD= ∠ CDE, ∴△ ABD ∽△ DCE. 解：∵△ ABC 为等边三角形， ∴∠ B= ∠ C=60° ，∴∠ ADB+ ∠ BAD=120° ， 又∠ ADE=60° ，∴∠ ADB+ ∠ CDE=120° ， （ 2 ）求 CE 的长 . 6 10 4 解：∵ ABD ∽△ DCE ， ∴△ ABD ∽△ DCE ， ∴ CE=2.4. 利用两角判定三角形相似 定理：两角分别相等的两个三角形相似 课堂小结 相似三角形的判定定理 1 的运用