湘教版八年级数学下册 第4章 达标检测卷 19页

1 湘教版八年级数学下册 第 4 章 达标检测卷 (本试卷分第Ⅰ卷和第Ⅱ卷，考试时间：120 分钟，赋分：120 分) 第Ⅰ卷 (选择题 共 36 分) 一、选择题(本大题共 12 小题，每小题 3 分，共 36 分) 1．在利用太阳能热水器来加热水的过程中，热水器里的水温随所晒时间的长短 而变化，这个问题中因变量是( ) A．太阳光强弱 B．水的温度 C．所晒时间 D．热水器 2．函数 y＝ 4－3x 中自变量 x 的取值范围是( ) A．x<4 3 B．x≠4 3 C．x≤4 3 D．x≤0 3．在平面直角坐标系中，点 M，N 在同一个正比例函数图象上的是( ) A．M(2，－3)，N(－4，6) B．M(－2，3)，N(4，6) C．M(－2，－3)，N(4，－6) D．M(2，3)，N(－4，6) 4．有下列函数表达式：①y＝2x；②y＝2x＋11；③y＝3－x；④y＝x2＋2x＋3. 其中一次函数的个数有( ) A．1 个 B．2 个 C．3 个 D．4 个 5．把函数 y＝x 向上平移 3 个单位，下列在该平移后的直线上的点是( ) A．(2，2) B．(2，3) C．(2，4) D．(2，5) 6．如果一次函数 y＝kx＋b(k，b 是常数，k≠0)的图象经过第一、二、四象限， 那么 k，b 应满足的条件是( ) 2 A．k＞0 且 b＞0 B．k＜0 且 b＞0 C．k＞0 且 b＜0 D．k＜0 且 b＜0 7．一次函数的图象过点 P 5 3，0 且与函数 y＝3x＋5 的图象交于 y 轴上同一点， 则这个一次函数的表达式为( ) A．y＝3x＋5 B．y＝3x－5 C．y＝－3x－5 D．y＝－3x＋5 8．如果 P(2，m)，A(1，1)，B(4，0)三点在同一直线上，那么 m 的值为( ) A．2 B．－2 3 C．2 3 D．1 9．小张为自己已经用光话费的手机充值 100 元，他购买的服务是：20 元/月包接 听，主叫 0.2 元/分钟．这个月内，他手机所剩话费 y(元)与主叫时间 t(分钟)之 间的函数关系式是( ) A．y＝100－0.2t B．y＝80－0.2t C．y＝100＋0.2t D．y＝80＋0.2t 10．如图，一个长方体铁块放置在圆柱形水槽容器内，向容器内按一定的速度均 匀注水，60 秒后将容器内注满．容器内水面的高度 h(cm)与注水时间 t(s)之间的 函数关系图象大致是( ) A B C D 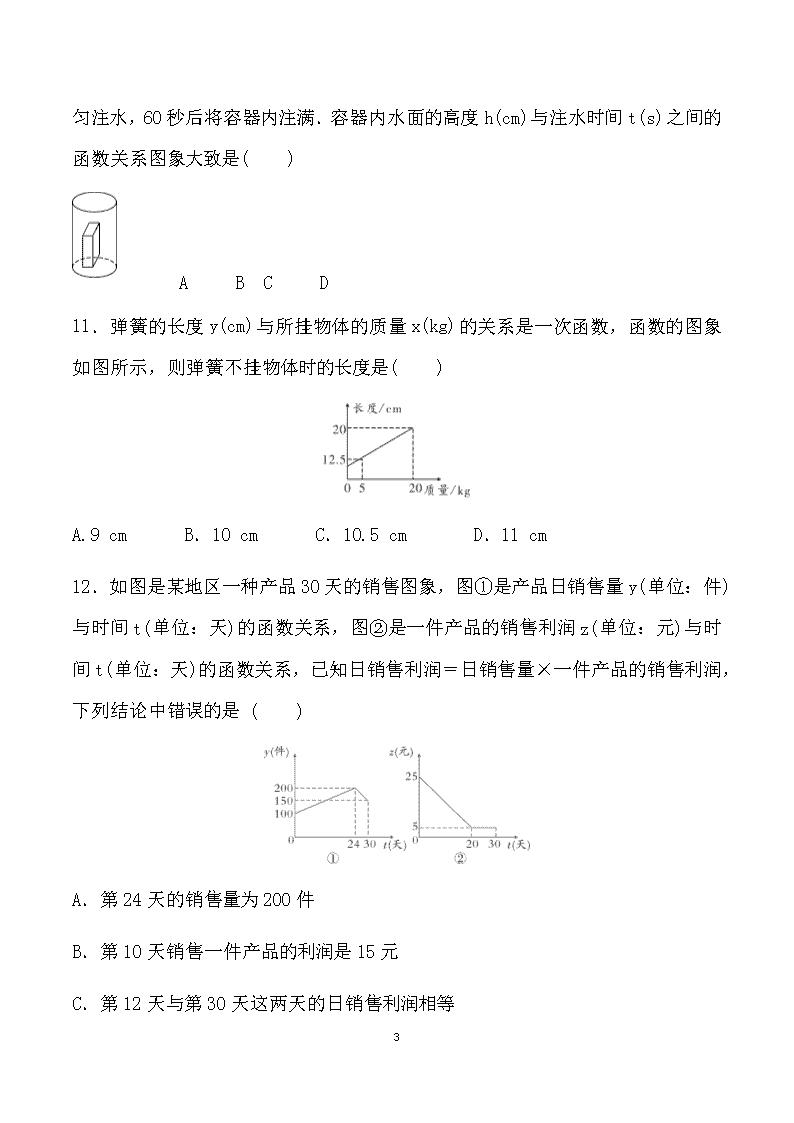11．弹簧的长度 y(cm)与所挂物体的质量 x(kg)的关系是一次函数，函数的图象 如图所示，则弹簧不挂物体时的长度是( ) 3 A.9 cm B．10 cm C．10.5 cm D．11 cm 12．如图是某地区一种产品 30 天的销售图象，图①是产品日销售量 y(单位：件) 与时间 t(单位：天)的函数关系，图②是一件产品的销售利润 z(单位：元)与时 间 t(单位：天)的函数关系，已知日销售利润＝日销售量×一件产品的销售利润， 下列结论中错误的是 ( ) A．第 24 天的销售量为 200 件 B．第 10 天销售一件产品的利润是 15 元 C．第 12 天与第 30 天这两天的日销售利润相等 D．第 30 天的日销售利润是 750 元 第Ⅱ卷 (非选择题 共 84 分) 二、填空题(本大题共 6 小题，每小题 3 分，共 18 分) 13．已知函数 f(x)＝ 3 1 2x＋1 ，那么 f(4)＝ ． 14．直线 y＝2x－6 与 y 轴的交点坐标是 ． 15．若直线 y＝ax＋b 与 x 轴交点的坐标是(－7，0)，则关于 x 的方程 ax＋b＝0 的解为 ． 16．若点 A(－2，y1)，B(1，y2)都在正比例函数 y＝－5x 的图象上，则 y1 y2(选 4 填“＞”“＜”或“＝”). 17．过点(－1，7)的一条直线与 x 轴，y 轴分别相交于点 A，B，且与直线 y＝－3 2 x ＋1 平行，则在线段 AB 上，横、纵坐标都是整数的点的坐标是_ ． 18．★直线 y＝k1x＋b1(k1＞0)与 y＝k2x＋b2(k2＜0)相交于点(－2，0)，且两直线 与 y 轴围成的三角形面积为 4，那么 b1－b2＝ ． 三、解答题(本大题共 8 小题，满分 66 分，解答应写出文字说明、证明过程或演 算步骤) 19．(本题满分 10 分)已知一次函数 y＝(3－m)x＋2m－9 的图象与 y 轴的负半轴 相交，y 随 x 的增大而减小，且 m 为整数． (1)求 m 的值； (2)当－1≤x≤2 时，求 y 的取值范围． 20．(本题满分 5 分)父亲告诉小明：“距离地面越远，温度越低．”并给小明出示 了下面的表格： 距离地面高度(千米) 0 1 2 3 4 5 温度(℃) 20 14 8 2 －4 －10 请根据上表，解答下列问题： (1)上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？ (2)如果用 h 表示距离地面的高度，用 t 表示温度，那么随着 h 的变化，t 是怎么 5 变化的？ (3)距离地面 5 千米的高空温度是多少？ (4)距离地面 6 千米的高空温度是多少？ 21．(本题满分 6 分)如图是小明散步过程中所走的路程 s(m)与步行时间 t(min) 的函数图象． (1)小明在散步过程中停留了多少时间？ (2)求小明散步过程中步行的平均速度； (3)在哪一段时间，小明是匀速步行的？在这一时间段，他步行的速度是多少？ 22．(本题满分 8 分)为了学生的身体健康，学校的课桌和椅子的高度是按一定的 关系科学设计的．小明对学校添置的一批课桌和椅子进行研究，发现它们可以根 据人的身高调节高度，于是测量了一套课桌和椅子相对应的四档的高度，数据如 6 下表： 档次 高度 第一档 第二档 第三档 第四档 椅子高度(cm) 37.0 40.0 42.0 45.0 课桌高度(cm) 70.0 74.8 78.0 82.8 (1)小明经过对数据的研究，发现课桌的高度 y(cm)是椅子的高度 x(cm)的一次函 数，请帮小明求出这个函数的关系式； (2)小明回家后，测量了家里自己的写字台和椅子，测得写字台的高度为 77 cm， 椅子的高度为 43.5 cm，请判断它们是否配套？为什么？ 23．(本题满分 8 分)如图，过点 A(4，0)的两条直线 l1，l2 分别交 y 轴于点 B，C， 其中点 B 在原点上方，点 C 在原点下方，已知 AB＝2 13 . (1)求点 B 的坐标； (2)若△ABC 的面积为 20，求直线 l2 的表达式． 7 24．(本题满分 8 分)某种水泥储存罐的容量为 25 m3，它有一个输入口和一个输 出口．从某时刻开始，只打开输入口，匀速向储存罐内注入水泥，3 min 后，再 打开输出口，匀速向运输车输出水泥，又经过 2.5 min 水泥储存罐注满．已知水 泥储存罐内的水泥量 y(m3)与时间 x(min)之间的函数图象如图所示． (1)求每分钟向储存罐内注入的水泥量； (2)当 3≤x≤5.5 时，求 y 与 x 之间的函数关系式； (3)水泥储存罐每分钟向运输车输出的水泥量是多少立方米？ 25．(本题满分 11 分)某物流公司引进 A，B 两种机器人用来搬运某种货物，这两 种机器人充满电后可以连续搬运 5 小时，A 种机器人于某日 0 时开始搬运，过了 1 小时，B 种机器人也开始搬运，如图，线段 OG 表示 A 种机器人的搬运量 yA(千 克)与时间 x(时)的函数图象，根据图象提供的信息，解答下列问题： (1)求 yB 关于 x 的函数表达式； (2)如果 A，B 两种机器人连续搬运 5 个小时，那么 B 种机器人比 A 种机器人多搬 运了多少千克？ 8 26．(本题满分 10 分)北流市某初中为了改善教师办公条件，计划采购 A，B 两种 型号的空调，已知采购 2 台 A 型空调和 1 台 B 型空调需要费用 24 000 元，3 台 A 型空调比 4 台 B 型空调的费用多 3 000 元． (1)求 A 型空调和 B 型空调每台各需多少元？ (2)若学校计划采购 A，B 两种型号空调共 30 台，B 型空调的台数不多于 A 型空调 台数的 2 倍，两型号空调的采购总费用不超过 218 000 元，该校共有哪几种采购 方案？ (3)在(2)的条件下，采用哪一种采购方案可使总费用最低，最低费用是多少元？ 9 参考答案 第Ⅰ卷 (选择题 共 36 分) 一、选择题(本大题共 12 小题，每小题 3 分，共 36 分) 1．在利用太阳能热水器来加热水的过程中，热水器里的水温随所晒时间的长短 而变化，这个问题中因变量是( B ) A．太阳光强弱 B．水的温度 C．所晒时间 D．热水器 2．函数 y＝ 4－3x 中自变量 x 的取值范围是( C ) A．x<4 3 B．x≠4 3 C．x≤4 3 D．x≤0 3．在平面直角坐标系中，点 M，N 在同一个正比例函数图象上的是( A ) A．M(2，－3)，N(－4，6) B．M(－2，3)，N(4，6) C．M(－2，－3)，N(4，－6) D．M(2，3)，N(－4，6) 4．有下列函数表达式：①y＝2x；②y＝2x＋11；③y＝3－x；④y＝x2＋2x＋3. 其中一次函数的个数有( C ) A．1 个 B．2 个 C．3 个 D．4 个 5．把函数 y＝x 向上平移 3 个单位，下列在该平移后的直线上的点是( D ) A．(2，2) B．(2，3) C．(2，4) D．(2，5) 6．如果一次函数 y＝kx＋b(k，b 是常数，k≠0)的图象经过第一、二、四象限， 那么 k，b 应满足的条件是( B ) A．k＞0 且 b＞0 B．k＜0 且 b＞0 10 C．k＞0 且 b＜0 D．k＜0 且 b＜0 7．一次函数的图象过点 P 5 3，0 且与函数 y＝3x＋5 的图象交于 y 轴上同一点， 则这个一次函数的表达式为( D ) A．y＝3x＋5 B．y＝3x－5 C．y＝－3x－5 D．y＝－3x＋5 8．如果 P(2，m)，A(1，1)，B(4，0)三点在同一直线上，那么 m 的值为( C ) A．2 B．－2 3 C．2 3 D．1 9．小张为自己已经用光话费的手机充值 100 元，他购买的服务是：20 元/月包接 听，主叫 0.2 元/分钟．这个月内，他手机所剩话费 y(元)与主叫时间 t(分钟)之 间的函数关系式是( B ) A．y＝100－0.2t B．y＝80－0.2t C．y＝100＋0.2t D．y＝80＋0.2t 10．如图，一个长方体铁块放置在圆柱形水槽容器内，向容器内按一定的速度均 匀注水，60 秒后将容器内注满．容器内水面的高度 h(cm)与注水时间 t(s)之间的 函数关系图象大致是( D ) A B C D 11．弹簧的长度 y(cm)与所挂物体的质量 x(kg)的关系是一次函数，函数的图象 如图所示，则弹簧不挂物体时的长度是( B ) 11 A.9 cm B．10 cm C．10.5 cm D．11 cm 12．如图是某地区一种产品 30 天的销售图象，图①是产品日销售量 y(单位：件) 与时间 t(单位：天)的函数关系，图②是一件产品的销售利润 z(单位：元)与时 间 t(单位：天)的函数关系，已知日销售利润＝日销售量×一件产品的销售利润， 下列结论中错误的是 ( C ) A．第 24 天的销售量为 200 件 B．第 10 天销售一件产品的利润是 15 元 C．第 12 天与第 30 天这两天的日销售利润相等 D．第 30 天的日销售利润是 750 元 第Ⅱ卷 (非选择题 共 84 分) 二、填空题(本大题共 6 小题，每小题 3 分，共 18 分) 13．已知函数 f(x)＝ 3 1 2x＋1 ，那么 f(4)＝__1__． 14．直线 y＝2x－6 与 y 轴的交点坐标是__(0，－6)__． 15．若直线 y＝ax＋b 与 x 轴交点的坐标是(－7，0)，则关于 x 的方程 ax＋b＝0 的解为__x＝－7__． 16．若点 A(－2，y1)，B(1，y2)都在正比例函数 y＝－5x 的图象上，则 y1__＞__y2(选 12 填“＞”“＜”或“＝”). 17．过点(－1，7)的一条直线与 x 轴，y 轴分别相交于点 A，B，且与直线 y＝－3 2 x ＋1 平行，则在线段 AB 上，横、纵坐标都是整数的点的坐标是__(3，1)或(1，4)__． 18．★直线 y＝k1x＋b1(k1＞0)与 y＝k2x＋b2(k2＜0)相交于点(－2，0)，且两直线 与 y 轴围成的三角形面积为 4，那么 b1－b2＝__4__． 三、解答题(本大题共 8 小题，满分 66 分，解答应写出文字说明、证明过程或演 算步骤) 19．(本题满分 10 分)已知一次函数 y＝(3－m)x＋2m－9 的图象与 y 轴的负半轴 相交，y 随 x 的增大而减小，且 m 为整数． (1)求 m 的值； 解：∵一次函数 y＝(3－m)x＋2m－9 的图象与 y 轴的负半轴相交，y 随 x 的增大 而减小， ∴ 3－m＜0， 2m－9＜0， 解得 3＜m＜4.5， ∵m 为整数，∴m＝4. (2)当－1≤x≤2 时，求 y 的取值范围． 解：由(1)知，m＝4，则该一次函数表达式为 y＝－x－1. ∵－1≤x≤2，∴－3≤－x－1≤0， 即 y 的取值范围是－3≤y≤0. 20．(本题满分 5 分)父亲告诉小明：“距离地面越远，温度越低．”并给小明出示 了下面的表格： 13 距离地面高度(千米) 0 1 2 3 4 5 温度(℃) 20 14 8 2 －4 －10 请根据上表，解答下列问题： (1)上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？ (2)如果用 h 表示距离地面的高度，用 t 表示温度，那么随着 h 的变化，t 是怎么 变化的？ (3)距离地面 5 千米的高空温度是多少？ (4)距离地面 6 千米的高空温度是多少？ 解：(1)上表反映了温度和距地面高度之间的关系，高度是自变量，温度是因变 量． (2)由表可知，每上升一千米，温度降低 6 ℃，可得表达式为 t＝20－6h. (3)由表可知，距地面 5 千米时，温度为－10 ℃. (4)将 t＝6 代入 h＝20－6t，可得 t＝20－36＝－16. 即距离地面 6 千米的高空温度是－16 ℃. 21．(本题满分 6 分)如图是小明散步过程中所走的路程 s(m)与步行时间 t(min) 的函数图象． (1)小明在散步过程中停留了多少时间？ (2)求小明散步过程中步行的平均速度； (3)在哪一段时间，小明是匀速步行的？在这一时间段，他步行的速度是多少？ 14 解∶(1)小明散步过程中停留的时间为 25－20＝5(min). (2)小明散步过程中步行的平均速度为 2 000÷50＝40(m/min). (3)在 25～50 min 这一段时间内，小明是匀速步行的，步行的速度为 (2 000－1 200)÷(50－25)＝32(m/min). 22．(本题满分 8 分)为了学生的身体健康，学校的课桌和椅子的高度是按一定的 关系科学设计的．小明对学校添置的一批课桌和椅子进行研究，发现它们可以根 据人的身高调节高度，于是测量了一套课桌和椅子相对应的四档的高度，数据如 下表： 档次 高度 第一档 第二档 第三档 第四档 椅子高度(cm) 37.0 40.0 42.0 45.0 课桌高度(cm) 70.0 74.8 78.0 82.8 (1)小明经过对数据的研究，发现课桌的高度 y(cm)是椅子的高度 x(cm)的一次函 数，请帮小明求出这个函数的关系式； (2)小明回家后，测量了家里自己的写字台和椅子，测得写字台的高度为 77 cm， 椅子的高度为 43.5 cm，请判断它们是否配套？为什么？ 解：(1)设桌高 y 与椅高 x 的关系式为 y＝kx＋b(k≠0)，依题意，得 15 70＝37k＋b， 74.8＝40k＋b， 解得 k＝1.6， b＝10.8. ∴桌高 y 与椅高 x 的关系式为 y＝1.6x＋10.8. (2)不配套． ∵当 x＝43.5 时，y＝1.6×43.5＋10.8＝80.4， 又∵80.4≠77， ∴它们不配套． 23．(本题满分 8 分)如图，过点 A(4，0)的两条直线 l1，l2 分别交 y 轴于点 B，C， 其中点 B 在原点上方，点 C 在原点下方，已知 AB＝2 13 . (1)求点 B 的坐标； 解：∵点 A(4，0)， ∴AO＝4. ∵∠AOB＝90°，AO＝4，AB＝2 13 ， ∴BO＝ 36 ＝6， ∴点 B 的坐标为(0，6). (2)若△ABC 的面积为 20，求直线 l2 的表达式． 16 解：∵△ABC 的面积为 20， ∴1 2 BC×AO＝20. ∴BC＝10.∵BO＝6，∴CO＝10－6＝4， ∴C(0，－4). 设 l2 的表达式为 y＝kx＋b，则 b＝－4， 0＝4k＋b， 解得 k＝1， b＝－4， ∴l2 的表达式为 y＝x－4. 24．(本题满分 8 分)某种水泥储存罐的容量为 25 m3，它有一个输入口和一个输 出口．从某时刻开始，只打开输入口，匀速向储存罐内注入水泥，3 min 后，再 打开输出口，匀速向运输车输出水泥，又经过 2.5 min 水泥储存罐注满．已知水 泥储存罐内的水泥量 y(m3)与时间 x(min)之间的函数图象如图所示． (1)求每分钟向储存罐内注入的水泥量； (2)当 3≤x≤5.5 时，求 y 与 x 之间的函数关系式； (3)水泥储存罐每分钟向运输车输出的水泥量是多少立方米？ 解：(1)每分钟向储存罐内注入的水泥量为 15÷3＝5(立方米). (2)设 y＝kx＋b(k≠0)， 17 把(3，15)，(5.5，25) 代入，得 3k＋b＝15， 5.5k＋b＝25， 解得 k＝4， b＝3， ∴当 3≤x≤5.5 时，y 与 x 之间的函数关系式为 y＝4x＋3. (3)输入输出同时打开时，水泥储存罐的水泥增加速度为 25－15 5.5－3 ＝4 立方米/分， 则每分钟输出量为 5－4＝1(立方米). 25．(本题满分 11 分)某物流公司引进 A，B 两种机器人用来搬运某种货物，这两 种机器人充满电后可以连续搬运 5 小时，A 种机器人于某日 0 时开始搬运，过了 1 小时，B 种机器人也开始搬运，如图，线段 OG 表示 A 种机器人的搬运量 yA(千 克)与时间 x(时)的函数图象，根据图象提供的信息，解答下列问题： (1)求 yB 关于 x 的函数表达式； (2)如果 A，B 两种机器人连续搬运 5 个小时，那么 B 种机器人比 A 种机器人多搬 运了多少千克？ 解：(1)设 yB 关于 x 的函数表达式为 yB＝kx＋b(k≠0)，将点(1，0)，(3，180)代入，得 18 k＋b＝0， 3k＋b＝180， 解得 k＝90， b＝－90. 所以 yB 关于 x 的函数表达式为 yB＝90x－90(1≤x≤6). (2)设 yA 关于 x 的表达式为 yA＝k1x. 根据题意，得 3k1＝180.解得 k1＝60，所以 yA＝60x. 当 x＝5 时，yA＝60×5＝300(千克)； x＝6 时，yB＝90×6－90＝450(千克). 450－300＝150(千克). 答：如果 A，B 两种机器人各连续搬运 5 小时，B 种机器人比 A 种机器人多搬运了 150 千克． 26．(本题满分 10 分)北流市某初中为了改善教师办公条件，计划采购 A，B 两种 型号的空调，已知采购 2 台 A 型空调和 1 台 B 型空调需要费用 24 000 元，3 台 A 型空调比 4 台 B 型空调的费用多 3 000 元． (1)求 A 型空调和 B 型空调每台各需多少元？ (2)若学校计划采购 A，B 两种型号空调共 30 台，B 型空调的台数不多于 A 型空调 台数的 2 倍，两型号空调的采购总费用不超过 218 000 元，该校共有哪几种采购 方案？ (3)在(2)的条件下，采用哪一种采购方案可使总费用最低，最低费用是多少元？ 解：(1)设 A 型空调每台需 x 元，B 型空调每台需 y 元，依题意，得 19 2x＋y＝24 000， 3x－4y＝3 000， 解得 x＝9 000， y＝6 000， 答：A 型空调每台需 9 000 元，B 型空调每台需 6 000 元． (2)设购买 A 型空调 m 台，则购买 B 型空调(30－m)台，依题意，得 30－m≤2m， 9 000m＋6000（30－m）≤218 000， 解得 10≤m≤122 3 . ∵m 为正整数，∴m 可以取 10，11，12， ∴共有三种采购方案， 方案 1：采购 A 型空调 10 台，B 型空调 20 台； 方案 2：采购 A 型空调 11 台，B 型空调 19 台； 方案 3：采购 A 型空调 12 台，B 型空调 18 台． (3)设总费用为 w 元． w＝9 000m＋6 000(30－m) ＝3 000m＋180 000 ∴当 m＝10 时，w 取得最小值， 此时 w＝210 000， ∴采用方案 1：采购 A 型空调 10 台，B 型空调 20 台可使总费用最低，最低费用 是 210 000 元．