2021年中考数学专题复习 专题25 正方形（教师版含解析） 36页

专题 25 正方形问题 1．正方形定义：有一组邻边相等并且有一个角是直角的平行四边形叫做正方形。 2．正方形的性质： (1)具有平行四边形、矩形、菱形的一切性质； (2)正方形的四个角都是直角，四条边都相等； (3)正方形的两条对角线相等，并且互相垂直平分，每一条对角线平分一组对角； (4)正方形是轴对称图形，有 4 条对称轴； (5)正方形的一条对角线把正方形分成两个全等的等腰直角三角形，两条对角线把正方形分成四个全等的小 等腰直角三角形； (6)正方形的一条对角线上的一点到另一条对角线的两端点的距离相等。 3．正方形的判定 判定一个四边形是正方形的主要依据是定义，途径有两种： 一是先证它是矩形，再证有一组邻边相等。即有一组邻边相等的矩形是正方形。 二是先证它是菱形，再证有一个角是直角。即有一个角是直角的菱形是正方形。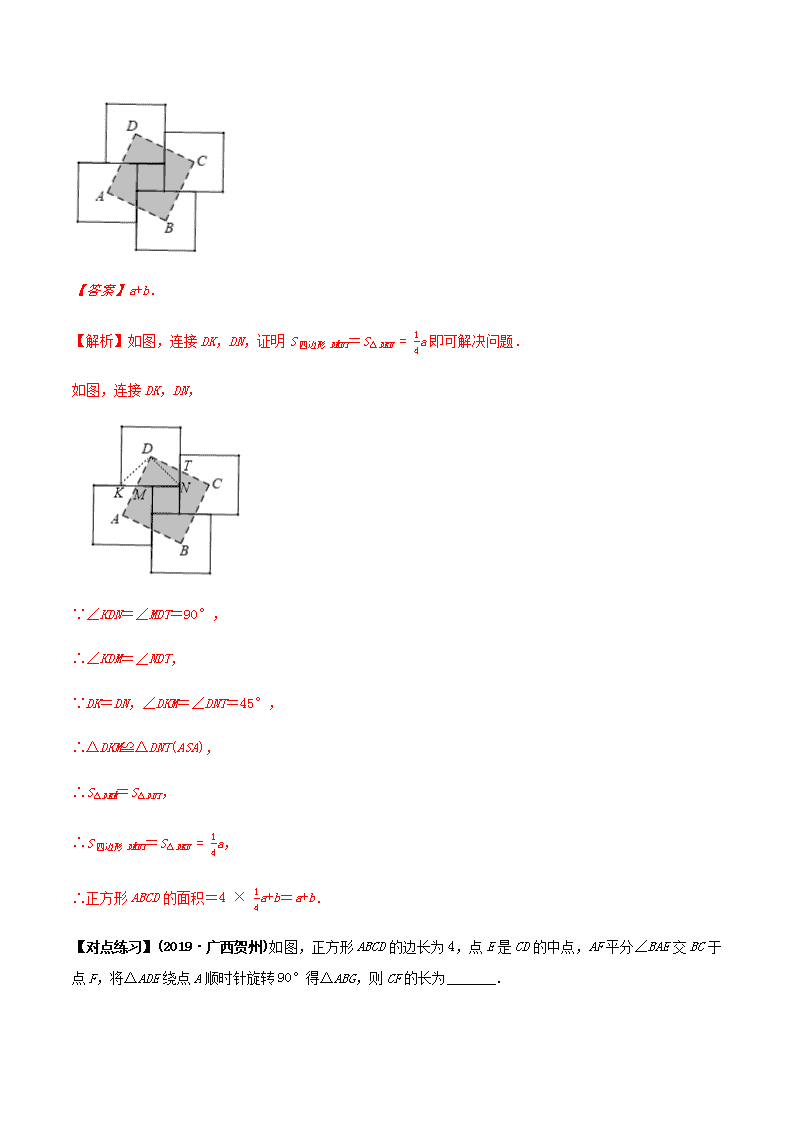 4．正方形的面积：设正方形边长为 a，对角线长为 b ，S= 2 2 2 ba  【例题 1】(2020•台州)用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案，每块大正方形 地砖面积为 a，小正方形地砖面积为 b，依次连接四块大正方形地砖的中心得到正方形 ABCD．则正方形 ABCD 的面积为 ．(用含 a，b 的代数式表示) 【答案】a+b． 【解析】如图，连接 DK，DN，证明 S 四边形 DMNT＝S△DKN a 即可解决问题． 如图，连接 DK，DN， ∵∠KDN＝∠MDT＝90°， ∴∠KDM＝∠NDT， ∵DK＝DN，∠DKM＝∠DNT＝45°， ∴△DKM≌△DNT(ASA)， ∴S△DKM＝S△DNT， ∴S 四边形 DMNT＝S△DKN a， ∴正方形 ABCD 的面积＝4× a+b＝a+b． 【对点练习】(2019·广西贺州)如图，正方形 ABCD 的边长为 4，点 E 是 CD 的中点，AF 平分∠BAE 交 BC 于 点 F，将△ADE 绕点 A 顺时针旋转 90°得△ABG，则 CF 的长为 ． 【答案】6﹣2 ． 【解析】作 FM⊥AD 于 M，FN⊥AG 于 N，如图，易得四边形 CFMD 为矩形，则 FM＝4， ∵正方形 ABCD 的边长为 4，点 E 是 CD 的中点， ∴DE＝2， ∴AE＝ ＝2 ， ∵△ADE 绕点 A 顺时针旋转 90°得△ABG， ∴AG＝AE＝2 ，BG＝DE＝2，∠3＝∠4，∠GAE＝90°，∠ABG＝∠D＝90°， 而∠ABC＝90°， ∴点 G 在 CB 的延长线上， ∵AF 平分∠BAE 交 BC 于点 F， ∴∠1＝∠2， ∴∠2+∠4＝∠1+∠3，即 FA 平分∠GAD， ∴FN＝FM＝4， ∵ AB•GF＝ FN•AG， ∴GF＝ ＝2 ， ∴CF＝CG﹣GF＝4+2﹣2 ＝6﹣2 ． 故答案为 6﹣2 ． 【例题 2】(2020•青岛)如图，在正方形 ABCD 中，对角线 AC 与 BD 交于点 O，点 E 在 CD 的延长线上，连接 AE，点 F 是 AE 的中点，连接 OF 交 AD 于点 G．若 DE＝2，OF＝3，则点 A 到 DF 的距离为 ． 【答案】 ． 【解析】根据正方形的性质得到 AO＝DO，∠ADC＝90°，求得∠ADE＝90°，根据直角三角形的性质得到 DF ＝AF＝EF AE，根据三角形中位线定理得到 FG DE＝1，求得 AD＝CD＝4，过 A 作 AH⊥DF 于 H，根据相似 三角形的性质和勾股定理即可得到结论． ∵在正方形 ABCD 中，对角线 AC 与 BD 交于点 O， ∴AO＝DO，∠ADC＝90°， ∴∠ADE＝90°， ∵点 F 是 AE 的中点， ∴DF＝AF＝EF AE， ∴OF 垂直平分 AD， ∴AG＝DG，∴FG DE＝1， ∵OF＝2，∴OG＝2， ∵AO＝CO，∴CD＝2OG＝4，∴AD＝CD＝4， 过 A 作 AH⊥DF 于 H，∴∠H＝∠ADE＝90°， ∵AF＝DF，∴∠ADF＝∠DAE，∴△ADH∽△AED， ∴ ， ∴AE 2 ， ∴ ，∴AH ， 即点 A 到 DF 的距离为 【对点练习】(2019 内蒙古包头)如图，在正方形 ABCD 中，AB＝1，点 E，F 分别在边 BC 和 CD 上，AE＝AF， ∠EAF＝60°，则 CF 的长是( ) A． B． C． ﹣1 D． 【答案】C 【解析】∵四边形 ABCD 是正方形， ∴∠B＝∠D＝∠BAD＝90°，AB＝BC＝CD＝AD＝1， 在 Rt△ABE 和 Rt△ADF 中， ， ∴Rt△ABE≌Rt△ADF(HL)， ∴∠BAE＝∠DAF， ∵∠EAF＝60°， ∴∠BAE+∠DAF＝30°， ∴∠DAF＝15°， 在 AD 上取一点 G，使∠GFA＝∠DAF＝15°，如图所示： ∴AG＝FG，∠DGF＝30°， ∴DF＝ FG＝ AG，DG＝ DF， 设 DF＝x，则 DG＝ x，AG＝FG＝2x， ∵AG+DG＝AD， ∴2x+ x＝1， 解得：x＝2﹣ ， ∴DF＝2﹣ ， ∴CF＝CD﹣DF＝1﹣(2﹣ )＝ ﹣1； 故选：C． 【例题 3】(2020•湘西州)如图，在正方形 ABCD 的外侧，作等边三角形 ADE，连接 BE，CE． (1)求证：△BAE≌△CDE； (2)求∠AEB 的度数． 【答案】见解析。 【解析】利用等边三角形的性质得到∠AD＝AE＝DE，∠EAD＝∠EDA＝60°，利用正方形的性质得到 AB＝AD ＝CD，∠BAD＝∠CDA＝90°，所以∠EAB＝∠EDC＝150°，然后根据“SAS”判定△BAE≌△CDE； 先证明 AB＝AE，然后根据等腰三角形的性质和三角形内角和计算∠ABE 的度数． (1)证明：∵△ADE 为等边三角形， ∴∠AD＝AE＝DE，∠EAD＝∠EDA＝60°， ∵四边形 ABCD 为正方形， ∴AB＝AD＝CD，∠BAD＝∠CDA＝90°， ∴∠EAB＝∠EDC＝150°， 在△BAE 和△CDE 中 ܤ ∠ ܤ ∠ ， ∴△BAE≌△CDE(SAS)； (2)∵AB＝AD，AD＝AE， ∴AB＝AE， ∴∠ABE＝∠AEB， ∵∠EAB＝150°， ∴∠ABE (180°﹣150°)＝15°． 【对点练习】(2019 湖南株洲)如图所示，已知正方形 OEFG 的顶点 O 为正方形 ABCD 对角线 AC、BD 的交点， 连接 CE、DG． (1)求证：△DOG≌△COE； (2)若 DG⊥BD，正方形 ABCD 的边长为 2，线段 AD 与线段 OG 相交于点 M，AM＝ 1 2 ，求正方形 OEFG 的边长． 【答案】(1)见解析；(2)2 ． 【解析】解： (1)∵正方形 ABCD 与正方形 OEFG，对角线 AC、BD ∴DO＝OC ∵DB⊥AC，∴∠DOA＝∠DOC＝90° ∵∠GOE＝90°，∴∠GOD+∠DOE＝∠DOE+∠COE＝90° ∴∠GOD＝∠COE ∵GO＝OE ∴在△DOG 和△COE 中 ∴△DOG≌△COE(SAS) (2)如图，过点 M 作 MH⊥DO 交 DO 于点 H ∵AM＝ 1 2 ，DA＝2，∴DM＝ ∵∠MDB＝45° ∴MH＝DH＝sin45°•DM＝ ，DO＝cos45°•DA＝ ∴HO＝DO﹣DH＝ ﹣ ＝ ∴在 Rt△MHO 中，由勾股定理得 MO＝ ＝ ＝ ∵DG⊥BD，MH⊥DO，∴MH∥DG ∴易证△OHM∽△ODG ∴ ＝ ＝ ＝ ，得 GO＝2 则正方形 OEFG 的边长为 2 ． 一、选择题 1．(2020•河南)如图，在△ABC 中，∠ACB＝90°，边 BC 在 x 轴上，顶点 A，B 的坐标分别为(﹣2，6)和(7， 0)．将正方形 OCDE 沿 x 轴向右平移，当点 E 落在 AB 边上时，点 D 的坐标为( ) A．( ，2) B．(2，2) C．( ，2) D．(4，2) 【答案】B 【解析】根据已知条件得到 AC＝6，OC＝2，OB＝7，求得 BC＝9，根据正方形的性质得到 DE＝OC＝OE＝2， 求得 O′E′＝O′C′＝2，根据相似三角形的性质得到 BO′＝3，于是得到结论． 如图，设正方形 D′C′O′E′是正方形 OCDE 沿 x 轴向右平移后的正方形， ∵顶点 A，B 的坐标分别为(﹣2，6)和(7，0)， ∴AC＝6，OC＝2，OB＝7， ∴BC＝9， ∵四边形 OCDE 是正方形， ∴DE＝OC＝OE＝2， ∴O′E′＝O′C′＝2， ∵E′O′⊥BC， ∴∠BO′E′＝∠BCA＝90°， ∴E′O′∥AC， ∴△BO′E′∽△BCA， ∴ ′ㄱ′ ܤㄱ′ ܤ ， ∴ ܤㄱ′ ， ∴BO′＝3， ∴OC′＝7﹣2﹣3＝2， ∴当点 E 落在 AB 边上时，点 D 的坐标为(2，2). 2．(2020•湖州)七巧板是我国祖先的一项卓越创造，流行于世界各地．由边长为 2 的正方形可以制作一副 中国七巧板或一副日本七巧板，如图 1 所示．分别用这两副七巧板试拼如图 2 中的平行四边形或矩形，则 这两个图形中，中国七巧板和日本七巧板能拼成的个数分别是( ) A．1 和 1 B．1 和 2 C．2 和 1 D．2 和 2 【答案】D 【解析】根据要求拼平行四边形矩形即可． 中国七巧板和日本七巧板能拼成的个数都是 2，如图所示： 故选：D． 3．(2020•温州)如图，在 Rt△ABC 中，∠ACB＝90°，以其三边为边向外作正方形，过点 C 作 CR⊥FG 于点 R， 再过点 C 作 PQ⊥CR 分别交边 DE，BH 于点 P，Q．若 QH＝2PE，PQ＝15，则 CR 的长为( ) A．14 B．15 C．8 D．6 【答案】A 【分析】如图，连接 EC，CH．设 AB 交 CR 于 J．证明△ECP∽△HCQ，推出 ，由 PQ＝15，可 得 PC＝5，CQ＝10，由 EC：CH＝1：2，推出 AC：BC＝1：2，设 AC＝a，BC＝2a，证明四边形 ABQC 是平行四 边形，推出 AB＝CQ＝10，根据 AC2+BC2＝AB2，构建方程求出 a 即可解决问题． 【解析】如图，连接 EC，CH．设 AB 交 CR 于 J． ∵四边形 ACDE，四边形 BCIH 都是正方形， ∴∠ACE＝∠BCH＝45°， ∵∠ACB＝90°，∠BCI＝90°， ∴∠ACE+∠ACB+∠BCH＝180°，∠ACB+∠BCI＝90° ∴B，C，D 共线，A，C，I 共线，E、C、H 共线， ∵DE∥AI∥BH， ∴∠CEP＝∠CHQ， ∵∠ECP＝∠QCH， ∴△ECP∽△HCQ， ∴ ， ∵PQ＝15， ∴PC＝5，CQ＝10， ∵EC：CH＝1：2， ∴AC：BC＝1：2，设 AC＝a，BC＝2a， ∵PQ⊥CR，CR⊥AB， ∴CQ∥AB， ∵AC∥BQ，CQ∥AB， ∴四边形 ABQC 是平行四边形， ∴AB＝CQ＝10， ∵AC2+BC2＝AB2， ∴5a2＝100， ∴a＝2 (负根已经舍弃)， ∴AC＝2 ，BC＝4 ， ∵ •AC•BC •AB•CJ， ∴CJ × 4， ∵JR＝AF＝AB＝10， ∴CR＝CJ+JR＝14 4．(2020•南京)如图，在平面直角坐标系中，点 P 在第一象限，⊙P 与 x 轴、y 轴都相切，且经过矩形 AOBC 的顶点 C，与 BC 相交于点 D．若⊙P 的半径为 5，点 A 的坐标是(0，8)．则点 D 的坐标是( ) A．(9，2) B．(9，3) C．(10，2) D．(10，3) 【答案】A 【分析】设⊙O 与 x、y 轴相切的切点分别是 F、E 点，连接 PE、PF、PD，延长 EP 与 CD 交于点 G，证明四边 形 PEOF 为正方形，求得 CG，再根据垂径定理求得 CD，进而得 PG、DB，便可得 D 点坐标． 【解析】设⊙O 与 x、y 轴相切的切点分别是 F、E 点，连接 PE、PF、PD，延长 EP 与 CD 交于点 G， 则 PE⊥y 轴，PF⊥x 轴， ∵∠EOF＝90°，∴四边形 PEOF 是矩形， ∵PE＝PF，PE∥OF，∴四边形 PEOF 为正方形， ∴OE＝PF＝PE＝OF＝5， ∵A(0，8)，∴OA＝8，∴AE＝8﹣5＝3， ∵四边形 OACB 为矩形，∴BC＝OA＝8，BC∥OA，AC∥OB， ∴EG∥AC， ∴四边形 AEGC 为平行四边形，四边形 OEGB 为平行四边形， ∴CG＝AE＝3，EG＝OB， ∵PE⊥AO，AO∥CB，∴PG⊥CD，∴CD＝2CG＝6，∴DB＝BC﹣CD＝8﹣6＝2， ∵PD＝5，DG＝CG＝3， ∴PG＝4，∴OB＝EG＝5+4＝9，∴D(9，2)． 5.(2020•天津)如图，四边形 OBCD 是正方形，O，D 两点的坐标分别是(0，0)，(0，6)，点 C 在第一象限， 则点 C 的坐标是( ) A．(6，3) B．(3，6) C．(0，6) D．(6，6) 【答案】D 【解析】利用正方形的性质求出 OB，BC，CD 即可． ∵四边形 OBCD 是正方形， ∴OB＝BC＝CD＝OD，∠CDO＝∠CBO＝90°， ∵O，D 两点的坐标分别是(0，0)，(0，6)， ∴OD＝6， ∴OB＝BC＝CD＝6， ∴C(6，6)． 二、填空题 6．(2020•连云港)如图，将 5 个大小相同的正方形置于平面直角坐标系中，若顶点 M、N 的坐标分别为(3， 9)、(12，9)，则顶点 A 的坐标为 ． 【答案】(15，3)． 【解析】由图形可得 MN∥x 轴，MN＝9，BN∥y 轴，可求正方形的边长，即可求解．如图， ∵顶点 M、N 的坐标分别为(3，9)、(12，9)， ∴MN∥x 轴，MN＝9，BN∥y 轴， ∴正方形的边长为 3， ∴BN＝6， ∴点 B(12，3)， ∵AB∥MN， ∴AB∥x 轴， ∴点 A(15，3) 7．(2020•绍兴)如图 1，直角三角形纸片的一条直角边长为 2，剪四块这样的直角三角形纸片，把它们按图 2 放入一个边长为 3 的正方形中(纸片在结合部分不重叠无缝隙)，则图 2 中阴影部分面积为 ． 【答案】4 ． 【解析】根据题意和图形，可以得到直角三角形的一条直角边的长和斜边的长，从而可以得到直角三角形 的另一条直角边长，再根据图形，可知阴影部分的面积是四个直角三角形的面积，然后代入数据计算即可．由 题意可得， 直角三角形的斜边长为 3，一条直角边长为 2， 故直角三角形的另一条直角边长为： ， 故阴影部分的面积是： × × 4 8．(2020•天水)如图，将正方形 OEFG 放在平面直角坐标系中，O 是坐标原点，点 E 的坐标为(2，3)，则点 F 的坐标为 ． 【答案】(﹣1，5)． 【解析】结合全等三角形的性质可以求得点 G 的坐标，再由正方形的中心对称的性质求得点 F 的坐标． 如图，过点 E 作 x 轴的垂线 EH，垂足为 H．过点 G 作 x 轴的垂线 GM，垂足为 M，连接 GE、FO 交于点 O′． ∵四边形 OEFG 是正方形， ∴OG＝EO，∠GOM＝∠OEH，∠OGM＝∠EOH， 在△OGM 与△EOH 中， ∠ ㄱth ∠ ㄱ ㄱt ㄱ ∠ tㄱh ∠ ㄱ∴△OGM≌△EOH(ASA) ∴GM＝OH＝2，OM＝EH＝3， ∴G(﹣3，2)． ∴O′( ， )． ∵点 F 与点 O 关于点 O′对称， ∴点 F 的坐标为 (﹣1，5)． 9．(2020•德州)如图，在矩形 ABCD 中，AB 2，AD ．把 AD 沿 AE 折叠，使点 D 恰好落在 AB 边上 的 D′处，再将△AED′绕点 E 顺时针旋转α，得到△A'ED″，使得 EA′恰好经过 BD′的中点 F．A′D″交 AB 于点 G，连接 AA′．有如下结论：①A′F 的长度是 2；②弧 D'D″的长度是 π；③△A′AF≌△A′ EG；④△AA′F∽△EGF．上述结论中，所有正确的序号是 ． 【答案】①②④． 【解析】∵把 AD 沿 AE 折叠，使点 D 恰好落在 AB 边上的 D′处， ∴∠D＝∠AD'E＝90°＝∠DAD'，AD＝AD'， ∴四边形 ADED'是矩形， 又∵AD＝AD' ， ∴四边形 ADED'是正方形， ∴AD＝AD'＝D'E＝DE ，AE AD ，∠EAD'＝∠AED'＝45°， ∴D'B＝AB﹣AD'＝2， ∵点 F 是 BD'中点， ∴D'F＝1， ∴EF ′ ′ 2， ∵将△AED′绕点 E 顺时针旋转α， ∴AE＝A'E ，∠D'ED''＝α，∠EA'D''＝∠EAD'＝45°， ∴A'F 2，故①正确； ∵tan∠FED' ′ ′ ， ∴∠FED'＝30° ∴α＝30°+45°＝75°， ∴弧 D'D″的长度 °× × 香 ° π，故②正确； ∵AE＝A'E，∠AEA'＝75°， ∴∠EAA'＝∠EA'A＝52.5°， ∴∠A'AF＝7.5°， ∵∠AA'F≠∠EA'G，∠AA'E≠∠EA'G，∠AFA'＝120°≠∠EA'G， ∴△AA'F 与△A'GE 不全等，故③错误； ∵D'E＝D''E，EG＝EG， ∴Rt△ED'G≌Rt△ED''G(HL)， ∴∠D'GE＝∠D''GE， ∵∠AGD''＝∠A'AG+∠AA'G＝105°， ∴∠D'GE＝52.5°＝∠AA'F， 又∵∠AFA'＝∠EFG， ∴△AFA'∽△EFG，故④正确， 故答案为：①②④． 10．(2020•攀枝花)如图，在边长为 4 的正方形 ABCD 中，点 E、F 分别是 BC、CD 的中点，DE、AF 交于点 G， AF 的中点为 H，连接 BG、DH．给出下列结论： ①AF⊥DE；②DG 香 ；③HD∥BG；④△ABG∽△DHF． 其中正确的结论有 ．(请填上所有正确结论的序号) 【解析】故答案为：①④． 【分析】证明△ADF≌△DCE，再利用全等三角形的性质结合余角的性质得到∠DGF＝90°，可判断①，再利 用三角形等积法 AD×DF÷AF 可算出 DG，可判断②；再证明∠HDF＝∠HFD＝∠BAG，求出 AG，DH，HF，可判 定△ABG～△DHF，可判断④；通过 AB≠AG，得到∠ABG 和∠AGB 不相等，则∠AGB≠∠DHF，可判断③． 【解析】∵四边形 ABCD 为正方形， ∴∠ADC＝∠BCD＝90°，AD＝CD， ∵E 和 F 分别为 BC 和 CD 中点， ∴DF＝EC＝2， ∴△ADF≌△DCE(SAS)， ∴∠AFD＝∠DEC，∠FAD＝∠EDC， ∵∠EDC+∠DEC＝90°， ∴∠EDC+∠AFD＝90°， ∴∠DGF＝90°，即 DE⊥AF，故①正确； ∵AD＝4，DF CD＝2， ∴AF ， ∴DG＝AD×DF÷AF ，故②错误； ∵H 为 AF 中点， ∴HD＝HF AF ， ∴∠HDF＝∠HFD， ∵AB∥DC， ∴∠HDF＝∠HFD＝∠BAG， ∵AG t 香 ，AB＝4， ∴ ܤ ܤ t ， ∴△ABG～△DHF，故④正确； ∴∠ABG＝∠DHF，而 AB≠AG， 则∠ABG 和∠AGB 不相等， 故∠AGB≠∠DHF， 故 HD 与 BG 不平行，故③错误。 11．(2020•咸宁)如图，四边形 ABCD 是边长为 2 的正方形，点 E 是边 BC 上一动点(不与点 B，C 重合)，∠ AEF＝90°，且 EF 交正方形外角的平分线 CF 于点 F，交 CD 于点 G，连接 AF，有下列结论： ①△ABE∽△ECG； ②AE＝EF； ③∠DAF＝∠CFE； ④△CEF 的面积的最大值为 1． 其中正确结论的序号是 ．(把正确结论的序号都填上) 【解析】①②③． 【分析】①由∠AEB+∠CEG＝∠AEB+∠BAE 得∠BAE＝∠CEG，再结合两直角相等得△ABE∽△ECG； ②在 BA 上截取 BM＝BE，易得△BEM 为等腰直角三角形，则∠BME＝45°，所以∠AME＝135°，再利用等角 的余角相等得到∠BAE＝∠FEC，于是根据“ASA”可判断△AME≌△ECF，则根据全等三角形的性质可对②进 行判断； ③由∠MAE+∠DAF＝45°，∠CEF+∠CFE＝45°，可得出∠DAF 与∠CFE 的大小关系，便可对③判断； ④设 BE＝x，则 BM＝x，AM＝AB﹣BM＝4﹣x，利用三角形面积公式得到 S△AME •x•(2﹣x)，则根据二次函数 的性质可得 S△AME 的最大值，便可对④进行判断． 【解析】①∵四边形 ABCD 是正方形， ∴∠B＝∠ECG＝90°， ∵∠AEF＝90°， ∴∠AEB+∠CEG＝∠AEB+∠BAE， ∴∠BAE＝∠CEG， ∴△ABE∽△ECG， 故①正确； ②在 BA 上截取 BM＝BE，如图 1， ∵四边形 ABCD 为正方形， ∴∠B＝90°，BA＝BC， ∴△BEM 为等腰直角三角形， ∴∠BME＝45°， ∴∠AME＝135°， ∵BA﹣BM＝BC﹣BE， ∴AM＝CE， ∵CF 为正方形外角平分线， ∴∠DCF＝45°， ∴∠ECF＝135°， ∵∠AEF＝90°， ∴∠AEB+∠FEC＝90°， 而∠AEB+∠BAE＝90°， ∴∠BAE＝∠FEC， 在△AME 和△ECF 中 ∠ h ∠ h ∠ h ∠ ， ∴△AME≌△ECF， ∴AE＝EF， 故②正确； ③∵AE＝EF，∠AEF＝90°， ∴∠EAF＝45°， ∴∠BAE+∠DAF＝45°， ∵∠BAE+∠CFE＝∠CEF+∠CFE＝45°， ∴∠DAF＝∠CFE， 故③正确； ④设 BE＝x，则 BM＝x，AM＝AB﹣BM＝4﹣x， S△ECF＝S△AME •x•(2﹣x) (x﹣1)2 ， 当 x＝1 时，S△ECF 有最大值 ， 故④错误． 12．(2020•河南)如图，在边长为 2 的正方形 ABCD 中，点 E，F 分别是边 AB，BC 的中点，连接 EC，FD， 点 G，H 分别是 EC，FD 的中点，连接 GH，则 GH 的长度为 ． 【解析】1． 【分析】设 DF，CE 交于 O，根据正方形的性质得到∠B＝∠DCF＝90°，BC＝CD＝AB，根据线段中点的定义 得到 BE＝CF，根据全等三角形的性质得到 CE＝DF，∠BCE＝∠CDF，求得 DF⊥CE，根据勾股定理得到 CE＝ DF ，点 G，H 分别是 EC，FD 的中点，根据射影定理即可得到结论． 【解析】设 DF，CE 交于 O， ∵四边形 ABCD 是正方形， ∴∠B＝∠DCF＝90°，BC＝CD＝AB， ∵点 E，F 分别是边 AB，BC 的中点， ∴BE＝CF， ∴△CBE≌△DCF(SAS)， ∴CE＝DF，∠BCE＝∠CDF， ∵∠CDF+∠CFD＝90°， ∴∠BCE+∠CFD＝90°， ∴∠COF＝90°， ∴DF⊥CE， ∴CE＝DF ， ∵点 G，H 分别是 EC，FD 的中点， ∴CG＝FH ， ∵∠DCF＝90°，CO⊥DF， ∴CF2＝OF•DF， ∴OF ， ∴OH ，OD ， ∵OC2＝OF•OD， ∴OC × ， ∴OG＝CG﹣OC ， ∴HG ㄱt ㄱ 1 三、解答题 13．(2020•遵义)如图，在边长为 4 的正方形 ABCD 中，点 E 为对角线 AC 上一动点(点 E 与点 A、C 不重合)， 连接 DE，作 EF⊥DE 交射线 BA 于点 F，过点 E 作 MN∥BC 分别交 CD、AB 于点 M、N，作射线 DF 交射线 CA 于 点 G． (1)求证：EF＝DE； (2)当 AF＝2 时，求 GE 的长． 【答案】见解析。 【分析】(1)要证明 EF＝DE，只要证明△DME≌△ENF 即可，然后根据题目中的条件和正方形的性质，可以 得到△DME≌△ENF 的条件，从而可以证明结论成立； (2)根据勾股定理和三角形相似，可以得到 AG 和 CG、CE 的长，然后即可得到 GE 的长． 【解答】(1)证明：∵四边形 ABCD 是正方形，AC 是对角线， ∴∠ECM＝45°， ∵MN∥BC，∠BCM＝90°， ∴∠NMC+∠BCM＝180°，∠MNB+∠B＝180°， ∴∠NMC＝90°，∠MNB＝90°， ∴∠MEC＝∠MCE＝45°，∠DME＝∠ENF＝90°， ∴MC＝ME， ∵CD＝MN， ∴DM＝EN， ∵DE⊥EF，∠EDM+∠DEM＝90°， ∴∠DEF＝90°， ∴∠DEM+∠FEN＝90°， ∴∠EDM＝∠FEN， 在△DME 和△ENF 中 ∠ h ∠ h h h ∠ h ∠ h ， ∴△DME≌△ENF(ASA)， ∴EF＝DE； (2)如图 1 所示，由(1)知，△DME≌△ENF， ∴ME＝NF， ∵四边形 MNBC 是矩形， ∴MC＝BN， 又∵ME＝MC，AB＝4，AF＝2， ∴BN＝MC＝NF＝1， ∵∠EMC＝90°， ∴CE ， ∵AF∥CD， ∴△DGC∽△FGA， ∴ t t ， ∴ t t ， ∵AB＝BC＝4，∠B＝90°， ∴AC＝4 ， ∵AC＝AG+GC， ∴AG ，CG 香 ， ∴GE＝GC﹣CE 香 ； 如图 2 所示， 同理可得，FN＝BN， ∵AF＝2，AB＝4， ∴AN＝1， ∵AB＝BC＝4，∠B＝90°， ∴AC＝4 ， ∵AF∥CD， ∴△GAF∽△GCD， ∴ t t ， 即 t t ， 解得，AG＝4 ， ∵AN＝NE＝1，∠ENA＝90°， ∴AE ， ∴GE＝GA+AE＝5 ． 14．(2019 湖南湘西州)如图，在正方形 ABCD 中，点 E，F 分别在边 CD，AD 上，且 AF ＝CE． (1)求证：△ABF≌△CBE； (2)若 AB＝4，AF＝1，求四边形 BEDF 的面积． 【答案】(1)见解析；(2)12． 【解答】(1)在△ABF 和△CBE 中 ， ∴△ABF≌△CBE(SAS)； (2)由已知可得正方形 ABCD 面积为 16， △ABF 面积＝△CBE 面积＝ 1 2 ×4×1＝2． 所以四边形 BEDF 的面积为 16﹣2×2＝12． 15.(2020 湖北仙桃模拟)如图，E，F 分别是正方形 ABCD 的边 CB，DC 延长线上的点，且 BE＝CF，过点 E 作 EG∥BF，交正方形外角的平分线 CG 于点 G，连接 GF．求证： (1)AE⊥BF； (2)四边形 BEGF 是平行四边形． 【答案】见解析。 【解析】由 SAS 证明△ABE≌△BCF 得出 AE＝BF，∠BAE＝∠CBF，由平行线的性质得出∠CBF＝∠CEG，证出 AE⊥EG，即可得出结论；延长 AB 至点 P，使 BP＝BE，连接 EP，则 AP＝CE，∠EBP＝90°，证明△APE≌△ ECG 得出 AE＝EG，证出 EG＝BF，即可得出结论． 证明：(1)∵四边形 ABCD 是正方形， ∴AB＝BC，∠ABC＝∠BCD＝90°， ∴∠ABE＝∠BCF＝90°， 在△ABE 和△BCF 中， ， ∴△ABE≌△BCF(SAS)， ∴AE＝BF，∠BAE＝∠CBF， ∵EG∥BF，∴∠CBF＝∠CEG， ∵∠BAE+∠BEA＝90°，∴∠CEG+∠BEA＝90°， ∴AE⊥EG，∴AE⊥BF； (2)延长 AB 至点 P，使 BP＝BE，连接 EP，如图所示： 则 AP＝CE，∠EBP＝90°，∴∠P＝45°， ∵CG 为正方形 ABCD 外角的平分线，∴∠ECG＝45°，∴∠P＝∠ECG， 由(1)得∠BAE＝∠CEG， 在△APE 和△ECG 中， ， ∴△APE≌△ECG(ASA)，∴AE＝EG， ∵AE＝BF，∴EG＝BF， ∵EG∥BF，∴四边形 BEGF 是平行四边形． 16．(2019•山东泰安)如图，四边形 ABCD 是正方形，△EFC 是等腰直角三角形，点 E 在 AB 上，且∠CEF＝90°， FG⊥AD，垂足为点 C． (1)试判断 AG 与 FG 是否相等？并给出证明； (2)若点 H 为 CF 的中点，GH 与 DH 垂直吗？若垂直，给出证明；若不垂直，说明理由． 【答案】见解析。 【解析】过点 F 作 FM⊥AB 交 BA 的延长线于点 M，可证四边形 AGFM 是矩形，可得 AG＝MF，AM＝FG，由“AAS” 可证△EFM≌△CEB，可得 BE＝MF，ME＝BC＝AB，可得 BE＝MA＝MF＝AG＝FG； 延长 GH 交 CD 于点 N，由平行线分线段成比例可得 ，且 CH＝FH，可得 GH＝HN，NC＝FG，即 可求 DG＝DN，由等腰三角形的性质可得 DH⊥HG． (1)AG＝FG， 理由如下：如图，过点 F 作 FM⊥AB 交 BA 的延长线于点 M ∵四边形 ABCD 是正方形 ∴AB＝BC，∠B＝90°＝∠BAD ∵FM⊥AB，∠MAD＝90°，FG⊥AD ∴四边形 AGFM 是矩形,∴AG＝MF，AM＝FG， ∵∠CEF＝90°， ∴∠FEM+∠BEC＝90°，∠BEC+∠BCE＝90° ∴∠FEM＝∠BCE，且∠M＝∠B＝90°，EF＝EC ∴△EFM≌△CEB(AAS) ∴BE＝MF，ME＝BC∴ME＝AB＝BC ∴BE＝MA＝MF∴AG＝FG， (2)DH⊥HG 理由如下：如图，延长 GH 交 CD 于点 N， ∵FG⊥AD，CD⊥AD ∴FG∥CD ∴ ，且 CH＝FH， ∴GH＝HN，NC＝FG，∴AG＝FG＝NC 又∵AD＝CD， ∴GD＝DN，且 GH＝HN，∴DH⊥GH 17.(2019•四川省凉山州)如图，正方形 ABCD 的对角线 AC、BD 相交于点 O，E 是 OC 上一点，连接 EB．过点 A 作 AM⊥BE，垂足为 M，AM 与 BD 相交于点 F．求证：OE＝OF． 【答案】见解析。 【解析】根据正方形的性质对角线垂直且平分，得到 OB＝OA，根据 AM⊥BE，即可得出∠MEA+∠MAE＝90° ＝∠AFO+∠MAE，从而证出 Rt△BOE≌Rt△AOF，得到 OE＝OF． 证明：∵四边形 ABCD 是正方形． ∴∠BOE＝∠AOF＝90°，OB＝OA． 又∵AM⊥BE， ∴∠MEA+∠MAE＝90°＝∠AFO+∠MAE， ∴∠MEA＝∠AFO． ∴△BOE≌△AOF(AAS)． ∴OE＝OF．