2020-2021学年浙江省温州市南浦实验中学九年级（上）期末数学试卷 解析版 29页

2020-2021 学年浙江省温州市南浦实验中学九年级（上）期末数 学试卷 一、选择题（本题有 10 小题，每小题 4 分，共 40 分.每小题只有一个选项是正确的，不选、 多选、错选均不给分） 1．若 ，则 的值等于（ ） A． B． C． D． 2． ⊙ O 的半径为 4cm，若点 P 到圆心的距离为 3cm，点 P 在（ ） A．圆内 B．圆上 C．圆外 D．无法确定 3．二次函数 y＝x2﹣1 的图象与 y 轴的交点坐标是（ ） A．（0，1） B．（1，0） C．（﹣1，0） D．（0，﹣1） 4．若一个圆内接正多边形的内角是 108°，则这个多边形是（ ） A．正五边形 B．正六边形 C．正八边形 D．正十边形 5．一个不透明的盒子里有 n 个除颜色外其他完全相同的小球，其中有 9 个黄球．每次摸球 前先将盒子里的球摇匀，任意摸出一个球记下颜色后再放回盒子，通过大量重复摸球实 验后发现，摸到黄球的频率稳定在 30%，那么估计盒子中小球的个数 n 为（ ） A．20 B．24 C．28 D．30 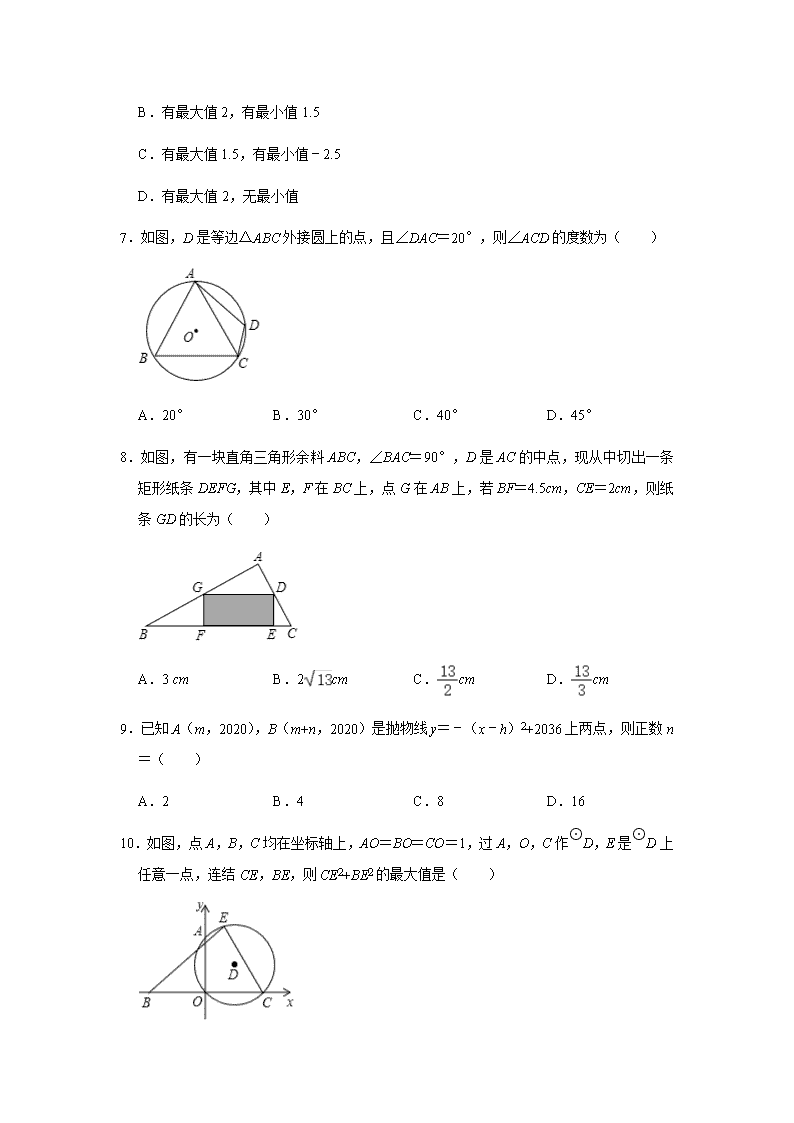6．已知二次函数的图象（0≤x≤4）如图，关于该函数在所给自变量的取值范围内，下列说 法正确的是（ ） A．有最大值 2，有最小值﹣2.5 B．有最大值 2，有最小值 1.5 C．有最大值 1.5，有最小值﹣2.5 D．有最大值 2，无最小值 7．如图，D 是等边△ABC 外接圆上的点，且∠DAC＝20°，则∠ACD 的度数为（ ） A．20° B．30° C．40° D．45° 8．如图，有一块直角三角形余料 ABC，∠BAC＝90°，D 是 AC 的中点，现从中切出一条 矩形纸条 DEFG，其中 E，F 在 BC 上，点 G 在 AB 上，若 BF＝4.5cm，CE＝2cm，则纸 条 GD 的长为（ ） A．3 cm B．2 cm C． cm D． cm 9．已知 A（m，2020），B（m+n，2020）是抛物线 y＝﹣（x﹣h）2+2036 上两点，则正数 n ＝（ ） A．2 B．4 C．8 D．16 10．如图，点 A，B，C 均在坐标轴上，AO＝BO＝CO＝1，过 A，O，C 作 ⊙ D，E 是 ⊙ D 上 任意一点，连结 CE，BE，则 CE2+BE2 的最大值是（ ） 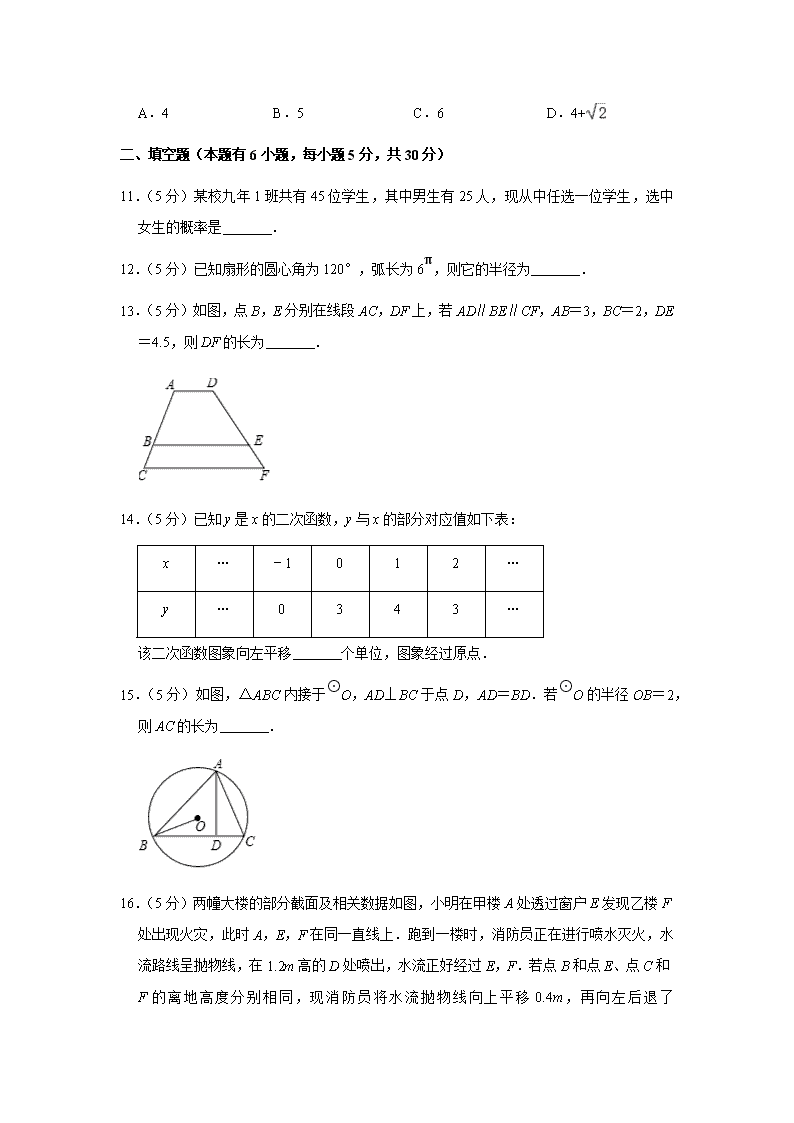A．4 B．5 C．6 D．4+ 二、填空题（本题有 6 小题，每小题 5 分，共 30 分） 11．（5 分）某校九年 1 班共有 45 位学生，其中男生有 25 人，现从中任选一位学生，选中 女生的概率是 ． 12．（5 分）已知扇形的圆心角为 120°，弧长为 6 π ，则它的半径为 ． 13．（5 分）如图，点 B，E 分别在线段 AC，DF 上，若 AD∥BE∥CF，AB＝3，BC＝2，DE ＝4.5，则 DF 的长为 ． 14．（5 分）已知 y 是 x 的二次函数，y 与 x 的部分对应值如下表： x … ﹣1 0 1 2 … y … 0 3 4 3 … 该二次函数图象向左平移 个单位，图象经过原点． 15．（5 分）如图，△ABC 内接于 ⊙ O，AD⊥BC 于点 D，AD＝BD．若 ⊙ O 的半径 OB＝2， 则 AC 的长为 ． 16．（5 分）两幢大楼的部分截面及相关数据如图，小明在甲楼 A 处透过窗户 E 发现乙楼 F 处出现火灾，此时 A，E，F 在同一直线上．跑到一楼时，消防员正在进行喷水灭火，水 流路线呈抛物线，在 1.2m 高的 D 处喷出，水流正好经过 E，F．若点 B 和点 E、点 C 和 F 的离地高度分别相同，现消防员将水流抛物线向上平移 0.4m，再向左后退了 m， 恰好把水喷到 F 处进行灭火． 三、解答题（本题有 8 小题，共 80 分，解答需写出必要的文字说明、演算步骤或证明过程） 17．（8 分）如图，在 6×6 的正方形网格中，网线的交点称为格点，点 A，B，C 都是格点．已 知每个小正方形的边长为 1． （1）画出△ABC 的外接圆 ⊙ O，并直接写出 ⊙ O 的半径是多少． （2）连结 AC，在网络中画出一个格点 P，使得△PAC 是直角三角形，且点 P 在 ⊙ O 上． 18．（8 分）已知点（0，3）在二次函数 y＝ax2+bx+c 的图象上，且当 x＝1 时，函数 y 有最 小值 2． （1）求这个二次函数的表达式． （2）如果两个不同的点 C（m，6），D（n，6）也在这个函数的图象上，求 m+n 的值． 19．（8 分）如图，△ABC 中，AB＝AC，以 AB 为直径作 ⊙ O，交 BC 于点 D，交 AC 于点 E． （1）求证： ． （2）若∠BAC＝50°，求 的度数． 20．（10 分）如图，将矩形 ABCD 沿 EF 折叠，使顶点 C 恰好落在 AB 边的 C1 处，点 D 落 在点 D1 处，C1D1 交线段 AE 于点 G． （1）求证：△BC1F∽△AGC1； （2）若 C1 是 AB 的中点，AB＝6，BC＝9，求 AG 的长． 21．（10 分）如图直角坐标系中，O 为坐标原点，抛物线 y＝﹣x2+6x+3 交 y 轴于点 A，过 A 作 AB∥x 轴，交抛物线于点 B，连结 OB．点 P 为抛物线上 AB 上方的一个点，连结 PA， 作 PQ⊥AB 垂足为 H，交 OB 于点 Q． （1）求 AB 的长； （2）当∠APQ＝∠B 时，求点 P 的坐标； （3）当△APH 面积是四边形 AOQH 面积的 2 倍时，求点 P 的坐标． 22．（10 分）如图，AB 是 ⊙ O 的直径，弦 CD⊥AB 于点 E，G 是 上一点，AG，DC 的延 长线交于点 F． （1）求证：∠FGC＝∠AGD． （2）当 DG 平分∠AGC，∠ADG＝45°，AF＝ ，求弦 DC 的长． 23．（12 分）自 2019 年 3 月开始，我国生猪、猪肉价格持续上涨，某大型菜场在销售过程 中发现，从 2019 年 10 月 1 日起到 11 月 9 日的 40 天内，猪肉的每千克售价与上市时间 的关系用图 1 的一条折线表示：猪肉的进价与上市时间的关系用图 2 的一段抛物线 y＝a （x﹣30）2+100 表示． （1）a＝ ； （2）求图 1 表示的售价 p 与时间 x 的函数关系式； （3）问从 10 月 1 日起到 11 月 9 日的 40 天内第几天每千克猪肉利润最低，最低利润为 多少？ 24．（14 分）如图 Rt△ABC 中，∠ABC＝90°，P 是斜边 AC 上一个动点，以 BP 为直径作 ⊙ O 交 BC 于点 D，与 AC 的另一个交点 E，连接 DE． （1）当 时， ① 若 ＝130°，求∠C 的度数； ② 求证 AB＝AP； （2）当 AB＝15，BC＝20 时 ① 是否存在点 P，使得△BDE 是等腰三角形，若存在，求出所有符合条件的 CP 的长； ② 以 D 为端点过 P 作射线 DH，作点 O 关于 DE 的对称点 Q 恰好落在∠CPH 内，则 CP 的取值范围为 ．（直接写出结果） 2020-2021 学年浙江省温州市南浦实验中学九年级（上）期末数 学试卷 参考答案与试题解析 一、选择题（本题有 10 小题，每小题 4 分，共 40 分.每小题只有一个选项是正确的，不选、 多选、错选均不给分） 1．若 ，则 的值等于（ ） A． B． C． D． 【分析】根据比例的性质即可得到结论． 【解答】解：∵ ， ∴设 b＝3k，a＝2k， ∴ ＝ ＝ ， 故选：B． 2． ⊙ O 的半径为 4cm，若点 P 到圆心的距离为 3cm，点 P 在（ ） A．圆内 B．圆上 C．圆外 D．无法确定 【分析】直接根据点与圆的位置关系进行判断． 【解答】解：∵点 P 到圆心的距离为 3cm， 而 ⊙ O 的半径为 4cm， ∴点 P 到圆心的距离小于圆的半径， ∴点 P 在圆内． 故选：A． 3．二次函数 y＝x2﹣1 的图象与 y 轴的交点坐标是（ ） A．（0，1） B．（1，0） C．（﹣1，0） D．（0，﹣1） 【分析】令 x＝0，求出 y 的值，即可解决问题； 【解答】解：对于二次函数 y＝x2﹣1，令 x＝0，得到 y＝﹣1， 所以二次函数与 y 轴的交点坐标为（0，﹣1）， 故选：D． 4．若一个圆内接正多边形的内角是 108°，则这个多边形是（ ） A．正五边形 B．正六边形 C．正八边形 D．正十边形 【分析】通过内角求出外角，利用多边形外角和 360 度，用 360°除以外角度数即可求出 这个正多边形的边数． 【解答】解：∵正多边形的每个内角都相等，且为 108°， ∴其一个外角度数为 180°﹣108°＝72°， 则这个正多边形的边数为 360°÷72°＝5， 故选：A． 5．一个不透明的盒子里有 n 个除颜色外其他完全相同的小球，其中有 9 个黄球．每次摸球 前先将盒子里的球摇匀，任意摸出一个球记下颜色后再放回盒子，通过大量重复摸球实 验后发现，摸到黄球的频率稳定在 30%，那么估计盒子中小球的个数 n 为（ ） A．20 B．24 C．28 D．30 【分析】根据利用频率估计概率得到摸到黄球的概率为 30%，然后根据概率公式计算 n 的值． 【解答】解：根据题意得 ＝30%，解得 n＝30， 所以这个不透明的盒子里大约有 30 个除颜色外其他完全相同的小球． 故选：D． 6．已知二次函数的图象（0≤x≤4）如图，关于该函数在所给自变量的取值范围内，下列说 法正确的是（ ） A．有最大值 2，有最小值﹣2.5 B．有最大值 2，有最小值 1.5 C．有最大值 1.5，有最小值﹣2.5 D．有最大值 2，无最小值 【分析】根据二次函数的图象，可知函数 y 的最大值和最小值． 【解答】解：观察图象可得，在 0≤x≤4 时，图象有最高点和最低点， ∴函数有最大值 2 和最小值﹣2.5， 故选：A． 7．如图，D 是等边△ABC 外接圆上的点，且∠DAC＝20°，则∠ACD 的度数为（ ） A．20° B．30° C．40° D．45° 【分析】根据圆内接四边形的性质得到∠D＝180°﹣∠B＝120°，根据三角形内角和定 理计算即可． 【解答】解：∵△ABC 是等边三角形， ∴∠B＝60°， ∵四边形 ABCD 是圆内接四边形， ∴∠D＝180°﹣∠B＝120°， ∴∠ACD＝180°﹣∠DAC﹣∠D＝40°， 故选：C． 8．如图，有一块直角三角形余料 ABC，∠BAC＝90°，D 是 AC 的中点，现从中切出一条 矩形纸条 DEFG，其中 E，F 在 BC 上，点 G 在 AB 上，若 BF＝4.5cm，CE＝2cm，则纸 条 GD 的长为（ ） A．3 cm B．2 cm C． cm D． cm 【分析】根据题意推知△AGD∽△ABC，由该相似三角形的对应边成比例求得 GD 的长 度即可． 【解答】解：依题意得：△AGD∽△ABC， ∴ ＝ ，即 ＝ ， 解得 GD＝ （cm）． 故选：C． 9．已知 A（m，2020），B（m+n，2020）是抛物线 y＝﹣（x﹣h）2+2036 上两点，则正数 n ＝（ ） A．2 B．4 C．8 D．16 【分析】由 A（m，2020），B（m+n，2020）是抛物线 y＝﹣（x﹣h）2+2036 上两点，可 得 A（h﹣4，2020），B（h+4，2020），即可得到 m＝h﹣4，m+n＝h+4，进而即可求得 n ＝8． 【解答】解：∵A（m，2020），B（m+n，2020）是抛物线 y＝﹣（x﹣h）2+2036 上两点， ∴2020＝﹣（x﹣h）2+2036， 解得 x1＝h﹣4，x2＝h+4， ∴A（h﹣4，2020），B（h+4，2020）， ∵m＝h﹣4，m+n＝h+4， ∴n＝8， 故选：C． 10．如图，点 A，B，C 均在坐标轴上，AO＝BO＝CO＝1，过 A，O，C 作 ⊙ D，E 是 ⊙ D 上 任意一点，连结 CE，BE，则 CE2+BE2 的最大值是（ ） A．4 B．5 C．6 D．4+ 【分析】连接 AC，DE，如图，利用圆周角定理可判定点 D 在 AC 上，易得 A（0，1）， B（﹣1，0），C（1，0），AC＝ ，D（ ， ），设 E（m，n），利用两点间的距离公 式得到则 EB2+EC2＝2（m2+n2）+2，由于 m2+n2 表示 E 点到原点的距离，则当 OE 为直 径时，E 点到原点的距离最大，由于 OD 为平分∠AOC，则 m＝n，利用点 E 在圆上得到 （m﹣ ）2+（n﹣ ）2＝（ ）2，则可计算出 m＝n＝1，从而得到 EB2+EC2 的最大 值． 【解答】解：连接 AC，DE，如图， ∵∠AOC＝90°， ∴AC 为 ⊙ D 的直径， ∴点 D 在 AC 上， ∵AO＝BO＝CO＝1， ∴A（0，1），B（﹣1，0），C（1，0），AC＝ ，D（ ， ）， 设 E（m，n）， ∵EB2+EC2＝（m﹣1）2+n2+（m+1）2+n2 ＝2（m2+n2）+2， 而 m2+n2 表示 E 点到原点的距离， ∴当 OE 为直径时，E 点到原点的距离最大， ∵OD 为平分∠AOC， ∴m＝n， ∵DE＝ AC＝ ， ∴（m﹣ ）2+（n﹣ ）2＝（ ）2， 即 m2+n2＝m+n ∴m＝n＝1， ∴此时 EB2+EC2＝2（m2+n2）+2＝2（1+1）+2＝6， 即 CE2+BE2 的最大值是 6． 故选：C． 二、填空题（本题有 6 小题，每小题 5 分，共 30 分） 11．（5 分）某校九年 1 班共有 45 位学生，其中男生有 25 人，现从中任选一位学生，选中 女生的概率是 ． 【分析】先求出女生的人数，再用女生人数除以总人数即可得出答案． 【解答】解：∵共有 45 位学生，其中男生有 25 人， ∴女生有 20 人， ∴选中女生的概率是 ＝ ； 故答案为： ． 12．（5 分）已知扇形的圆心角为 120°，弧长为 6 π ，则它的半径为 9 ． 【分析】根据弧长的公式 l＝ ，计算即可． 【解答】解：设扇形的半径为 R， 由题意得， ＝6 π ， 解得，R＝9， 故答案为：9． 13．（5 分）如图，点 B，E 分别在线段 AC，DF 上，若 AD∥BE∥CF，AB＝3，BC＝2，DE ＝4.5，则 DF 的长为 7.5 ． 【分析】根据平行线分线段成比例定理列出比例式，计算即可． 【解答】解：∵AD∥BE∥CF， ∴ ＝ ，即 ＝ ， 解得，EF＝3， ∴DF＝DE+EF＝7.5， 故答案为：7.5． 14．（5 分）已知 y 是 x 的二次函数，y 与 x 的部分对应值如下表： x … ﹣1 0 1 2 … y … 0 3 4 3 … 该二次函数图象向左平移 3 个单位，图象经过原点． 【分析】利用表格中的对称性得：抛物线与 x 轴另一个交点为（3，0），可得结论． 【解答】解：由表格得：二次函数的对称轴是直线 x＝ ＝1． ∵抛物线与 x 轴另一个交点为（﹣1，0）， ∴抛物线与 x 轴另一个交点为（3，0）， ∴该二次函数图象向左平移 3 个单位，图象经过原点；或该二次函数图象向右平移 1 个 单位，图象经过原点． 故答案为 3． 15．（5 分）如图，△ABC 内接于 ⊙ O，AD⊥BC 于点 D，AD＝BD．若 ⊙ O 的半径 OB＝2， 则 AC 的长为 2 ． 【分析】连接 OA、OC，根据等腰直角三角形的性质得到∠ABC＝45°，根据圆周角定 理求出∠AOC，根据勾股定理计算即可． 【解答】解：连接 OA、OC， ∵AD⊥BC，AD＝BD， ∴∠ABC＝45°， 由圆周角定理得，∠AOC＝2∠ABC＝90°， ∴AC＝ OA＝2 ， 故答案为：2 ． 16．（5 分）两幢大楼的部分截面及相关数据如图，小明在甲楼 A 处透过窗户 E 发现乙楼 F 处出现火灾，此时 A，E，F 在同一直线上．跑到一楼时，消防员正在进行喷水灭火，水 流路线呈抛物线，在 1.2m 高的 D 处喷出，水流正好经过 E，F．若点 B 和点 E、点 C 和 F 的离地高度分别相同，现消防员将水流抛物线向上平移 0.4m，再向左后退了 ﹣ 10 m，恰好把水喷到 F 处进行灭火． 【分析】由图形得出点 A（0，21.2）、D（0，1.2）、E（20，9.2）、点 F 的纵坐标为 6.2， 先利用待定系数法求得直线 AE 解析式，据此求得点 F 的坐标，再根据点 D、E、F 的坐 标求得抛物线的解析式为 y＝﹣ x2+ x+ ＝﹣ （x﹣15）2+ ，若设向左移动的 距离为 p，则移动后抛物线的解析式为 y＝﹣ （x+p﹣15）2+ + ，将点 F 坐标代入 求得 p 的值即可． 【解答】解：由图形可知，点 A（0，21.2）、D（0，1.2）、E（20，9.2）、点 F 的纵坐标 为 6.2 设 AE 所在直线解析式为 y＝mx+n， 则 ， 解得： ， ∴直线 AE 解析式为 y＝﹣0.6x+21.2， 当 y＝6.2 时，﹣0.6x+21.2＝6.2， 解得：x＝25， ∴点 F 坐标为（25，6.2）， 设抛物线的解析式为 y＝ax2+bx+c， 将点 D（0，1.2）、E（20，9.2）、F（25，6.2）代入，得： ， 解得： ， ∴抛物线的解析式为 y＝﹣ x2+ x+ ＝﹣ （x﹣15）2+ ， 设消防员向左移动的距离为 p（p＞0）， 则移动后抛物线的解析式为 y＝﹣ （x+p﹣15）2+ + ， 根据题意知，平移后抛物线过点 F（25，6.2），代入得： ﹣ （25+p﹣15）2+ + ＝6.2， 解得：p＝﹣ ﹣10（舍）或 p＝ ﹣10， 即消防员将水流抛物线向上平移 0.4m，再向左后退了（ ﹣10）m，恰好把水喷到 F 处进行灭火， 故答案为： ﹣10． 三、解答题（本题有 8 小题，共 80 分，解答需写出必要的文字说明、演算步骤或证明过程） 17．（8 分）如图，在 6×6 的正方形网格中，网线的交点称为格点，点 A，B，C 都是格点．已 知每个小正方形的边长为 1． （1）画出△ABC 的外接圆 ⊙ O，并直接写出 ⊙ O 的半径是多少． （2）连结 AC，在网络中画出一个格点 P，使得△PAC 是直角三角形，且点 P 在 ⊙ O 上． 【分析】（1）直接利用网格结合勾股定理得出答案； （2）字节利用圆周角定理得出 P 点位置． 【解答】解：（1）如图所示： ⊙ O 即为所求， ⊙ O 的半径是： ＝ ； （2）如图所示：直角三角形 PAC 即为所求． 18．（8 分）已知点（0，3）在二次函数 y＝ax2+bx+c 的图象上，且当 x＝1 时，函数 y 有 最小值 2． （1）求这个二次函数的表达式． （2）如果两个不同的点 C（m，6），D（n，6）也在这个函数的图象上，求 m+n 的值． 【分析】（1）由题意可得（1，2）是抛物线的顶点，且过（0，3），可利用顶点式求出关 系式； （2）根据点 C（m，6），D（n，6）坐标特点可知这两个点关于对称轴对称，可求出 m+n 的值． 【解答】解：（1）∵二次函数 y＝ax2+bx+c 当 x＝1 时，函数 y 有最小值 2， ∴点（1，2）为抛物线的顶点， 于是可设抛物线的关系式为 y＝a（x﹣1）2+2，把（0，3）代入得， a+2＝3， ∴a＝1， ∴抛物线的关系式为 y＝（x﹣1）2+2， 即 y＝x2﹣2x+3； （2）点 C（m，6），D（n，6）都在抛物线上， 因此点 C、D 关于直线 x＝1 对称， ∴ ＝1， ∴m+n＝2． 19．（8 分）如图，△ABC 中，AB＝AC，以 AB 为直径作 ⊙ O，交 BC 于点 D，交 AC 于点 E． （1）求证： ． （2）若∠BAC＝50°，求 的度数． 【分析】（1）连接 AD，先由圆周角定理得∠ADB＝90°，则 AD⊥BC，再由等腰三角形 的性质得∠BAD＝∠CAD，即可得出结论； （2）连接 OE，先由等腰三角形的性质得∠OEA＝∠BAC＝50°，再由三角形内角和定 理求出∠AOE＝80°，即可得出结论． 【解答】（1）证明：连接 AD，如图 1 所示： ∵AB 是 ⊙ O 的直径， ∴∠ADB＝90°， ∴AD⊥BC， ∵AB＝AC， ∴∠BAD＝∠CAD， ∴ ． （2）解：连接 OE，如图 2 所示： ∵AB 是 ⊙ O 的直径， ∴OA 是半径， ∴OA＝OE， ∴∠OEA＝∠BAC＝50°， ∴∠AOE＝180°﹣50°﹣50°＝80°， ∴ 的度数为 80°． 20．（10 分）如图，将矩形 ABCD 沿 EF 折叠，使顶点 C 恰好落在 AB 边的 C1 处，点 D 落 在点 D1 处，C1D1 交线段 AE 于点 G． （1）求证：△BC1F∽△AGC1； （2）若 C1 是 AB 的中点，AB＝6，BC＝9，求 AG 的长． 【分析】（1）根据题意和图形可以找出△BC1F∽△AGC1 的条件，从而可以解答本题； （2）根据勾股定理和（1）中的结论可以求得 AG 的长． 【解答】证明：（1）由题意可知∠A＝∠B＝∠GC1F＝90°， ∴∠BFC1+∠BC1F＝90°，∠AC1G+∠BC1F＝90°， ∴∠BFC1＝∠AC1G， ∴△BC1F∽△AGC1． （2）∵C1 是 AB 的中点，AB＝6， ∴AC1＝BC1＝3． ∵∠B＝90°， ∴BF2+32＝（9﹣BF）2， ∴BF＝4， 由（1）得△AGC1∽△BC1F， ∴ ， ∴ ， 解得，AG＝ ． 21．（10 分）如图直角坐标系中，O 为坐标原点，抛物线 y＝﹣x2+6x+3 交 y 轴于点 A，过 A 作 AB∥x 轴，交抛物线于点 B，连结 OB．点 P 为抛物线上 AB 上方的一个点，连结 PA， 作 PQ⊥AB 垂足为 H，交 OB 于点 Q． （1）求 AB 的长； （2）当∠APQ＝∠B 时，求点 P 的坐标； （3）当△APH 面积是四边形 AOQH 面积的 2 倍时，求点 P 的坐标． 【分析】（1）对于 y＝﹣x2+6x+3，令 x＝0，则 y＝3，故点 A（0，3），令 y＝﹣x2+6x+3 ＝3，解得 x＝0 或 6，故点 B（6，3），即可求解； （2）证明△ABO～△HPA，则 ，即可求解； （3）当△APH 的面积是四边形 AOQH 的面积的 2 倍时，则 2（AO+HQ）＝PH，即可求 解． 【解答】解：（1）对于 y＝﹣x2+6x+3，令 x＝0，则 y＝3，故点 A（0，3）， 令 y＝﹣x2+6x+3＝3，解得 x＝0 或 6，故点 B（6，3）， 故 AB＝6； （2）设 P（m，﹣m2+6m+3）， ∵∠P＝∠B，∠AHP＝∠OAB＝90°， ∴△ABO～△HPA，故 ， ∴ ＝ ， 解得 m＝4． ∴P（4，11）； （3）当△APH 的面积是四边形 AOQH 的面积的 2 倍时， 则 2（AO+HQ）＝PH， ∴2（3+ ）＝﹣m2+6m， 解得：m1＝4，m2＝3， ∴P（4，11）或 P（3，12）． 22．（10 分）如图，AB 是 ⊙ O 的直径，弦 CD⊥AB 于点 E，G 是 上一点，AG，DC 的延 长线交于点 F． （1）求证：∠FGC＝∠AGD． （2）当 DG 平分∠AGC，∠ADG＝45°，AF＝ ，求弦 DC 的长． 【分析】（1）如图 1，利用垂径定理得到 ＝ ，根据等腰三角形的性质得∠ADC＝∠ ACD，根据圆周角定理的推论得到∠AGD＝∠ACD＝∠ADC，再利用圆内接四边形的性 质得到∠FGC＝∠ADC，从而得到结论； （2）连接 BG，AC，如图 2，根据垂径定理得到 DE＝CE，先证明△AEF 是等腰直角三 角形，可得 AE 的长，最后利用勾股定理可得 DE 的长，从而得 CD 的长． 【解答】（1）证明：如图 1，连接 AC， ∵AB 是 ⊙ O 的直径，弦 CD⊥AB， ∴ ＝ ， ∴AD＝AC， ∴∠ADC＝∠ACD， ∵ADCG 在 ⊙ O 上， ∴∠CGF＝∠ADC， ∵∠AGD＝∠ACD， ∴∠FGC＝∠AGD； （2）解：如图 2，连接 BG，AC， ∵AB 是 ⊙ O 的直径，弦 CD⊥AB， ∴DE＝CE， ∵DG 平分∠AGC， ∴∠AGD＝∠CGD， ∵∠FGC＝∠AGD， ∴∠AGD＝∠CGD＝∠FGC， ∵∠AGD+∠CGD+∠FGC＝180°， ∴∠CGF＝∠AGD＝60°， ∴∠ADC＝∠ACD＝60°， ∴△ADC 是等边三角形， ∵AB⊥CD， ∴∠CAE＝∠DAE＝30°， ∵∠ADG＝45°， ∴∠CDG＝∠CAG＝60°﹣45°＝15°， ∴∠EAF＝30°+15°＝45°， Rt△AEF 中，AE＝EF， ∵AF＝ ， ∴AE＝EF＝ ， Rt△ADE 中，∠DAE＝30°， ∴DE＝1， ∴DC＝2DE＝2． 23．（12 分）自 2019 年 3 月开始，我国生猪、猪肉价格持续上涨，某大型菜场在销售过程 中发现，从 2019 年 10 月 1 日起到 11 月 9 日的 40 天内，猪肉的每千克售价与上市时间 的关系用图 1 的一条折线表示：猪肉的进价与上市时间的关系用图 2 的一段抛物线 y＝a （x﹣30）2+100 表示． （1）a＝ ﹣ ； （2）求图 1 表示的售价 p 与时间 x 的函数关系式； （3）问从 10 月 1 日起到 11 月 9 日的 40 天内第几天每千克猪肉利润最低，最低利润为 多少？ 【分析】（1）把（10，60）代入 y＝a（x﹣30）2+100 可得结论． （2）分两种情形，分别利用待定系数法解决问题即可． （3）分两种情形，分别求解即可． 【解答】解：（1）把（10，60）代入 y＝a（x﹣30）2+100，得到 a＝﹣ ， 故答案为﹣ ． （2）当 0≤x＜30 时，设 P＝kx+b， 把（0，60），（10，80）代入得到 ， 解得 ， ∴P＝2x+60． 当 30≤x≤40 时，设 P＝k′x+b′， 把（30，120），（40，100）代入得到 ， 解得 ， ∴P＝﹣2x+180． 综上所述，P＝ ． （3）设利润为 w． 当 0≤x＜30 时，w＝2x+60﹣（﹣ x2+6x+10）＝ x2﹣4x+50＝ （x﹣20）2+10， ∴当 x＝20 时，w 有最小值，最小值为 10（元/千克）． 当 30≤x≤40 时， w＝﹣2x+180﹣（﹣ x2+6x+10）＝ x2﹣8x+170＝ （x﹣40）2+10， ∴当 x＝40 时，最小利润 w＝10（元/千克）， 综上所述，当 20 天或 40 天，最小利润为 10 元/千克． 24．（14 分）如图 Rt△ABC 中，∠ABC＝90°，P 是斜边 AC 上一个动点，以 BP 为直径作 ⊙ O 交 BC 于点 D，与 AC 的另一个交点 E，连接 DE． （1）当 时， ① 若 ＝130°，求∠C 的度数； ② 求证 AB＝AP； （2）当 AB＝15，BC＝20 时 ① 是否存在点 P，使得△BDE 是等腰三角形，若存在，求出所有符合条件的 CP 的长； ② 以 D 为端点过 P 作射线 DH，作点 O 关于 DE 的对称点 Q 恰好落在∠CPH 内，则 CP 的取值范围为 7＜CP＜12.5 ．（直接写出结果） 【分析】（1） ① 连接 BE，由圆周角定理得出∠BEC＝90°，求出 ＝50°， ＝100°， 则∠CBE＝50°，即可得出结果； ② 由 ＝ ，得出∠CBP＝∠EBP，易证∠C＝∠ABE，由∠APB＝∠CBP+∠C，∠ABP ＝∠EBP+∠ABE，得出∠APB＝∠ABP，即可得出结论； （2） ① 由勾股定理得 AC＝ ＝25，由面积公式得出 AB•BC＝ AC•BE，求 出 BE＝12，连接 DP，则 PD∥AB，得出△DCP∽△BCA，求出 CP＝ ＝ CD， △BDE 是等腰三角形，分三种情况讨论，当 BD＝BE 时，BD＝BE＝12，CD＝BC﹣BD ＝8，CP＝ CD＝10；当 BD＝ED 时，可知点 D 是 Rt△CBE 斜边的中线，得出 CD＝ BC ＝10，CP＝ CD＝ ；当 DE＝BE 时，作 EH⊥BC，则 H 是 BD 中点，EH∥AB，求 出 AE＝ ＝9，CE＝AC﹣AE＝16，CH＝20﹣BH，由 EH∥AB，得出 ＝ ， 求出 BH＝ ，BD＝2BH＝ ，CD＝BC﹣BD＝ ，则 CP＝ CD＝7； ② 当点 Q 落在∠CPH 的边 PH 上时，CP 最小，连接 OD、OQ、OE、QE、BE，证明四 边形 ODQE 是菱形，求出 PC＝AC﹣PE﹣AE＝7；当点 Q 落在∠CPH 的边 PC 上时，CP 最大，连接 OD、OQ、OE、QD，同理得四边形 ODQE 是菱形，连接 DF，求出 PC＝ AC ＝12.5，即可得出答案． 【解答】（1） ① 解：连接 BE，如图 1 所示： ∵BP 是直径， ∴∠BEC＝90°， ∵ ＝130°， ∴ ＝50°， ∵ ＝ ， ∴ ＝100°， ∴∠CBE＝50°， ∴∠C＝40°； ② 证明：∵ ＝ ， ∴∠CBP＝∠EBP， ∵∠ABE+∠A＝90°，∠C+∠A＝90°， ∴∠C＝∠ABE，∵∠APB＝∠CBP+∠C，∠ABP＝∠EBP+∠ABE， ∴∠APB＝∠ABP， ∴AP＝AB； （2）解： ① 由 AB＝15，BC＝20， 由勾股定理得：AC＝ ＝ ＝25， ∵ AB•BC＝ AC•BE， 即 ×15×20＝ ×25×BE ∴BE＝12， 连接 DP，如图 1﹣1 所示： ∵BP 是直径， ∴∠PDB＝90°， ∵∠ABC＝90°， ∴PD∥AB， ∴△DCP∽△BCA， ∴ ＝ ， ∴CP＝ ＝ ＝ CD， △BDE 是等腰三角形，分三种情况： 当 BD＝BE 时，BD＝BE＝12， ∴CD＝BC﹣BD＝20﹣12＝8， ∴CP＝ CD＝ ×8＝10； 当 BD＝ED 时，可知点 D 是 Rt△CBE 斜边的中线， ∴CD＝ BC＝10， ∴CP＝ CD＝ ×10＝ ； 当 DE＝BE 时，作 EH⊥BC，则 H 是 BD 中点，EH∥AB，如图 1﹣2 所示： AE＝ ＝ ＝9， ∴CE＝AC﹣AE＝25﹣9＝16，CH＝BC﹣BH＝20﹣BH， ∵EH∥AB， ∴ ＝ ， 即 ＝ ， 解得：BH＝ ， ∴BD＝2BH＝ ， ∴CD＝BC﹣BD＝20﹣ ＝ ， ∴CP＝ CD＝ × ＝7； 综上所述，△BDE 是等腰三角形，符合条件的 CP 的长为 10 或 或 7； ② 当点 Q 落在∠CPH 的边 PH 上时，CP 最小，如图 2 所示： 连接 OD、OQ、OE、QE、BE， 由对称的性质得：DE 垂直平分 OQ， ∴OD＝QD，OE＝QE， ∵OD＝OE， ∴OD＝OE＝QD＝QE， ∴四边形 ODQE 是菱形， ∴PQ∥OE， ∵PB 为直径， ∴∠PDB＝90°， ∴PD⊥BC， ∵∠ABC＝90°， ∴AB⊥BC， ∴PD∥AB， ∴DE∥AB， ∵OB＝OP， ∴OE 为△ABP 中位线， ∴PE＝AE＝9， ∴PC＝AC﹣PE﹣AE＝25﹣9﹣9＝7； 当点 Q 落在∠CPH 的边 PC 上时，CP 最大，如图 3 所示： 连接 OD、OQ、OE、QD， 同理得：四边形 ODQE 是菱形， ∴OD∥QE， 连接 DF， ∵∠DBA＝90°， ∴DF 是直径， ∴D、O、F 三点共线， ∴DF∥AQ， ∴∠OFB＝∠A， ∵OB＝OF， ∴∠OFB＝∠OBF＝∠A， ∴PA＝PB， ∵∠OBF+∠CBP＝∠A+∠C＝90°， ∴∠CBP＝∠C， ∴PB＝PC＝PA， ∴PC＝ AC＝12.5， ∴7＜CP＜12.5， 故答案为：7＜CP＜12.5．