人教版七年级上册期末复习高频考点专题练习一遍过：一元一次方程实际应用（二） 10页

人教版七年级上册期末复习高频考点专题练习一遍过： 一元一次方程实际应用（二） 1．据北京市交通委介绍，兴延高速公路将服务于 2019 年延庆世园会及 2022 年冬奥会．兴 延高速南起西北六环双横立交，北至延庆京藏高速营城子立交收费站以北，昌平境内约 31 千米，延庆境内约 11 千米，全程的总造价约为 159 亿元；由于延庆段道路多穿过山 区，造价比昌平段每千米的平均造价多 3 亿元，求延庆段和昌平段的高速公路每千米的 平均造价各是多少亿元？ 2．已知 M，N 两点在数轴上所表示的数分别为 m，n 且满足|m﹣12|+（n+3）2＝0． （1）则 m＝ ，n＝ ； （2）若点 P 从 N 点出发，以每秒 1 个单位长度的速度向右运动，同时点 Q 从 M 点出发， 以每秒 1 个单位长度的速度向左运动，经过多长时间后 P，Q 两点相距 7 个单位长度？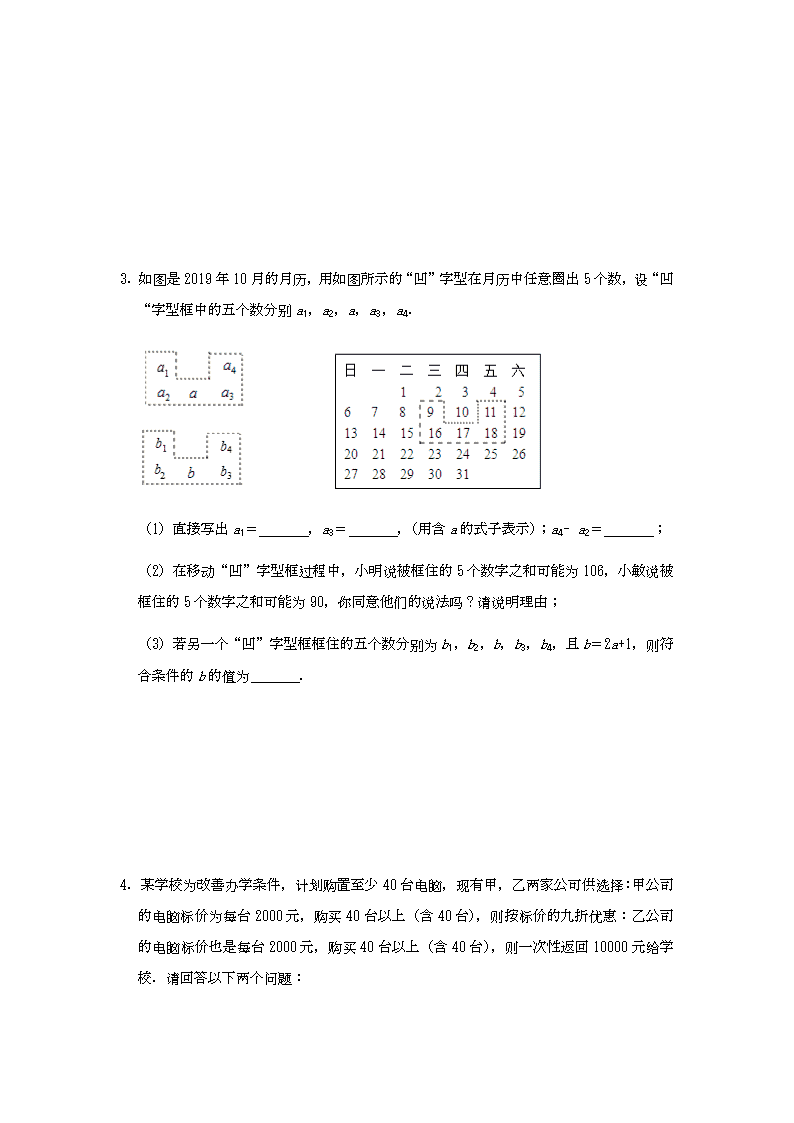 （3）若 A，B 为线段 MN 上的两点，且 NA＝AB＝BM，点 P 从点 N 出发，以每秒 2 个 单位长度的速度向左运动，点 Q 从 M 点出发，以每秒 4 个单位长度的速度向右运动， 点 R 从 B 点出发，以每秒 3 个单位长度的速度向右运动，P，Q，R 同时出发，是否存在 常数 k，使得 PQ﹣kAR 的值与它们的运动时间无关，为定值．若存在，请求出 k 和这个 定值；若不存在，请说明理由． 3．如图是 2019 年 10 月的月历，用如图所示的“凹”字型在月历中任意圈出 5 个数，设“凹 “字型框中的五个数分别 a1，a2，a，a3，a4． （1）直接写出 a1＝ ，a3＝ ，（用含 a 的式子表示）；a4﹣a2＝ ； （2）在移动“凹”字型框过程中，小明说被框住的 5 个数字之和可能为 106，小敏说被 框住的 5 个数字之和可能为 90，你同意他们的说法吗？请说明理由； （3）若另一个“凹”字型框框住的五个数分别为 b1，b2，b，b3，b4，且 b＝2a+1， 则符合条件的 b 的值为 ． 4．某学校为改善办学条件，计划购置至少 40 台电脑，现有甲，乙两家公可供选择：甲公 司的电脑标价为每台 2000 元，购买 40 台以上（含 40 台），则按标价的九折优惠：乙公 司的电脑标价也是每台 2000 元，购买 40 台以上（含 40 台），则一次性返回 10000 元给 学校．请回答以下两个问题： （1）设学校购买 x 台电脑（x≥40），请你用 x 分别表示出到甲、乙两公司购买电脑所需 的金额； （2）请问购买多少台电脑时，到甲、乙两公司购买电脑所需的金额一样？并说明理由． 5．列方程解应用题： 现有校舍面积 20000 平方米，为改善办学条件，计划拆除部分旧校舍，建造新校舍，使 新造校舍的面积是拆除旧校舍面积的 3 倍还多 1000 平方米．这样，计划完成后的校舍 总面积可比现有校舍面积增加 20%． （1）改造多少平方米旧校舍； （2）已知拆除旧校舍每平方米费用 80 元，建造新校舍每平方米需费用 700 元，问完成 该计划需多少费用． 6．阅读理解： 【探究与发现】 如图 1，在数轴上点 E 表示的数是 8，点 F 表示的数是 4，求线段 EF 的中点 M 所示的数 对于求中点表示数的问题，只要用点 E 所表示的数﹣8，加上点 F 所表示的数 4，得到的 结果再除以 2，就可以得到中点 M 所表示的数：即 M 点表示的数为： ． 【理解与应用】 把一条数轴在数 m 处对折，使表示﹣20 和 2020 两数的点恰好互相重合，则 m＝ ． 【拓展与延伸】 如图 2，已知数轴上有 A、B、C 三点，点 A 表示的数是﹣6，点 B 表示的数是 8．AC＝ 18． （1）若点 A 以每秒 3 个单位的速度向右运动，点 C 同时以每秒 1 个单位的速度向左运 动设运动时间为 t 秒． ①点 A 运动 t 秒后，它在数轴上表示的数表示为 （用含 t 的代数式表示） ②当点 B 为线段 AC 的中点时，求 t 的值． （2）若（1）中点 A、点 C 的运动速度、运动方向不变，点 P 从原点以每秒 2 个单位的 速度向右运动，假设 A、C、P 三点同时运动，求多长时间点 P 到点 A、C 的距离相等？ 7．为了庆祝伟大祖国成立七十周年，某班级把一批爱国主义图书分给学生阅读，如果每人 分 3 本，则剩余 20 本；如果每人分 4 本，还缺 25 本．该班有多少名学生？ 8．甲、乙两个仓库共有粮食 60t．甲仓库运进粮食 14t、乙仓库运出粮食 10t 后，两个仓库 的粮食数量相等．两个仓库原来各有粮食多少？ 9．方程应用题 （1）某车间有 55 名工人，每人每天可以生产 1200 个螺钉或 2000 个螺母．一个螺钉需 要配 2 个螺母，为使每天生产的螺钉和螺母刚好配套，应安排生产螺钉和螺母的工人各 多少名？ （2）某校七年级社会实践小组去商场调查商品销售情况，了解该商场以每件 80 元的价 格购进了某品牌衬衫 500 件，并以每件 120 元的价格销售了 400 件，商场准备采取促销 措施，将剩下的衬衫降价销售．请你帮商场计算一下，每件衬衫降价多少元时，销售完 这批衬衫正好达到盈利 45%的预期目标？ 10．【材料阅读】 角是一种基本的几何图形，如图 1 角可以看作由一条射线绕着它的端点旋转而形成的图 形，钟面上的时针与分针给我们以角的形象．如果把图 2 作为钟表的起始状态，对于一 个任意时刻时针与分针的夹角度数可以用下面的方法确定． 因为时针绕钟面转一圈（360°）需要 12 小时，所以时针每小时转过 30°． 如图 3 中 05：00 时针就转过 30×5＝150°． 因为分针绕钟面转一圈（360°）需要 60 分钟，所以分针每分钟转过 6°． 如图 4 中 00：28 分针就转过 6×28＝168°． 再如图 5 中 6：40 时针转过的度数为 30×（6+ ）＝200°，分针转过的度数记为 6 ×40＝240°，此时，分针转过的度数大于时针转过的度数，所以 6：40 时针与分针的 夹角为 240°﹣200°＝40°． 【知识应用】 请使用上述方法，求出 7：20 时针与分针的夹角． 【拓广探索】 张老师某周六上午 7 点多去菜市场买菜，走时发现家中钟表时针与分针的夹角是直角， 买菜回到家发现钟表时针与分针的夹角还是直角，可以确定的是张老师家的钟表没有故 障，走时正常，且回家时间还没到上午 8 点，请利用上述材料所得建立数学模型列方程， 求出张老师约 7 点多少分出门买菜？约 7 点多少分回到家？（结果用四舍五入法精确到 分．） 参考答案 1．解：设昌平段的高速公路每千米的平均造价为 x 亿元，则延庆段的高速公路每千米的平 均造价为（x+3）亿元． 由题意列方程为： 31x+11（x+3）＝159． 解此方程得：x＝3． ∴x+3＝6． 答：昌平段和延庆段的高速公路每千米的平均造价分别为 3 亿元和 6 亿元． 2．解：（1）∵|m﹣12|+（n+3）2＝0， ∴m﹣12＝0，n+3＝0， ∴m＝12，n＝﹣3． 故答案为：12；﹣3． （2）当运动时间为 t 秒时，点 P 对应的数是﹣3+t，点 Q 对应的数是 12﹣t， 依题意，得：|﹣3+t﹣（12﹣t）|＝7， 即 2t﹣15＝7 或 2t﹣15＝﹣7， 解得：t＝11 或 t＝4． 答：经过 4 秒或 11 秒后 P，Q 两点相距 7 个单位长度． （3）∵A，B 为线段 MN 上的两点，且 NA＝AB＝BM， ∴点 A 对应的数是﹣3+5＝2，点 B 对应的数是 12﹣5＝7． 当运动时间为 t 秒时，点 P 对应的数是﹣3﹣2t，点 Q 对应的数是 12+4t，点 R 对应的数 是 7+3t， ∴PQ＝|﹣3﹣2t﹣（12+4t）|＝15+6t，AR＝|2﹣（7+3t）|＝5+3t， ∴PQ﹣kAR＝15+6t﹣k（5+3t）＝15﹣5k+（6﹣3k）t， ∴当 k＝2 时，PQ﹣kAR 与它们的运动时间无关，为定值，该定值为 5． 3．解：（1）∵a1＝a﹣8，a2＝a﹣1，a3＝a+1，a4＝a﹣6， ∴a4﹣a2＝a﹣6﹣（a﹣1）＝﹣5． 故答案为：a﹣8；a+1；﹣5． （2）小明：（a﹣8）+（a﹣1）+a+（a+1）+（a﹣6）＝5a﹣14＝106， 解得：a＝24； 小敏：（a﹣8）+（a﹣1）+a+（a+1）+（a﹣6）＝5a﹣14＝90， 解得：a＝20.8（不符合题意，舍去）． ∴小明的说法对，小敏的说法不对． （3）a 的值可以为：9，10，11，14，15，16，17，18，21，22，23，24，25，28， 29，30， ∴2a+1 的值可以为：19，21，23，29，31，33，35，37，43，45，47，49，51，57， 59，61． ∵b 的值可以为：9，10，11，14，15，16，17，18，21，22，23，24，25，28，29， 30，且 b＝2a+1， ∴b 的值可以为：21，23，29． 故答案为：21，23 或 29． 4．解：（1）根据题意得：甲公司购买电脑所需的金额为：0.9×2000x＝1800x， 乙公司购买电脑所需的金额为：2000x﹣10000； （2）根据题意得：0.9×2000x＝2000x﹣10000； 解得 x＝50， ∴当购买 50 台时，甲、乙两公司购买电脑所需的金额一样； 5．解：（1）设需要拆除的旧校舍的面积是 x 平方米，则新造校舍的面积是（3x+1000）平 方米， 依题意，得：20000﹣x+3x+1000＝20000（1+20%）， 解得：x＝1500． 答：改造 1500 平方米旧校舍． （2）80×1500+700×（1500×3+1000）＝3970000（元）． 答：完成该计划需 3970000 元． 6．解：m＝ ＝1000； 故答案为：1000； （1）①点 A 向右移动的距离为 3t，因此点 A 从数轴上表示﹣6 的点向右移动 3t 的单位 后，所表示的数为 3t﹣6， 故答案为：3t﹣6， ②当点 B 为线段 AC 的中点时， Ⅰ）当移动后点 C 在点 B 的右侧时，此时 t＜4，如图 1， 由 BA＝BC 得，8﹣（3t﹣6）＝（12﹣t）﹣8， 解得，t＝5＞4（舍去） Ⅱ）当移动后点 C 在点 B 的左侧时，此时 t＞4，如图 2， 由 BA＝BC 得，（3t﹣6）﹣8＝8﹣（12﹣t）， 解得，t＝5， 答：当点 B 为线段 AC 的中点时，t 的值为 5 秒． （2）根据运动的方向、距离、速度可求出， 点 P、C 相遇时间为 12÷（2+1）＝4 秒， 点 A、C 相遇时间为 18÷（3+1）＝ 秒， 点 A 追上点 P 的时间为 6÷（3﹣2）＝6 秒， 当点 P 到点 A、C 的距离相等时， ①如图 2﹣3 所示，此时 t＜4， 由 PA＝PC 得，2t﹣（3t﹣6）＝（12﹣t）﹣2t， 解得，t＝3； ②当 A、C 相遇时符合题意，此时，t＝ ， ③当点 A 在点 P 的右侧，点 C 在点 P 的左侧时，此时 t＞6， ∵点 A 追上点 P 时用时 6 秒，之后 PA 距离每秒增加 1 个单位长度，而 PC 每秒增加 4 个单位长度， ∴不存在点 P 到点 A、C 的距离相等的情况， 因此：当点 P 到点 A、C 的距离相等时，t＝3 或 t＝ ． 7．解：设该班共有 x 名学生，则 3x+20＝4x﹣25 解得 x＝45 答：该班共有 45 名学生． 8．解：设甲仓库原来有粮食 xt，则乙仓库原来有粮食（60﹣x）t． 根据题意，得 x+14＝（60﹣x）﹣10， 解这个方程，得 x＝18． 则 60﹣x＝60﹣18＝42． 答：甲仓库原来有粮食 18t，乙仓库原来有粮食 42t． 9．解：（1）设应安排 x 名工人生产螺钉，（55﹣x）名工人生产螺母 根据题意，得 2000（55﹣x）＝2×1200x， 解得，x＝25， 55﹣x＝30， 答：应安排生产螺钉 25 名工人，生产螺母 30 名工人． （2）设每件衬衫降价 x 元，根据题意，得 120×400+（120﹣x）×100＝80×500×（1+45%）， 解得，x＝20， 答：每件衬衫降价 20 元时，销售完这批衬衫正好达到盈利 45%的预期目标 10．解：【知识应用】 ∵7：20 时针转过的度数为：30×（7+ ）＝220°，分针转过的度数为：6×20＝120°， ∴7：20 时针与分针的夹角为 220°﹣120°＝100°； 【拓广探索】 设七点后，经过 x 分钟，第一次时针与分针的夹角是直角， 根据题意可得：7×30+ x﹣6x＝90 解得：x≈22， 答：张老师约 7 点 22 分出门买菜， 设七点后，经过 y 分钟，第二次时针与分针的夹角是直角， 根据题意可得：6y﹣（7×30+ y）＝90 解得：y≈55 答：约 7 点 55 分回到家．