孝感市2020年中考数学试题及答案 30页

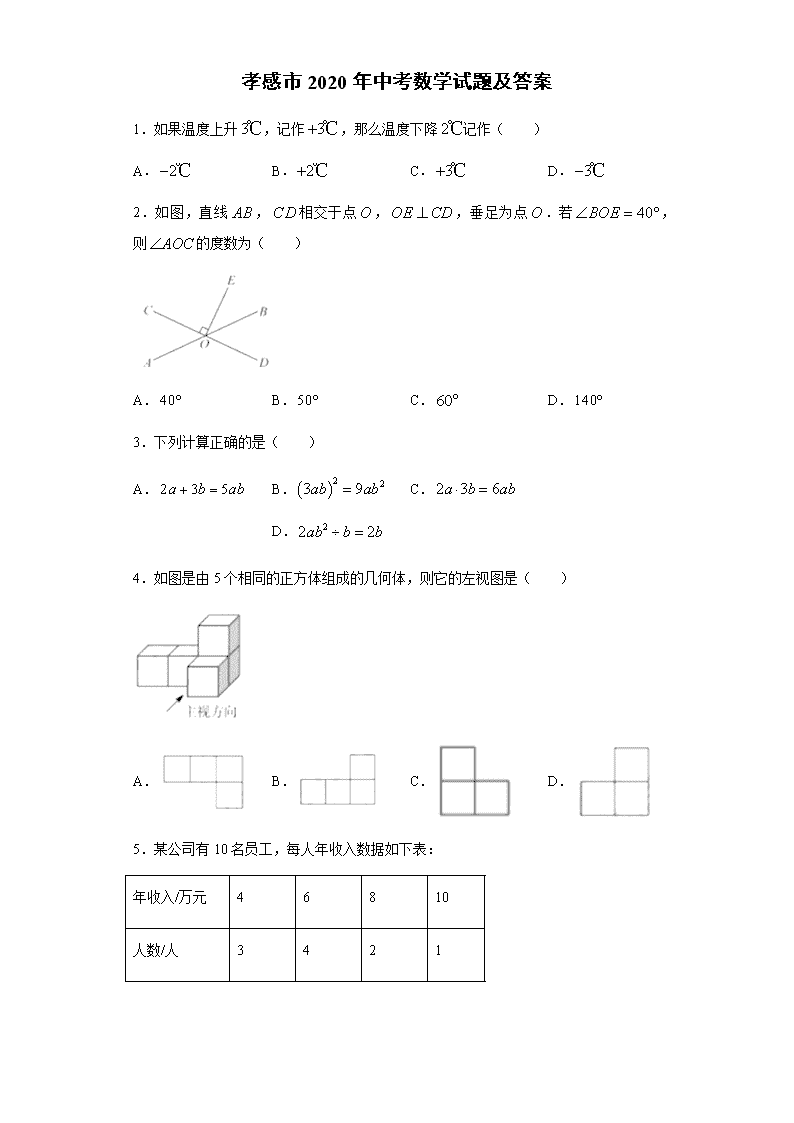
孝感市 2020 年中考数学试题及答案 1．如果温度上升3℃，记作 3 ℃，那么温度下降 2℃记作（ ） A． 2 ℃ B． 2 ℃ C． 3 ℃ D． 3 ℃ 2．如图，直线 AB ， CD 相交于点O ，OE CD ，垂足为点O ．若 40BOE   ， 则 AOC 的度数为（ ） A． 40 B．50 C． 60 D．140 3．下列计算正确的是（ ） A． 2 3 5a b ab  B． 2 23 9ab ab C． 2 3 6a b ab  D． 22 2ab b b  4．如图是由 5 个相同的正方体组成的几何体，则它的左视图是（ ） A． B． C． D． 5．某公司有 10 名员工，每人年收入数据如下表： 年收入/万元 4 6 8 10 人数/人 3 4 2 1 则他们年收入数据的众数与中位数分别为（ ） A．4，6 B．6，6 C．4，5 D．6，5 6．已知 5 1x   ， 5 1y   ，那么代数式   3 2x xy x x y   的值是（ ） A．2 B． 5 C．4 D． 2 5 7．已知蓄电池的电压为定值，使用蓄电池时，电流 I （单位： A ）与电阻 R （单位：  ）是反比例函数关系，它的图象如图所示．则这个反比例函数的解析式为（ ） A． 24I R  B． 36I R  C． 48I R  D． 64I R  8．将抛物线 2 1 : 2 3C y x x   向左平移 1 个单位长度，得到抛物线 2C ，抛物线 2C 与 抛物线 3C 关于 x 轴对称，则抛物线 3C 的解析式为（ ） A． 2 2y x   B． 2 2y x   C． 2 2y x  D． 2 2y x  9．如图，在四边形 ABCD 中， AD BC∥ ， 90D   ， 4AB  ， 6BC  ， 30BAD   ．动点 P 沿路径 A B C D   从点 A 出发，以每秒 1 个单位长度的速 度向点 D 运动．过点 P 作 PH AD ，垂足为 H ．设点 P 运动的时间为 x（单位：s ）， APHV 的面积为 y ，则 y 关于 x 的函数图象大致是（ ） A． B． C． D． 10．如图，点 E 在正方形 ABCD 的边 CD 上，将 ADE 绕点 A 顺时针旋转90 到 ABF 的位置，连接 EF ，过点 A 作 EF 的垂线，垂足为点 H ，与 BC 交于点G ．若 3BG  ， 2CG  ，则CE 的长为（ ） A． 5 4 B．15 4 C．4 D． 9 2 11．原子钟是北斗导航卫星的“心脏”，北斗卫星上的原子钟的精度可以达到 100 万年 以上误差不超过 1 秒．数据 100 万用科学记数法表示为______． 12．有一列数，按一定的规律排列成 1 3 ， 1 ，3， 9 ，27，－81，…．若其中某三个 相邻数的和是 567 ，则这三个数中第一个数是______． 13．某型号飞机的机翼形状如图所示，根据图中数据计算 AB 的长为______ m ．（结果 保留根号） 14．在线上教学期间，某校落实市教育局要求，督促学生每天做眼保健操．为了解落实 情况，学校随机抽取了部分学生进行调查，调查结果分为四类（A 类：总时长 5 分钟； B 类：5 分钟 总时长 10 分钟；C 类：10 分钟 总时长 15 分钟；D 类：总时长 15 分钟），将调查所得数据整理并绘制成如下两幅不完整的统计图． 该校共有 1200 名学生，请根据以上统计分析，估计该校每天做眼保健操总时长超过 5 分钟且不超过 10 分钟的学生约有______人． 15．如图 1，四个全等的直角三角形围成一个大正方形，中间是个小正方形，这个图形 是我国汉代赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”．在此图形中 连接四条线段得到如图 2 的图案，记阴影部分的面积为 1S ，空白部分的面积为 2S ，大 正方形的边长为 m ，小正方形的边长为 n ，若 1 2S S= ，则 n m 的值为______． 16．如图，已知菱形 ABCD 的对角线相交于坐标原点O ，四个顶点分别在双曲线 4y x  和  0ky kx   上， 2 3 AC BD  ．平行于 x 轴的直线与两双曲线分别交于点 E ， F ，连 接OE ，OF ，则 OEF 的面积为______． 17．计算： 0 3 18 3 1 2sin 60 4           18．如图，在 ABCD 中，点 E 在 AB 的延长线上，点 F 在CD 的延长线上，满足 BE DF ．连接 EF ，分别与 BC ， AD 交于点G ， H ．求证： EG FH ． 19．有 4 张看上去无差别的卡片，上面分别写有数 1 ，2，5，8． （1）随机抽取一张卡片，则抽取到的数是偶数的概率为______； （2）随机抽取一张卡片后，放回并混在一起，再随机抽取一张，请用画树状图或列表 法，求抽取出的两数之差的绝对值大于 3 的概率． 20．如图，在平面直角坐标系中，已知点  1,5A  ，  3,1B  和  4,0C ，请按下列要 求画图并填空． （1）平移线段 AB ，使点 A 平移到点C ，画出平移后所得的线段 CD ，并写出点 D 的 坐标为______； （2）将线段 AB 绕点 A 逆时针旋转90 ，画出旋转后所得的线段 AE ，并直接写出 cos BCE 的值为______； （3）在 y 轴上找出点 F ，使 ABF 的周长最小，并直接写出点 F 的坐标为______． 21．已知关于 x 的一元二次方程  2 212 1 2 02x k x k     ． （1）求证：无论 k 为何实数，方程总有两个不相等的实数根； （2）若方程的两个实数根 1x ， 2x 满足 1 2 3x x  ，求 k 的值． 22．某电商积极响应市政府号召，在线销售甲、乙、丙三种农产品．已知1kg 乙产品的 售价比1kg 甲产品的售价多 5 元，1kg 丙产品的售价是1kg 甲产品售价的 3 倍，用 270 元购买丙产品的数量是用 60 元购买乙产品数量的 3 倍． （1）求甲、乙、丙三种农产品每千克的售价分别是多少元？ （2）电商推出如下销售方案：甲、乙、丙三种农产品搭配销售共 40kg ，其中乙产品的 数量是丙产品数量的 2 倍，且甲、丙两种产品数量之和不超过乙产品数量的 3 倍．请你 帮忙计算，按此方案购买 40kg 农产品最少要花费多少元？ 23．已知 ABC 内接于 O ， AB AC ， ABC 的平分线与 O 交于点 D ，与 AC 交于点 E ，连接CD 并延长与 O 过点 A 的切线交于点 F ，记 BAC   ． （1）如图 1，若 60  ， ①直接写出 DF DC 的值为______； ②当 O 的半径为 2 时，直接写出图中阴影部分的面积为______； （2）如图 2，若 60  ，且 2 3 DF DC  ， 4DE  ，求 BE 的长． 24．在平面直角坐标系中，已知抛物线  2 4 4 6 0y ax ax a a     与 x 轴交于 A ，B 两点（点 A 在点 B 的左侧），与 y 轴交于点C ，顶点为点 D ． （1）当 6a  时，直接写出点 A ， B ，C ， D 的坐标： A ______， B ______，C ______， D ______； （2）如图 1，直线 DC 交 x 轴于点 E ，若 4tan 3AED  ，求 a 的值和CE 的长； （3）如图 2，在（2）的条件下，若点 N 为OC 的中点，动点 P 在第三象限的抛物线上， 过点 P 作 x 轴的垂线，垂足为Q ，交 AN 于点 F ；过点 F 作 FH DE ，垂足为 H ．设 点 P 的横坐标为 t ，记 f FP FH  ． ①用含 t 的代数式表示 f ； ②设  5 0t m m    ，求 f 的最大值． 参考答案 1．A 【解析】 【分析】 根据具有相反意义的量进行书写即可． 【详解】 由题知：温度上升3℃，记作 3 ℃， ∴温度下降 2℃，记作 2 ℃， 故选：A． 【点睛】 本题考查了具有相反意义的量的书写形式，熟知此知识点是解题的关键． 2．B 【解析】 【分析】 已知 OE CD ， 40BOE   ，根据邻补角定义即可求出 AOC 的度数． 【详解】 ∵OE CD ∴ 90COE   ∵ 40BOE   ∴ 180° 180 90 40 50AOC COE EOB          故选：B 【点睛】 本题考查了垂直的性质，两条直线垂直，形成的夹角是直角；利用邻补角的性质求角的度数， 平角度数为 180°． 3．C 【解析】 【分析】 据合并同类项的法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变和 单项式的乘法法则，逐一判断即可. 【详解】 A：2a 和 3b 不是同类项，不能合并，故此选项错误； B： 2 2 23 9ab a b 故 B 错误； C： 2 3 6a b ab  正确； D： 22 2ab b ab 故 D 错误. 【点睛】 本题考查了合并同类项以及单项式的乘法的知识，解答本题的关键是熟练掌握合并同类项的 法则. 4．C 【解析】 【分析】 从左面看，所得到的图形形状即为所求答案． 【详解】 从左面可看到第一层为 2 个正方形，第二层为 1 个正方形且在第一层第一个的上方， 故答案为：C． 【点睛】 本题考查了三视图的知识，左视图是从物体的左面看得到的视图． 5．B 【解析】 【分析】 数据出现最多的为众数;将数据从小到大排列,最中间的 2 个数的平均数为中位数． 【详解】 6 出现次数最多, 故众数为: 6， 最中间的 2 个数为 6 和 6，中位数为 6+6 =62 ， 故选: B． 【点睛】 本题考查众数和中位数,需要注意,求解中位数前,一定要将数据进行排序． 6．D 【解析】 【分析】 先按照分式四则混合运算法则化简原式，然后将 x、y 的值代入计算即可． 【详解】 解：   3 2x xy x x y   =      x x y x y x x y    =x+y= 5 1 + 5 1 =2 5 ． 故答案为 D． 【点睛】 本题考查了分式的化简求值，根据分式四则混合运算法则化简分式是解答本题的关键． 7．C 【解析】 【分析】 根据题意，电流与电阻是反比例函数关系，根据图中给出的坐标即可求出该反比例函数解析 式． 【详解】 根据题意，电流与电阻是反比例函数关系，在该函数图象上有一点(6,8)， 故设反比例函数解析式为 I= k R ， 将(6,8)代入函数解析式中， 解得 k=48， 故 I= 48 R 故选 C． 【点睛】 本题主要考查反比例函数解析式的求解方法，掌握求解反比例函数解析式的方法是解答本题 的关键． 8．A 【解析】 【分析】 利用平移的规律:左加右减，上加下减.并用规律求函数解析式 2C ，再因为关于 x 轴对称的两 个抛物线，自变量 x 的取值相同，函数值 y 互为相反数，由此可直接得出抛物线 3C 的解析 式． 【详解】 解：抛物线 2 1 : 2 3C y x x   向左平移 1 个单位长度，得到抛物线 2C ：    2+1 2 +1 3  y x x ，即抛物线 2C ： 2 2y x  ; 由于抛物线 2C 与抛物线 3C 关于 x 轴对称，则抛物线 3C 的解析式为： 2 2y x   . 故选：A． 【点睛】 主要考查了函数图象的平移、对称，要求熟练掌握平移的规律:左加右减，上加下减.并用规 律求函数解析式以及关于 x 轴对称的两个抛物线，自变量 x 的取值相同，函数值 y 互为相反 数． 9．D 【解析】 【分析】 分点 P 在 AB 边上，如图 1，点 P 在 BC 边上，如图 2，点 P 在 CD 边上，如图 3，利用解直 角三角形的知识和三角形的面积公式求出相应的函数关系式，再根据相应函数的图象与性质 即可进行判断． 【详解】 解：当点 P 在 AB 边上，即 0≤x≤4 时，如图 1， ∵AP=x， 30BAD   ， ∴ 1 3,2 2PH x AH x  ， ∴ 21 1 3 3 2 2 2 8y x x x    ； 当点 P 在 BC 边上，即 4＜x≤10 时，如图 2， 过点 B 作 BM⊥AD 于点 M，则 1 32, 2 3, 42 2PH BM AB AM AB MH BP x        ， ∴  1 1 2 3 4 2 2 3 42 2y AH PH x x         ； 当点 P 在 CD 边上，即 10＜x≤12 时，如图 3， AD= 2 3 6 ， 12PH x  ， ∴       1 2 3 6 12 3 3 122y x x        ； 综上，y 与 x 的函数关系式是：         23 0 48 2 3 4 4 10 3 3 12 10 12 y x x y x x y x x                  ， 其对应的函数图象应为： ． 故选：D． 【点睛】 本题以直角梯形为载体，主要考查了动点问题的函数图象、一次函数和二次函数的图象与性 质以及解直角三角形等知识，属于常考题型，正确分类、列出相应的函数关系式是解题的关 键． 10．B 【解析】 【分析】 根据正方形性质和已知条件可知 BC=CD=5,再由旋转可知 DE=BF,设 DE=BF=x，则 CE=5-x， CF=5+x，然后再证明△ABG∽△CEF，根据相似三角形的性质列方程求出 x，最后求 CE 即 可． 【详解】 解：∵ 3BG  ， 2CG  ∴BC=BG+GC=2+3=5 ∵正方形 ABCD ∴CD=BC=5 设 DE=BF=x，则 CE=5-x，CF=5+x ∵AH⊥EF，∠ABG=∠C=90° ∴∠HFG+∠AGF=90°，∠BAG+∠AGF=90° ∴∠HFG=∠BAG ∴△ABG∽△CEF ∴ CE BG FC AB  ,即 5 3 5 5 x x   ，解得 x= 5 4 ∴CE=CD-DE=5- 5 4 =15 4 ． 故答案为 B． 【点睛】 本题考查了正方形的性质和相似三角形的判定与性质，根据相似三角形的性质列方程求出 DE 的长是解答本题的关键． 11． 61 10 【解析】 【分析】 先将 100 万写成 1000000，然后再写成 a×10n 的形式，其中 1≤|a|＜10，n 为 1000000 写成 a 时小时点向左移动的位数． 【详解】 解：100 万=1000000= 61 10 故答案为 61 10 ． 【点睛】 本题考查了科学记数法，将 1000000 写成 a×10n 的形式，确定 a 和 n 的值是解答本题的关键． 12． 81 【解析】 【分析】 题中数列的绝对值的比是-3，由三个相邻数的和是 567 ，可设三个数为 n，-3n，9n，据题 意列式即可求解． 【详解】 题中数列的绝对值的比是-3，由三个相邻数的和是 567 ，可设第一个数是 n，则三个数为 n， -3 n，9n 由题意：  n 3n 9n 567     ， 解得：n=-81， 故答案为：-81． 【点睛】 此题主要考查数列的规律探索与运用，一元一次方程与数字的应用，熟悉并会用代数式表示 常见的数列，列出方程是解题的关键． 13． 5 3( 1.6)3  【解析】 【分析】 如图（见解析），先在 Rt BCF 中，解直角三角形可求出 CF 的长，再根据等腰直角三角形 的判定与性质可得 DE 的长，从而可得 CE 的长，然后根据线段的和差即可得． 【详解】 如图，过 A 作 //AE BF ，交 DF 于点 E，则四边形 ABFE 是矩形 , 5 ,AB EF AE BF m AE EF     由图中数据可知， 3.4CD m ， 30CBF   ， 45DAE  ， 90F   在 Rt BCF 中， tan CFCBF BF   ，即 3tan305 3 CF    解得 5 3 ( )3CF m , 45AE EF DAE    Rt ADE  是等腰三角形 5DE AE m   5 3.4 1.6( )CE DE CD m      5 3 1.6( )3EF CF CE m     则 AB 的长为 5 3( 1.6)3 m 故答案为： 5 3( 1.6)3  ． 【点睛】 本题考查了解直角三角形的应用、等腰三角形的判定与性质等知识点，掌握解直角三角形的 方法是解题关键． 14．336 【解析】 【分析】 先根据 A 类的条形统计图和扇形统计图信息求出调查抽取的总人数，再求出每天做眼保健 操总时长超过 5 分钟且不超过 10 分钟的学生的占比，然后乘以 1200 即可得． 【详解】 调查抽取的总人数为10 10% 100  （人） C 类学生的占比为 41 100% 41%100   B 类学生的占比为100% 10% 41% 21% 28%    则1200 28% 336  （人） 即该校每天做眼保健操总时长超过 5 分钟且不超过 10 分钟的学生约有 336 人 故答案为：336． 【点睛】 本题考查了条形统计图和扇形统计图的信息关联等知识点，掌握理解统计调查的相关知识是 解题关键． 15． 3 1 2  【解析】 【分析】 如图（见解析），设 AB CD a  ，先根据直角三角形的面积公式、正方形的面积公式求出 1 2,S S 的值，再根据 1 2S S= 建立等式，然后根据 2 1 2S S m+ = 建立等式求出 a 的值，最后代入 求解即可． 【详解】 如图，由题意得： AC m ， BD n ， AB CD ， ABC 是直角三角形，且 ,m n 均为 正数 则大正方形的面积为 2 2AC m= 小正方形的面积为 2 2BD n= 设 ( 0)AB CD a a   则 2 2 2 1 14 4 22Rt ABDS S n AB BD n an n= + = 醋 + = + 2 2 14 4 22ACDS S CD AB a= = 醋 = 1 2S S = 2 22 2an n a + = 又 2 1 2S S m + = ，即 2 22S m= 2 24a m = 解得 2 ma  或 2 ma = - （不符题意，舍去） 将 2 ma  代入 2 22 2an n a+ = 得： 2 2 2 mmn n+ = 两边同除以 2 2 m 得： 22 2( ) 1n n m m + = 令 0n xm = > 则 22 2 1x x+ = 解得 3 1 2x  或 3 1 02x - -= < （不符题意，舍去） 即 n m 的值为 3 1 2  故答案为： 3 1 2  ． 【点睛】 本题考查了一元二次方程与几何图形、勾股定理、三角形全等的性质等知识点，理解题意， 正确求出 1 2,S S 的值是解题关键． 16． 13 2 【解析】 【分析】 先作 AG x 轴于点 G，作 BH x 轴于点 H，证明 AOG OBH△ △ ，利用 2 3 AC BD  ， 同时设出点 A 的坐标，表示出 OH，BH 的长度，求出 k 的值，设直线 EF 的解析式为 y n ， 表示点 E，F 的坐标，求出 EF 的长度，可求得 OEF 的面积． 【详解】 作 AG x 轴于点 G，作 BH x 轴于点 H，如图所示： ∵ AOG OAG AOG BOG       即 OAG BOH   ∴ AOG OBH△ △ ∴ 2 3 AO OG AG AC OB BH OH BD     设点 A 的坐标为 4( , )m m 则 4,OG m AG m   ∴ 6 3, 2 mOH BHm   ∴ 6 3| | 92 mk OH BH m      ∵ ky x  的图象在第二，四象限 ∴ 9k   设直线 EF 的解析式为： y n 则 9 4( , ), ( , )F n E nn n  ∴ 4 9 13( )EF n n n     ∴ 1 1 13 13| |2 2 2OEF FS EF y nn      △ 故答案为：13 2 ． 【点睛】 本题考查了反比例函数与几何图形的综合，快速找到相似三角形求出 k 的值，是解题的关键． 17． 2 ． 【解析】 【分析】 先计算立方根、绝对值运算、特殊角的三角函数值、零指数幂，再计算实数的混合运算即可． 【详解】 原式 32 3 1 2 12       2 3 1 3 1      2  ． 【点睛】 本题考查了立方根、绝对值运算、特殊角的三角函数值、零指数幂等知识点，熟记各运算法 则是解题关键． 18．证明见解析． 【解析】 【分析】 先根据平行四边形的性质可得 //AB CD ， ABC CDA   ，再根据平行线的性质、邻补角 的定义可得 E F   ， EBG FDH   ，然后根据三角形全等的判定定理与性质即可得 证． 【详解】 ∵四边形 ABCD 为平行四边形 ∴ //AB CD ， ABC CDA   ∴ E F   ，180 180ABC CDA   EBG FDH   在 BEG 和 DFH 中， E F BE DF EBG FDF         ∴ ( )BEG DFH ASA  ∴ EG FH ． 【点睛】 本题考查了平行四边形的性质、平行线的性质、邻补角的定义、三角形全等的判定定理与性 质等知识点，熟练掌握平行四边形的性质，正确找出全等三角形是解题关键． 19．（1） 1 2 ;（2） 3 8 【解析】 【分析】 （1）直接利用概率公式进行计算即可； （2）列表展示所有 16 种等可能的结果数,再找出两次抽取的卡片上两数之差的绝对值大于 3 结果数,然后根据概率公式求解． 【详解】 解：（1）抽取到的数为偶数的概率为 P= 2 1 4 2  ． （2）列表如下： 第 1 次 第 2 次 1 2 5 8 1  1, 1   2, 1  5, 1  8, 1 2 ( )1,2-  2,2  5,2  8,2 5  1,5  2,5  5,5  8,5 8  1,8  2,8  5,8  8,8 ∵差的绝对值有 16 种可能，绝对值大于 3 的有 6 种可能， ∴差的绝对值大于 3 的概率 6 3 16 8P   ． 【点睛】 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果 n,再从中选出 符合事件 A 或 B 的结果数目 m,然后利用概率公式计算事件 A 或事件 B 的概率． 20．（1）（2，-4） （2） 5 5 （3）（0,4） 【解析】 【分析】 （1）平移线段 AB，使 A 点平移到 C 点，可以知道 A 点是向右平移 5 个单位，向下平移 5 个单位，故可以确定 D 点坐标． （2）根据 B、C、E 三点坐标，连接 BE，可以判断出△BCE 为直角三角形，故可求解 cos BCE 的值． （3）过 A 点做 y 轴的对称点 A’，连接 A’B，与 y 轴的交点即为 F 点．此时△ABF 的周长 最小，通过求解函数解析式确认点Ｆ的坐标． 【详解】 解：(1)如图所示：平移线段 AB，使 A 点平移到 C 点，可以知道 A 点是向右平移 5 个单位， 再向下平移 5 个单位，根据题意可知，B 点(-3,1)平移到 D 点，故可以确定点 D 的坐标． 点 D 的坐标为  2, 4 ； (2)如图所示： 根据题意，AE 是线段 AB 围绕点 A 逆时针旋转 90°得到，故 AB=AE，不难算出点 E 的坐标 为(3,3)．连接 BE，根据 B、C、E 三点坐标算出 BC= 5 2 、EC= 10 、BE= 2 10 ，故 2 2 2BE EC BC  ,可以判断出△BEC 为直角三角形． 故 5cos 5BCE EC BC   (3)如图所示： 过 A 点做 y 轴的对称点 A’，连接 A’B，与 y 轴的交点即为 F 点．故可知 A’的坐标为(1,5)， 点 B 的坐标为(-3,1),设 A’B 的函数解析式为 y=kx+b，将(1,5)，(-3,1)代入函数解析中解得 k=1， b=4，则函数解析式为 y=x+4,则 F 点坐标为(0,4), 故点 F 的坐标为(0,4)． 【点睛】 （1）本题主要考查平移，洞察点 A 是如何平移到点 C，是求出 D 点坐标的关键．（2）连接 BE，根据 B、C、E 三点坐标判断出△BCE 是直角三角形，就不难算出 cos BCE 的值．（3） 本题通过做 A 点的对称点 A’，连接 A’B，找到 A’B 与 y 轴的交点 F 是解答本题的关键． 21．（1）见解析 （2）0，-2 【解析】 【分析】 （1）根据根的判别式即可求证出答案； （2）可以根据一元二次方程根与系数的关系得 k 与的 1x 、 2x 的关系式，进一步可以求出答 案. 【详解】 (1)证明：∵  2 2 212 1 4 2 2 4 92k k k k             22 1 7k   ， ∵无论 k 为何实数，  22 1 0k   ， ∴  22 1 7 0k     ， ∴无论 k 为何实数，方程总有两个不相等的实数根； (2)由一元二次方程根与系数的关系得： 1 2 2 1x x k   ， 2 1 2 1 22x x k  ， ∵ 1 2 3x x  ， ∴ 2 1 2 9x x  ， ∴ 2 1 2 1 24 9x x x x   ， ∴ 2 212 1 4 2 92k k        ，化简得： 2 2 0k k  ， 解得 0k  ， 2 ． 【点睛】 本题主要考查根的判别式和根与系数的关系，熟练掌握概念和运算技巧即可解题. 22．（1）甲、乙、丙三种农产品每千克的售价分别是 5 元、10 元、15 元；（2）按此方案购 买 40kg 农产品最少要花费 300 元． 【解析】 【分析】 （1）设1kg 甲产品的售价为 x 元，先表示出1kg 乙产品的售价和1kg 丙产品的售价，再根 据“用 270 元购买丙产品的数量是用 60 元购买乙产品数量的 3 倍”建立方程，然后求解即 可得； （2）设 40kg 的甲、乙、丙三种农产品搭配中，丙种农产品有 mkg ，先求出乙种农产品的 数量和甲种农产品的数量，再根据题干三种农产品间的数量关系列出不等式求出 m 的取值 范围，然后根据（1）的结论得出所需费用关于 m 的函数关系式，最后利用一次函数的性质 即可得． 【详解】 （1）设1kg 甲产品的售价为 x 元，则1kg 乙产品的售价为  5x 元，1kg 丙产品的售价为 3x 元 由题意得： 270 60 33 5x x   解得： 5x  经检验， 5x  是所列分式方程的解，也符合题意 则 5 10 x ，3 15x  答：甲、乙、丙三种农产品每千克的售价分别是 5 元、10 元、15 元； （2）设 40kg 的甲、乙、丙三种农产品搭配中，丙种农产品有 mkg ，则乙种农产品有 2mkg ， 甲种农产品有  40 3m kg 由题意得： 40 3 3 2m m m    解得 5m  设按此销售方案购买 40kg 农产品所需费用 y 元 则  5 40 3 10 2 15 20 200y m m m m       ∵在 5m  范围内， y 随 m 的增大而增大 ∴当 5m  时， y 取得最小值，最小值为 20 5 200 300   （元） 答：按此方案购买 40kg 农产品最少要花费 300 元． 【点睛】 本题考查了分式方程的实际应用、一次函数的实际应用、一元一次不等式的应用等知识点， 依据题意，正确列出方程和函数的解析式是解题关键． 23．（1）① 1 2 ； ② 3 3 2 2 3  ；（2）5 【解析】 【分析】 （1）①连接 AD，连接 AO 并延长交 BC 于 H 点，根据题意先证明△ABC 是等边三角形， 再得到∠AFD 为直角，利用含 30°的直角三角形即可求解；②根据割补法即可求解阴影部分 面积； （2）连接 AD ，连接 AO 并延长交 O 于点 H ，连接 DH ，根据题意先证明 ADF ADE≌V V ，得到 4DF DE  ，再求出 6DC  ，根据 DCE DBC△ △∽ ，得到 CD DE DB CD  ，即可求出 BD，从而求出 BE 的长． 【详解】 解：（1）① 60BAC     ， AB AC ∴△ABC 是等边三角形， ∵BD 平分∠ABC， ∴∠DBC= 1 2 ∠ABC=30°， ∵∠BDC=∠BAC=60° ∴∠BCD=180°-∠DBC-∠BDC=90° ∴BD 是直径， ∴∠BAD=90°，CD=AD 连接 AO 并延长交 BC 于 H 点， ∵AO=BO ∴∠BAH=∠ABO=30°， ∴∠AHB=180°-∠BAH-∠ABC=90° ∴AH⊥BC ∵AF 是 O 的切线 ∴AF⊥AH ∴四边形 AHCF 是矩形 ∴AF⊥CF ∵∠ADB=∠BDC=60° ∴∠ADF=180°-∠ADB-∠BDC=60° ∴∠FAD=90°-∠ADF=30° ∴ 1 2 DF DF DC AD   ； ②∵半径为 2， ∴AO=OD=2， ∵∠DBC=30°， ∴CD= 1 2 BD=2=AD， ∴DF= 1 2 AD=1, ∴AF= 2 2 2 22 1 3AD DF    , ∵∠AOB=180°-2∠ABO=120°， ∴∠AOD=180°-∠AOB=60°， ∴ 2 21 60 1 60 2 3 3 2( ) (2 1) 32 360 2 360 2 3AODF AOD AOS S S AO DF AF                  梯形 扇形阴影 ﹔ 故答案为：① 1 2 ； ② 3 3 2 2 3  ； （2）如图，连接 AD ，连接 AO 并延长交 O 于点 H ，连接 DH ，则 90ADH   ， ∴ 90DAH DHA    ． ∵ AF 与 O 相切， ∴ 90DAH DAF FAO      ． ∴ DAF DHA   ． ∵ BD 平分 ABC ， ∴ ABD CBD   ． ∴ DHA DAC   ， ∴ DAF DAC   ． ∵ AB AC ， ∴ AABC CB ∠ ． ∵四边形 ABCD 内接于 O ， ∴ 180ABC ADC     ． 又∵ 180ADF ADC   ， ∴ ADF ABC   ． 又∵ ADB ACB ABC     ， ∴ ADF ADB   ． 又∵ AD 公共， ∴  ASAADF ADE≌△ △ ， ∴ 4DF DE  ． ∵ 2 3 DF DC  ， ∴ 6DC  ． ∵ DCE ABD DBC     ， CDE 公共， ∴ DCE DBC△ △∽ ． ∴ CD DE DB CD  ，即 6 4 6DB  ， ∴ 9DB  ． ∴ 5BE DB DE   ． 【点睛】 此题主要考查切线的判定与性质综合，解题的关键是熟知切线的性质、等边三角形的判定与 性质及相似三角形的判定与性质． 24．（1） 3,0 ， 1,0 ， 0,18 ， 2, 6  ；（2）2 3 ； 25 6 ；（3）① 22 843 3f t t    ； ② 26 3 ． 【解析】 【分析】 （1）求出 0y  时，x 的值可得点 A、B 的坐标，求出 0x  时，y 的值可得点 C 的坐标， 将二次函数的解析式化为顶点式即可得点 D 的坐标； （2）先求出顶点 D 的坐标，从而可得 DK、OK 的长，再利用正切三角函数可得 EK、OE、 OC 的长，从而可得出点 C 的坐标，然后将点 C 的坐标代入二次函数的解析式可得 a 的值， 利用勾股定理可求出 CE 的长； （3）①如图，先利用待定系数法求出直线 AN 的解析式，从而可得点 F 的坐标，由此可得 出 PF 的长，再利用待定系数法求出直线 CE 的解析式，从而可得点 J 的坐标，由此可得出 FJ 的长，然后根据相似三角形的判定与性质可得 FH FJ OE CE  ，从而可得 FH 的长，最后根据 f 的定义即可得； ②先将 f 的表达式化为顶点式，从而得出其增减性，再利用二次函数的性质即可得． 【详解】 （1）当 6a  时， 26 24 18y x x   当 0y  时， 26 24 18 0x x   ，解得 1x   或 3x   则点 A 的坐标为 ( 3,0)A  ，点 B 的坐标为 ( 1,0)B  当 0x  时， 18y  则点 C 的坐标为 (0,18)C 将 26 24 18y x x   化成顶点式为 26( ) 62y x   则点 D 的坐标为 ( 2, 6)D   故答案为： 3,0 ， 1,0 ， 0,18 ， 2, 6  ； （2）如图，作 DK x 轴于点 K 将 2 4 4 6y ax ax a    化成顶点式为 2( 2) 6y a x   则顶点 D 的坐标为 ( 2, 6)D   ∴ 6DK  ， 2OK  在 Rt DKE 中， tan DKAED EK   ，即 6 4 3EK  解得 9 2EK  9 522 2KOE EK O    在 Rt COE△ 中， tan OCAED OE  ，即 4 5 3 2 OC  解得 10 3OC  10(0, )3C  ， 2 2 2 210 5( ) ( )3 2 2 5 6CE OC OE     将点 10(0, )3C  代入 2 4 4 6y ax ax a    得： 104 6 3a    解得 2 3a  ； （3）①如图，作 FP 与 ED 的延长线交于点 J 由（2）可知， 2 3a  ， 100, 3C     ∴ 22 8 10 3 3 3y x x   当 0y  时， 22 8 10 03 3 3x x   ，解得 5x   或 1x  ∴  5,0A  ，  10B , NQ 为 OC 的中点 ∴ 50, 3N     设直线 AN 的解析式为 1 1y k x b  将点  5,0A  ， 50, 3N     代入得： 1 1 1 5 0 5 3 k b b      ，解得 1 1 1 3 5 3 k b       则直线 AN 的解析式为 1 5 3 3y x   ∵ 22 8 10, 3 3 3P t t t     ∴ 1 5, 3 3F t t     ∴ 2 21 5 2 8 10 2 5( ) 33 3 3 3 3 3 3PF t t t t t          由（2）知， 2 5OE   5 ,02E      ， 100, 3C     设直线 CE 的解析式为 2 2y k x b  将点 5 ,02E      ， 100, 3C     代入得： 2 2 2 5 02 10 3 k b b       ，解得 2 2 4 3 10 3 k b      则直线 CE 的解析式为 4 10 3 3y x  ∴ 4 10, 3 3J t t    ∴ 1 5 4 10 5 5( )3 3 3 3 3 3FJ t t t        ∵ FH DE ， //JF y 轴 ∴ 90FHJ EOC     ， FJH ECO   ∴ FJH ECO  ∴ FH FJ OE CE  ，即 5 5 3 2 2 6 5 3 5 tFH    解得 1FH t   ∴  22 53 13 3f PF FH t t t         即 22 843 3f t t    ； ②将 22 843 3f t t    化成顶点式为  22 2633 3tf     由二次函数的性质可知，当 3t   时， f 随 t 的增大而增大；当 3t   时， f 随 t 的增大而 减小  5 0t m m    5 0m   因此，分以下两种情况： 当 5 3m    时 在 5 t m   内， f 随 t 的增大而增大 则当t m 时， f 取得最大值，最大值为  22 2633 3m   又 当 5 3m    时，  2 02 33 m    22 26 2633 3 3m    当 3 0m   时 在 5 3t    内， f 随 t 的增大而增大；在 3 t m   内， f 随 t 的增大而减小 则当 3t   时， f 取得最大值，最大值为 26 3 综上， f 的最大值为 26 3 ． 【点睛】 本题考查了利用待定系数法求二次函数的表达式、二次函数的图象与性质、正切三角函数、 相似三角形的判定与性质等知识点，较难的是题（3）①，通过作辅助线，构造相似三角形 求出 FH 的长是解题关键．