苏教版数学九年级上册课件2-4圆周角（3） 11页

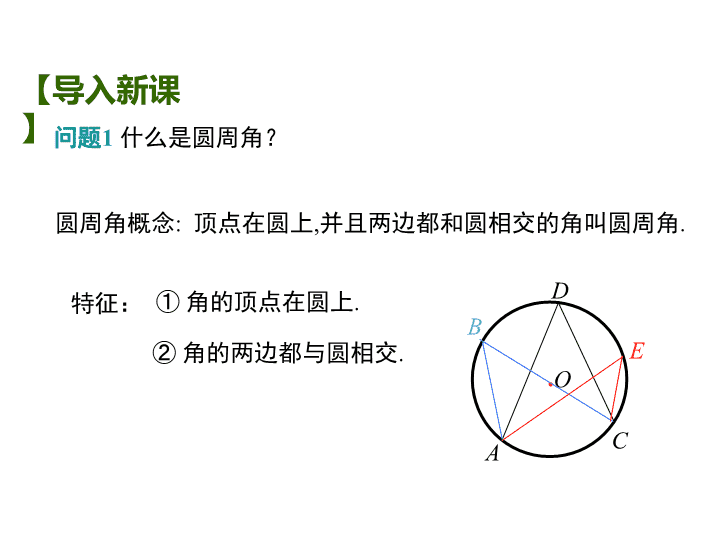
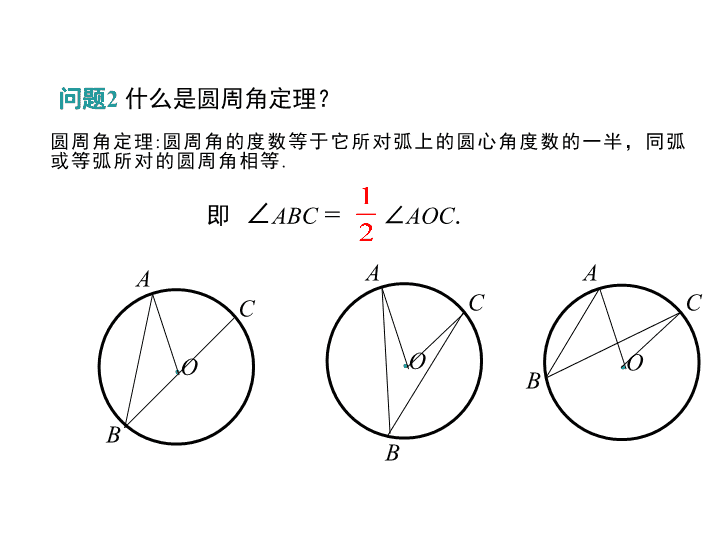
2.4 圆周角（3） 问题1 什么是圆周角？ 特征： ① 角的顶点在圆上. ② 角的两边都与圆相交. 圆周角概念: 顶点在圆上,并且两边都和圆相交的角叫圆周角. ●O B A C D E 【导入新课】 问题2 什么是圆周角定理？ 圆周角定理 :圆周角的度数等于它所对弧上的圆心角度数的一半，同弧 或等弧所对的圆周角相等 . ●O A B C ●O A B C ●O A B C 即 ∠ABC = ∠AOC. 圆内接四边形及其性质 一个四边形的4个顶点都在同一个圆上，这个四边形叫做 圆的内接四边形，这个圆叫做四边形的外接圆. O A C D B 【讲授新课】 定理：圆内接四边形的对角互补. 由于∠A是∠DCE的补角∠BCD的对角（简称∠DCE 的内对角），于是我们得到圆内接四边形的性质： 【例题讲解】 如图,已知点E是圆内接四边形ABCD的边BA延长线 上的一点,BD=CD,且∠EAD=55°,则∠BDC=　　　 　.  解:由圆内接四边形的性质,得∠C+∠DAB=180°. ∵∠EAD+∠DAB=180°, ∴∠C=∠EAD=55°. 又∵BD=CD,∴∠DBC=∠C. ∴∠BDC=180°-2∠C=180°-2×55°=70°. 如图所示,A,B,C,D是圆上的四个点,AB,DC的延长线 交于点E,若BC=BE,确定△ADE的形状,并说明理由. 解:△ADE是等腰三角形.理由如下: ∵A,B,C,D是圆上的四个点, ∴∠A=∠BCE. ∵BC=BE,∴∠E=∠BCE. ∴∠A=∠E,∴△ADE是等腰三角形. 1.在⊙ O中，∠CBD=30°，∠BDC=20°,求∠A. O A B D C 解：∵∠CBD=30°，∠BDC=20° ∴∠C=180°-∠CBD-∠BDC=130° ∴∠A=180°-∠C=50°（圆内接四边形对角互补） 【练习】 变式：已知∠OAB等于40°,求∠C 的度数. A B C O D . 90 40 50 . 180 50 130 . AO D D BD ABD OAB ADB C                  解：延长 至 ，交圆于点 ，连接 ， ， 2.判断. （1）等弧所对的圆周角相等；（ ） （2）相等的弦所对的圆周角也相等；（ ） （3）90°的角所对的弦是直径；（ ） （4）同弦所对的圆周角相等.（ ） × × × × 2.圆内接四边形的性质定理：圆内接四边形的对角互补. 1.一个四边形的4个顶点都在同一个圆上，这个四边形叫 做圆的内接四边形，这个圆叫做四边形的外接圆. 【小结】