初中数学中考复习课件章节考点专题突破：第六章 图形性质2-24 圆的基本性质 21页

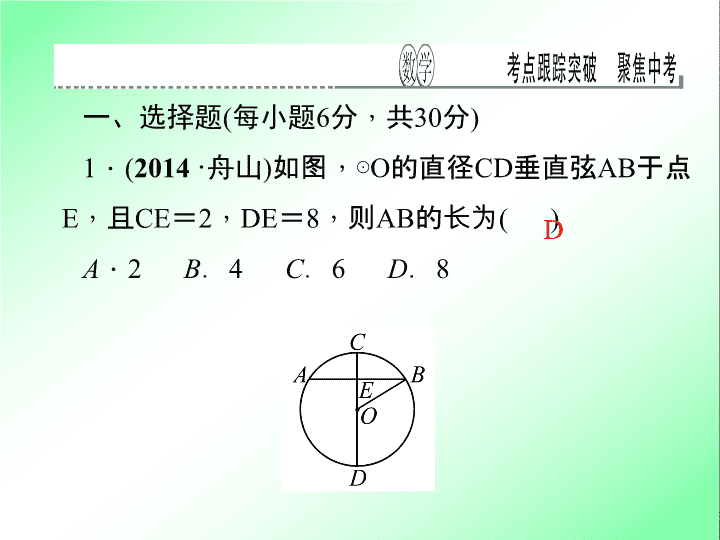
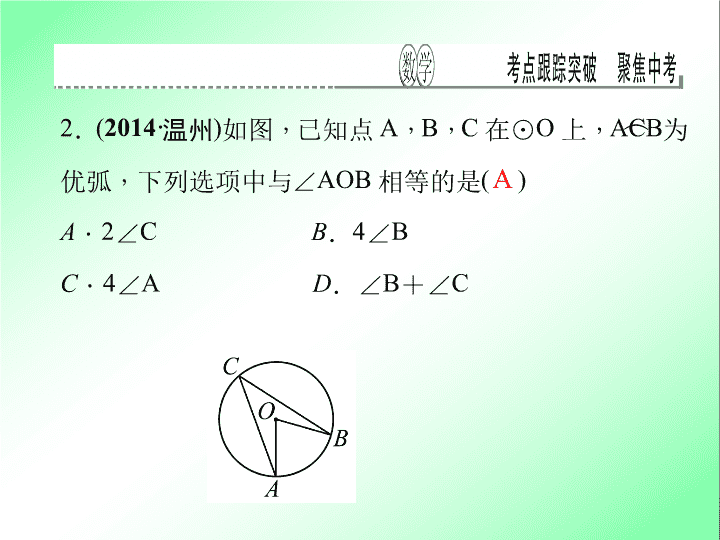
考点跟踪突破 24 　圆的基本性质 一、选择题 ( 每小题 6 分 ， 共 30 分 ) 1 ． ( 2014 · 舟山 ) 如图 ， ⊙ O 的直径 CD 垂直弦 AB 于点 E ， 且 CE ＝ 2 ， DE ＝ 8 ， 则 AB 的长为 ( ) A ． 2 B ． 4 C ． 6 D ． 8 D 2 ． ( 2014· 温州 ) 如图 ， 已知点 A ， B ， C 在 ⊙ O 上 ， ACB ︵ 为 优弧 ， 下列选项中与 ∠ AOB 相等的是 ( ) A ． 2 ∠ C B ． 4 ∠ B C ． 4 ∠ A D ． ∠ B ＋ ∠ C A 3 ． ( 2014· 毕节 ) 如图是以 △ ABC 的边 AB 为直径的半圆 O ， 点 C 恰好在半圆上 ， 过点 C 作 CD ⊥ AB 交 AB 于点 D. 已知 cos ∠ ACD ＝ 3 5 ， BC ＝ 4 ， 则 AC 的长为 ( ) A ． 1 B . 20 3 C ． 3 D . 16 3 D 4 ． ( 2014· 兰州 ) 如图 ， CD 是 ⊙ O 的直径 ， 弦 AB ⊥ CD 于 点 E ， 连接 BC ， BD ， 下列结论中不一定正确的是 ( ) A ． AE ＝ BE B . AD ︵ ＝ BD ︵ C ． OE ＝ DE D ． ∠ DBC ＝ 90 ° C 5 ． ( 2014· 孝感 ) 如图 ， 在半径为 6 cm 的 ⊙ O 中 ， 点 A 是劣 弧 BC ︵ 的中点 ， 点 D 是优弧 BC ︵ 上一点 ， 且 ∠ D ＝ 30 ° ， 下 列四个结论： ① OA ⊥ BC ； ② BC ＝ 6 3 cm ； ③ sin ∠ AOB ＝ 3 2 ； ④ 四边形 ABOC 是菱形 ． 其中正确的序号是 ( ) A ． ①③ B ． ①②③④ C ． ②③④ D ． ①③④ B 二、填空题 ( 每小题 6 分 ， 共 30 分 ) 6 ． ( 2014 · 广东 ) 如图 ， 在 ⊙ O 中 ， 已知半径为 5 ， 弦 AB 的长为 8 ， 那么圆心 O 到 AB 的距离为 ____ ． 3 7 ． ( 2014 · 巴中 ) 如图 ， 已知 A ， B ， C 三点在 ⊙ O 上 ， AC ⊥ BO 于点 D ， ∠ B ＝ 55° ， 则 ∠ BOC 的度数是 ． 70° 8 ． ( 2014 · 泰安 ) 如图， AB 是半圆的直径 ， 点 O 为圆心 ， OA ＝ 5 ， 弦 AC ＝ 8 ， OD ⊥ AC ， 垂足为点 E ， 交 ⊙ O 于点 D ， 连接 BE. 设 ∠ BEC ＝ α ， 则 sin α 的值 为 ． 9 ． ( 2014 · 宁波 ) 如图 ， 半径为 6 cm 的 ⊙ O 中 ， C ， D 为直径 AB 的三等分点 ， 点 E ， F 分别在 AB 两侧的半圆上 ， ∠ BCE ＝ ∠ BDF ＝ 60° ， 连接 AE ， BF ， 则图中两个阴影部分的面积为 ____ cm 2 . 10 ． 如图 ， 在半径为 5 的⊙ O 中 ， 弦 AB ＝ 6 ， 点 C 是优弧上一点 ( 不与 A ， B 重合 ) ， 则 cos C 的值为 ____ ． 三、解答题 ( 共 40 分 ) 11 ． (8 分 ) ( 2014 · 湖州 ) 已知在以点 O 为圆心的两个同心圆中 ， 大圆的弦 AB 交小圆于点 C ， D( 如图 ) ． (1) 求证： AC ＝ BD ； (2) 若大圆的半径 R ＝ 10 ， 小圆的半径 r ＝ 8 ， 且圆 O 到直线 AB 的距离为 6 ， 求 AC 的长． 12 ． ( 8 分 ) ( 2013· 邵阳 ) 如图所示 ， 某窗户由矩形和弓形组 成 ． 已知弓形的跨度 AB ＝ 3 m ， 弓形的高 EF ＝ 1 m ． 现计 划安装玻璃 ， 请帮工程师求出 AB ︵ 所在圆 O 的半径 ． 13 ． (8 分 ) ( 2012 · 沈阳 ) 如图 ， ⊙ O 是 △ ABC 的外接圆 ， AB 是 ⊙ O 的直径 ， D 为 ⊙ O 上一点 ， OD ⊥ AC ， 垂足为点 E ， 连接 BD. (1) 求证： BD 平分 ∠ ABC ； (2) 当 ∠ ODB ＝ 30° 时 ， 求证： BC ＝ OD. 解： ( 1 ) ∵ OD ⊥ AC ， OD 为半径 ， ∴ CD ︵ ＝ AD ︵ . ∴∠ CBD ＝ ∠ ABD. ∴ BD 平分 ∠ ABC ( 2 ) ∵ OB ＝ OD ， ∠ ODB ＝ 30 ° ， ∴∠ OBD ＝ ∠ ODB ＝ 30 ° . ∴∠ AOD ＝ ∠ OBD ＋ ∠ ODB ＝ 30 ° ＋ 30 ° ＝ 60 ° . 又 ∵ OD ⊥ AC 于点 E ， ∴∠ OEA ＝ 90 ° . ∴∠ A ＝ 90 ° － 60 ° ＝ 30 ° . 又 ∵ AB 为 ⊙ O 的直径 ， ∴∠ ACB ＝ 90 ° . ∴ 在 Rt △ ACB 中 ， BC ＝ 1 2 AB. ∵ OD ＝ 1 2 AB ， ∴ BC ＝ OD 14 ． (8 分 ) ( 2013 · 温州 ) 如图 ， AB 为 ⊙ O 的直径 ， 点 C 在 ⊙ O 上 ， 延长 BC 至点 D ， 使 DC ＝ CB ， 延长 DA 与 ⊙ O 的另一个交点为点 E ， 连接 AC ， CE. (1) 求证： ∠ B ＝ ∠ D ； 证明：∵ AB 为⊙ O 的直径 ， ∴∠ ACB ＝ 90° ， ∴ AC⊥BC ， ∵ DC ＝ CB ， ∴ AD ＝ AB ， ∴∠ B ＝∠ D (2) 若 AB ＝ 4 ， BC － AC ＝ 2 ， 求 CE 的长． 15 ． ( 8 分 ) ( 2014· 武汉 ) 如图 ， AB 是 ⊙ O 的直径 ， C ， P 是 AB ︵ 上两点 ， AB ＝ 13 ， AC ＝ 5. ( 1 ) 如图 ① ， 若点 P 是 AB ︵ 的中点 ， 求 PA 的长； ( 2 ) 如图 ② ， 若点 P 是 CB ︵ 的中点 ， 求 PA 的长 ． 解： (1) 如图 ① 所示 ， 连接 PB ， ∵ AB 是 ⊙ O 的直径且 P 是 AB ︵ 的中点 ， ∴∠ PAB ＝ ∠ PBA ＝ 45 ° ， ∠ APB ＝ 90 ° ， 又 ∵ 在等腰三角形 △ ABP 中有 AB ＝ 13 ， ∴ PA ＝ AB 2 ＝ 13 2 ＝ 13 2 2 ( 2) 如图 ② 所示：连接 BC ， OP 相交于 M 点 ， 作 PN ⊥ AB 于点 N ， ∵ P 点为弧 BC 的 中点 ， ∴ OP ⊥ BC ， ∠ OMB ＝ 90 ° ， 又因为 AB 为直径 ∴∠ ACB ＝ 90 ° ， ∴∠ ACB ＝ ∠ OMB ， ∴ OP ∥ AC ， ∴∠ CAB ＝ ∠ POB ， 又因为 ∠ ACB ＝ ∠ ONP ＝ 90 ° ， ∴△ ACB ∽△ ONP ， ∴ AB OP ＝ AC ON ， 又 ∵ AB ＝ 13 ， AC ＝ 5 ， OP ＝ 13 2 ， 代入得 ON ＝ 5 2 ， ∴ AN ＝ OA ＋ ON ＝ 9 ， ∴ 在 Rt △ OPN 中 ， 有 NP 2 ＝ OP 2 － ON 2 ＝ 36 ， 在 Rt △ ANP 中 ， 有 PA ＝ AN 2 ＋ NP 2 ＝ 117 ＝ 3 13 ， ∴ PA ＝ 3 13