2021年九年级中考数学复习《一次函数与几何综合题型》能力提升练习 8页

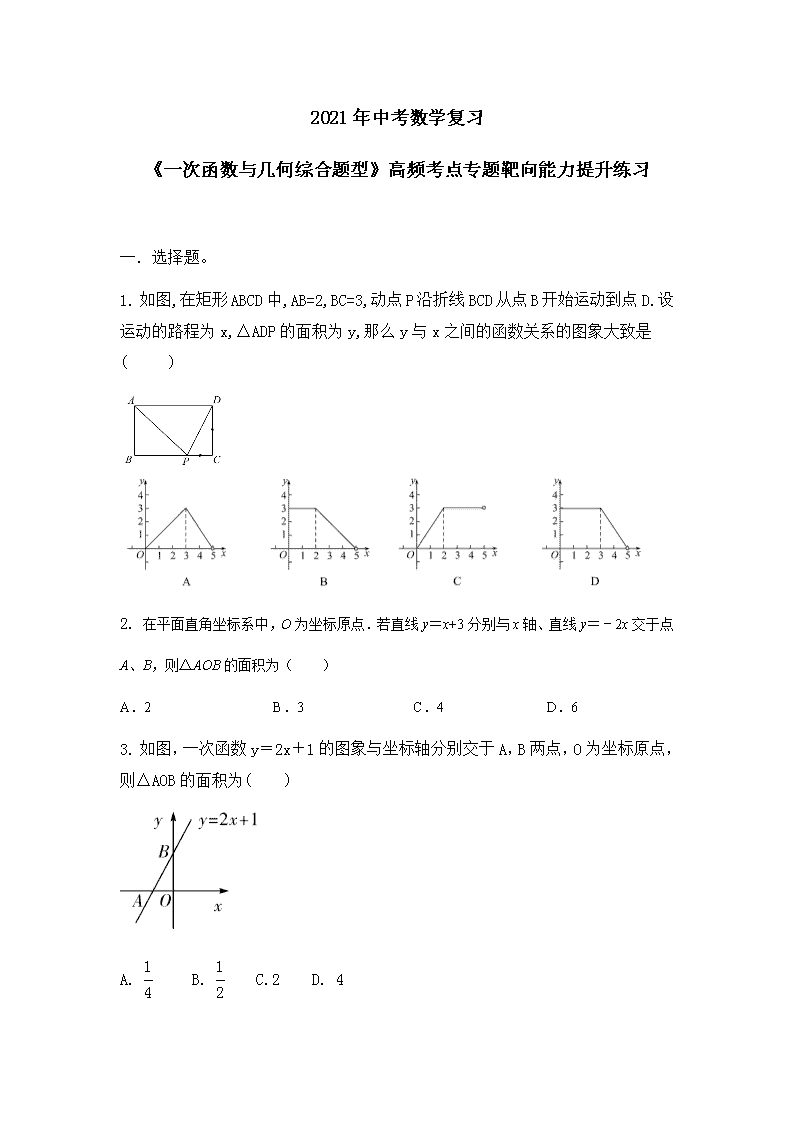
2021 年中考数学复习 《一次函数与几何综合题型》高频考点专题靶向能力提升练习 一．选择题。 1. 如图,在矩形 ABCD 中,AB=2,BC=3,动点 P 沿折线 BCD 从点 B 开始运动到点 D. 设运动的路程为 x,△ADP 的面积为 y,那么 y 与 x 之间的函数关系的图象大致是 ( ) 2. 在平面直角坐标系中，O 为坐标原点．若直线 y＝x+3 分别与 x 轴、直线 y＝﹣2x 交于点 A、B，则△AOB 的面积为（ ） A．2 B．3 C．4 D．6 3. 如图，一次函数 y＝2x＋1 的图象与坐标轴分别交于 A，B 两点，O 为坐标原 点，则△AOB 的面积为( ) A. 1 4 B. 1 2 C.2 D. 4 4.如图,一直线与两坐标轴的正半轴分别交于 A,B 两点,P 是线段 AB 上任意一点 (不包括端点),过点 P 分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为 8, 则该直线的函数表达式是( ) A.y=-x+4 B.y=x+4 C.y=x+8 D.y=-x+8 5. 如图，若菱形 AOBC 的顶点 A(－3，4)，则 A，B 两点所在直线的表达式为( ) A. y＝1 2 x＋5 2 B. y＝－1 2 x＋5 2 C. y＝1 2 x－5 2 D. y＝－1 2 x－5 2 二．填空题. 6. 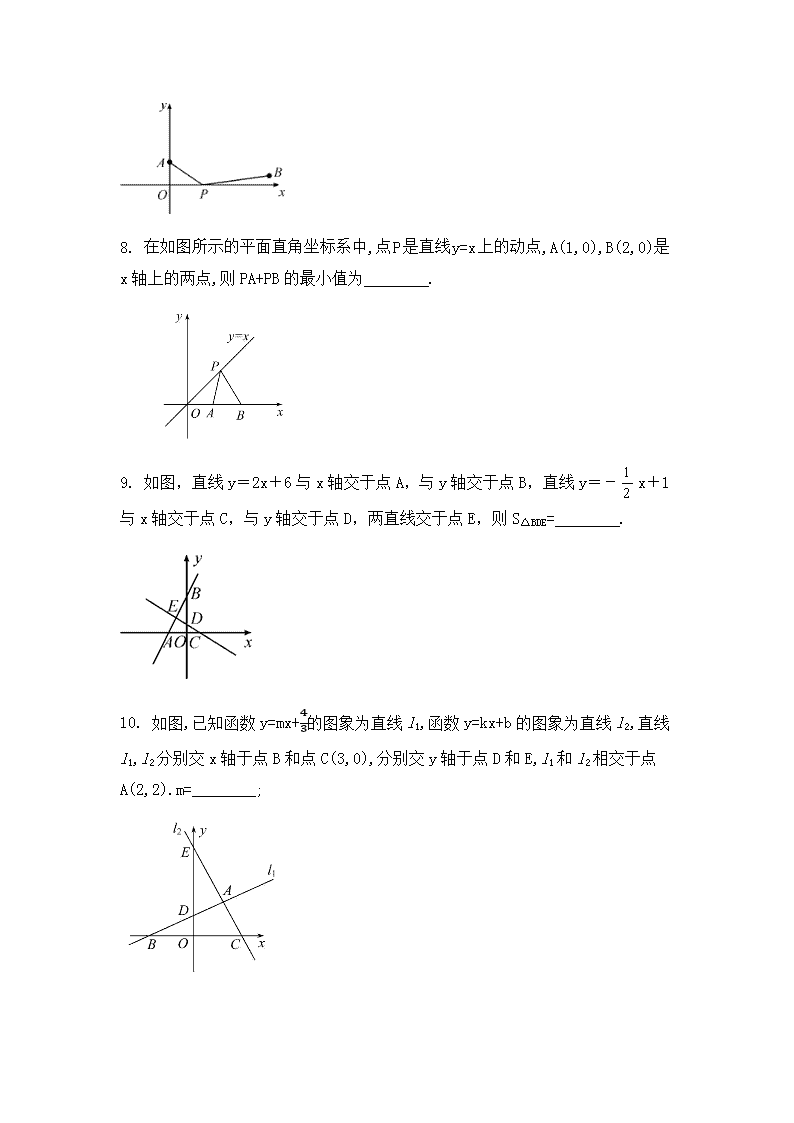如图，正方形 OBAC 中，O(0，0)，A(－2，2)，B，C 分别在 x 轴、y 轴上，D(0， 1)，CE⊥BD 交 BD 延长线于点 E，则点 E 的坐标为 ． 7.如图，在平面直角坐标系中，A(0，1)，B(3， 1 2 )，P 为 x 轴上一动点，则 PA ＋PB 最小时点 P的坐标为________． 8. 在如图所示的平面直角坐标系中,点 P 是直线 y=x 上的动点,A(1,0),B(2,0) 是 x 轴上的两点,则 PA+PB 的最小值为 . 9. 如图，直线 y＝2x＋6 与 x 轴交于点 A，与 y 轴交于点 B，直线 y＝－ 1 2 x＋1 与 x 轴交于点 C，与 y 轴交于点 D，两直线交于点 E，则 S△BDE= . 10. 如图,已知函数 y=mx+ 4 3 的图象为直线 l1,函数 y=kx+b 的图象为直线 l2,直线 l1,l2 分别交 x 轴于点 B 和点 C(3,0),分别交 y 轴于点 D 和 E,l1 和 l2 相交于点 A(2,2).m=________; 11. 如图，直线 y＝－ 4 3 x＋8 分别交 x 轴、y 轴于 A，B 两点，线段 AB 的垂直平 分线分别交 x 轴、y 轴于 C，D 两点．则点 C 的坐标为 . 12. 如图，在平面直角坐标系中，点 A(-1，0)，B(0，3)，直线 BC 交坐标轴于 B， C 两点，且∠CBA=45° 则直线 BC 的解析式为 . 13. 如图，直线 y＝x＋4 与坐标轴交于点 A，B，点 C(－3，m)在直线 AB 上，在 y 轴上找一点 P，使 PA＋PC 的值最小，则这个最小值是 点 P 的坐标 为 ． 三．解答题. 14.如图①,在△ABC 中,AD 是三角形的高,且 AD=6 cm,E 是一个动点,由 B 向 C 移 动,其速度与时间的变化关系如图②, (1)求当 E 点在运动过程中△ABE 的面积 y 与运动时间 x 之间的关系式. (2)当点 E 移动 1.5 s 后停止,求此时△ABE 的面积. 15.如图,直线 y = 2x + 3 与 x 轴相交于点 A,与 y 轴相交于点 B. (1)求 A,B 两点的坐标. (2)过 B 点作直线 BP 与 x 轴的正半轴相交于点 P,且使 OP = 2OA,求△ABP 的面积. 16.如图,已知过点 B(1,0)的直线 l1 与直线 l2:y=2x+4 相交于点 P(-1,a) . (1)求直线 l1 的解析式; (2)求四边形 PAOC 的面积. 17. 如图,在平面直角坐标系中,过点 C(0,6)的直线 AC 与直线 OA 相交于点 A(4,2),动点 M 在线段 OA 和射线 AC 上运动,试解决下列问题: (1)求直线 AC 的表达式. (2)求△OAC 的面积. (3)是否存在点M,使△OMC的面积是△OAC 面积的 1 4 ?若存在,直接写出点M的坐标; 若不存在,请说明理由. 18.如图，A(0，4)，B(－4，0)，D(－2，0)，OE⊥AD 于点 F，交 AB 于点 E，BM⊥OB 交 OE 的延长线于点 M. (1)求直线 AB 和直线 AD 的解析式； (2)求点 M 的坐标； (3)求点 E，F的坐标． 19.如图，直线 1l 的解析表达式为：y=－3x＋3，且 1l 与 x 轴交于点 D，直线 2l 经过 点 A，B，直线 1l ， 2l 交于点 C． （1）求直线 2l 的解析表达式； （2）求△ADC 的面积； （3）在直线 2l 上存在一点 P，使得△ADP 的面积是△ADC 面积的 2 倍，请直接写 出点 P 的坐标． 20. 如图,已知函数 y=mx+ 4 3 的图象为直线 l1,函数 y=kx+b 的图象为直线 l2,直线 l1,l2 分别交 x 轴于点 B 和点 C(3,0),分别交 y 轴于点 D 和 E,l1 和 l2 相交于点 A(2,2). (1)填空:m=________; (2)求直线 l2 的解析式; (3)若点 M 是 x 轴上一点,连接 AM,当△ABM 的面积是△ACM 面积的 1 2 时,请求出符 合条件的点 M 的坐标; (4)若函数 y=ax+3 的图象是直线 l3,且 l1,l2,l3 不能围成三角形,直接写出 a 的值. 21. 如图,点 A 的坐标为(4,0).点 P 是直线 y=- 1 2 x+3 在第一象限内的点,过 P 作 PM⊥x 轴于点 M,O 是原点. (1)设点 P 的坐标为(x, y),试用它的纵坐标 y 表示△OPA 的面积 S. (2)S 与 y 是怎样的函数关系?它的自变量 y 的取值范围是什么? (3)如果用 P 的坐标表示△OPA 的面积 S,S 与 x 是怎样的函数关系?它的自变量的 取值范围是什么? (4)在直线 y=- 1 2 x+3 上求一点 Q,使△QOA 是以 OA 为底的等腰三角形.