2020年秋九年级数学上册 第3章 图形的相似 7页

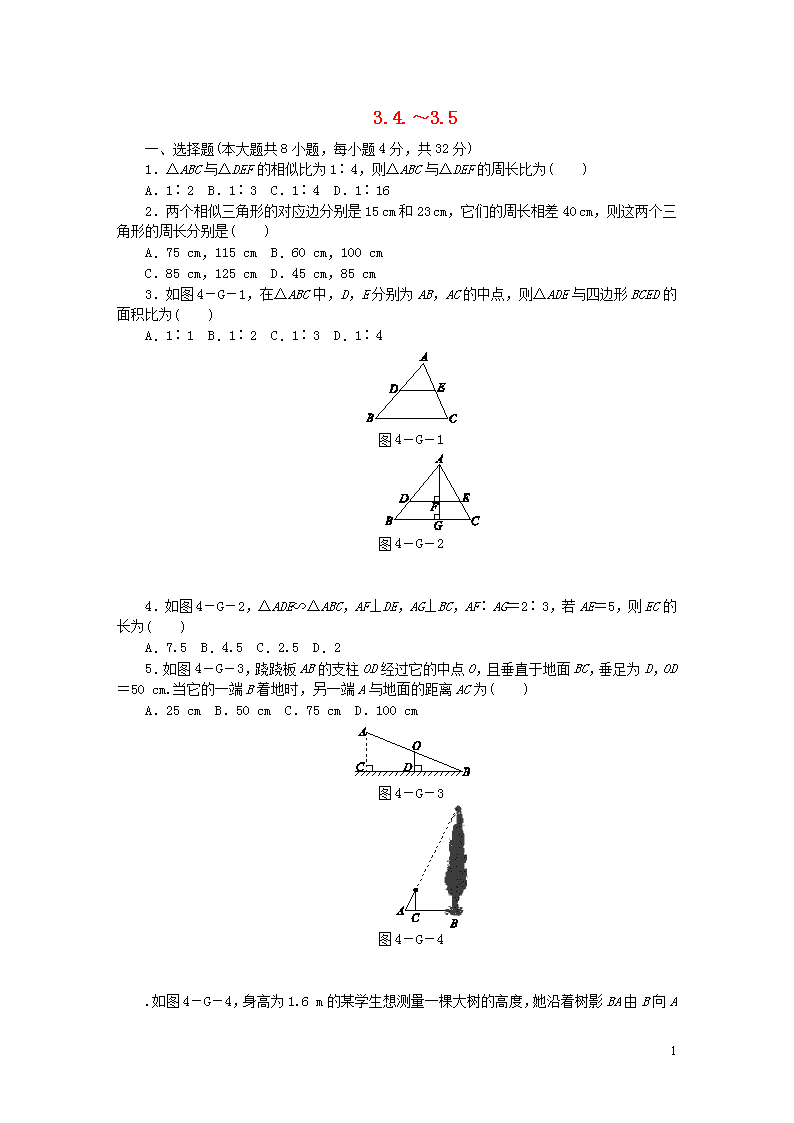
‎3.4.～3.5　‎ 一、选择题(本大题共8小题，每小题4分，共32分)‎ ‎1．△ABC与△DEF的相似比为1∶4，则△ABC与△DEF的周长比为(　　)‎ A．1∶2 B．1∶‎3 C．1∶4 D．1∶16‎ ‎2．两个相似三角形的对应边分别是‎15 cm和‎23 cm，它们的周长相差‎40 cm，则这两个三角形的周长分别是(　　)‎ A．‎75 cm，‎115 cm B．‎60 cm，‎‎100 cm C．‎85 cm，‎125 cm D．‎45 cm，‎‎85 cm ‎3．如图4－G－1，在△ABC中，D，E分别为AB，AC的中点，则△ADE与四边形BCED的面积比为(　　)‎ A．1∶1 B．1∶‎2 C．1∶3 D．1∶4‎ 图4－G－1‎ ‎　　　‎ 图4－G－2‎ ‎4．如图4－G－2，△ADE∽△ABC，AF⊥DE，AG⊥BC，AF∶AG＝2∶3，若AE＝5，则EC的长为(　　)‎ A．7.5 B．‎4.5 C．2.5 D．2‎ ‎5．如图4－G－3，跷跷板AB的支柱OD经过它的中点O，且垂直于地面BC，垂足为D，OD＝‎50 cm.当它的一端B着地时，另一端A与地面的距离AC为(　　)‎ A．‎25 cm B．‎50 cm C．‎75 cm D．‎‎100 cm 图4－G－3‎ ‎　　　‎ 图4－G－4‎ ‎.如图4－G－4，身高为‎1.6 m的某学生想测量一棵大树的高度，她沿着树影BA由B向A 7‎ 走去，当走到C点时，她的影子顶端正好与树的影子顶端重合，测得BC＝‎3.2 m，CA＝‎0.8 m，则树的高度为(　　)‎ A．‎4.8 m B．‎6.4 m C．‎8 m D．‎‎10 m ‎7．如图4－G－5，小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离)，在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(DE＝BC＝‎0.5米，A，B，C三点共线)，把一面镜子水平放置在平台上的点G处，测得CG＝‎15米，然后沿直线CG后退到点E处，这时恰好在镜子里看到凉亭的顶端A，测得EG＝‎3米，小明身高‎1.6米，则凉亭的高度AB约为(　　)‎ A．‎8.5米 B．‎9米 ‎ C．‎9.5米 D．‎‎10米 图4－G－5‎ ‎　　　‎ 图4－G－6‎ ‎8．如图4－G－6，在▱ABCD中，AC，BD相交于点O，E是OA的中点，连接BE并延长交AD于点F，已知S△AEF＝4，则下列结论：①＝；②S△BCE＝36；③S△ABE＝12；④△AEF∽△ACD.其中一定正确的是(　　)‎ A．①②③④ B．①④‎ C．②③④ D．①②③‎ 二、填空题(本大题共6小题，每小题4分，共24分)‎ ‎9．两个相似三角形对应中线的比为，则它们对应角平分线的比是________．‎ ‎10．如图4－G－7，在△ABC中，已知DE∥BC，＝，则△ADE与△ABC的面积之比为________．‎ 图4－G－7‎ ‎　　　‎ 图4－G－8‎ 7‎ ‎11．如图4－G－8所示，在Rt△ABC中，∠ACB＝90°，直线EF∥BC交AB于点E，交AC于点F.若S△AEF＝S四边形EBCF，则＝________.‎ 图4－G－9‎ ‎12．如图4－G－9，E是▱ABCD的边AD的中点，连接CE交BD于点F.如果S△DEF＝a，那么S△BCF＝________．‎ ‎13．如图4－G－10，阳光通过窗口AB照射到室内，在地面上留下‎4米宽的亮区DE，已知亮区DE到窗口下的墙角距离CE＝‎5米，窗口高AB＝‎2米，那么窗口底边离地面的高BC＝________米．‎ 图4－G－10‎ ‎　　　‎ 图4－G－11‎ ‎14．如图4－G－11，丁轩同学在晚上由路灯AC走向路灯BD，当他走到点P时，发现身后他影子的顶部刚好接触到路灯AC的底部，当他向前再步行‎20 m到达Q点时，发现身前他影子的顶部刚好接触到路灯BD的底部，已知丁轩同学的身高是‎1.5 m，两个路灯的高度都是‎9 m，则两路灯之间的距离是________m.‎ 三、解答题(本大题共4小题，共44分)‎ ‎15．(10分)已知两个相似三角形的一对对应边的长分别是‎35 cm和‎14 cm.‎ ‎(1)已知它们的周长相差‎60 cm，求这两个三角形的周长；‎ ‎(2)已知它们的面积相差‎588 cm2，求这两个三角形的面积．‎ ‎16．(10分)如图4－G－12，有一块三角形的土地，它的一条边BC＝‎100米，BC边上的高AH＝‎80米．某单位要沿着边BC建一座底面是矩形DEFG的大楼，D，G分别在边AB，AC上．若大楼的宽是‎40米(即DE＝‎40米)，求这个矩形的面积．‎ 7‎ 图4－G－12‎ ‎17．(12分)如图4－G－13所示，在离某建筑物‎4 m处有一棵树AB，在某一时刻，‎1.2 m长的竹竿A′B′垂直于地面，影长为‎2 m，此时，树的影子有一部分落在地面上，还有一部分影子落在建筑物的墙上，墙上的影高CD为‎2 m，那么这棵树的高度为多少米？‎ 图4－G－13‎ ‎18．(12分)已知△ABC∽△A′B′C′，＝，AB边上的中线CD＝‎4 cm，△ABC的周长为‎20 cm，△A′B′C′的面积为‎64 cm2.‎ 求：(1)A′B′边上的中线C′D′的长；‎ ‎(2)△A′B′C′的周长；‎ ‎(3)△ABC的面积．‎ 详解详析 ‎1．C　[解析] ∵△ABC与△DEF相似，且相似比为1∶4，∴△ABC与△DEF的周长比＝相似比＝1∶4，故选择C.‎ ‎2．A　[解析]‎ 7‎ ‎ 根据题意知两个三角形的相似比是15∶23，则周长比就是15∶23，它们的周长相差8份，所以每份的周长是40÷8＝5(cm)，所以两个三角形的周长分别为5×15＝75(cm)，5×23＝115(cm)．故选A.‎ ‎3．C　[解析] ∵D，E分别为△ABC的边AB，AC的中点，∴DE是△ABC的中位线，‎ ‎∴DE∥BC，DE＝BC，∴△ADE∽△ABC，‎ ‎∴△ADE的面积∶△ABC的面积＝()2＝1∶4，‎ ‎∴△ADE的面积∶四边形BCED的面积＝1∶3.故选C.‎ ‎4．C　[解析] ∵△ADE∽△ABC，AF⊥DE，AG⊥BC，∴＝＝，∴＝，解得AC＝7.5，∴EC＝7.5－5＝2.5.‎ ‎5．D ‎6．C　[解析] 因为人和树均垂直于地面，所以和光线构成的两个直角三角形相似，设树高为x m，则＝，即＝，∴x＝8，故选C.‎ ‎7．A　[解析] 由题意得∠AGC＝∠FGE.又∵∠ACG＝∠FEG＝90°，∴△ACG∽△FEG，∴＝，∴＝，解得AC＝8(米)，‎ ‎∴AB＝AC＋BC＝8＋0.5＝8.5(米)．故选A.‎ ‎8．D　[解析] 在▱ABCD中，AO＝AC.‎ ‎∵E是OA的中点，∴AE＝CE.‎ ‎∵AD∥BC，∴△AFE∽△CBE，‎ ‎∴＝＝.‎ ‎∵AD＝BC，∴AF＝AD，∴＝.故①正确．‎ ‎∵S△AEF＝4，＝()2＝，∴S△BCE＝36.‎ 故②正确．∵＝＝，∴＝，∴S△ABE＝12.故③正确．∵BF不平行于CD，∴△AEF与△ADC只有一个角相等，∴△AEF与△ACD不一定相似，故④错误．故选D.‎ ‎9. ‎10．4∶25　[解析] ∵DE∥BC，‎ ‎∴△ADE∽△ABC.∵＝，∴＝，‎ ‎∴S△ADE∶S△ABC＝4∶25.‎ ‎11. ‎12．‎4a　[解析] ∵四边形ABCD是平行四边形，∴AD∥BC，∴△EFD∽△CFB.‎ ‎∵E是边AD的中点，∴DE＝AD＝BC，∴S△DEF∶S△BCF＝1∶4.‎ 7‎ ‎∵S△DEF＝a，∴S△BCF＝‎4a.‎ ‎13．2.5　[解析] ∵AD∥BE，∴△BCE∽△ACD，∴＝，CD＝CE＋ED＝4＋5＝9，AC＝BC＋AB＝BC＋2，‎ ‎∴＝，解得BC＝2.5.‎ ‎14．30　[解析] ∵MP∥BD，∴＝.同理，＝.∵AC＝BD，∴AP＝BQ.设AP＝BQ＝x，则AB＝2x＋20.∵NQ∥AC，‎ ‎∴△BQN∽△BAC，∴＝，即＝，解得x＝5.则两路灯之间的距离是2×5＋20＝30(m)．‎ ‎15．解：(1)∵相似三角形的一对对应边的长分别是‎35 cm和‎14 cm，‎ ‎∴这两个三角形的相似比为5∶2，‎ ‎∴这两个三角形的周长比为5∶2.‎ 设较大的三角形的周长为5x cm，则较小的三角形的周长为2x cm，‎ ‎∵它们的周长相差‎60 cm，‎ ‎∴3x＝60，解得x＝20，‎ ‎∴5x＝5×20＝100，2x＝2×20＝40，‎ ‎∴较大的三角形的周长为‎100 cm，较小的三角形的周长为‎40 cm.‎ ‎(2)∵这两个三角形的相似比为5∶2，‎ ‎∴这两个三角形的面积比为25∶4.‎ 设较大的三角形的面积为25y cm2，则较小的三角形的面积为4y cm2，‎ ‎∵它们的面积相差‎588 cm2，‎ ‎∴(25－4)y＝588，解得y＝28，‎ ‎∴25y＝25×28＝700，4y＝4×28＝112，‎ ‎∴较大的三角形的面积为‎700 cm2，较小的三角形的面积为‎112 cm2.‎ ‎16．解：设AH交DG于点M.由已知得DG∥BC，‎ ‎∴△ADG∽△ABC.‎ ‎∵AH⊥BC，‎ ‎∴AM⊥DG，AM＝AH－MH＝80－40＝40(米)．‎ ‎∵＝，∴DG＝＝‎50米，‎ ‎∴S矩形DEFG＝DE·DG＝40×50＝2000(米2)．‎ 答：这个矩形的面积为2000平方米．‎ ‎17．过点C作CE∥AD交AB于点E，‎ 则CD＝AE＝2 m，△B′BA′∽△BCE，‎ ‎∴＝，即＝，‎ 解得BE＝2.4(m)．∴AB＝2.4＋2＝4.4(m)．‎ 答：这棵树的高度为4.4 m.‎ 7‎ ‎18．解：(1)∵△ABC∽△A′B′C′，＝，AB边上的中线CD＝‎4 cm，‎ ‎∴＝，∴C′D′＝4×2＝8(cm)，‎ ‎∴A′B′边上的中线C′D′的长为‎8 cm.‎ ‎(2)∵△ABC∽△A′B′C′，＝，△ABC的周长为‎20 cm，‎ ‎∴△A′B′C′的周长＝20×2＝40(cm)，‎ 即△A′B′C′的周长为40 cm.‎ ‎(3)∵△ABC∽△A′B′C′，＝，△A′B′C′的面积是‎64 cm2，∴＝()2＝，‎ ‎∴S△ABC＝64÷4＝16(cm2)，‎ 即△ABC的面积是16 cm2.‎ 7‎