九年级上册数学周周测第二十二章 二次函数周周测6（整章） 人教版 5页

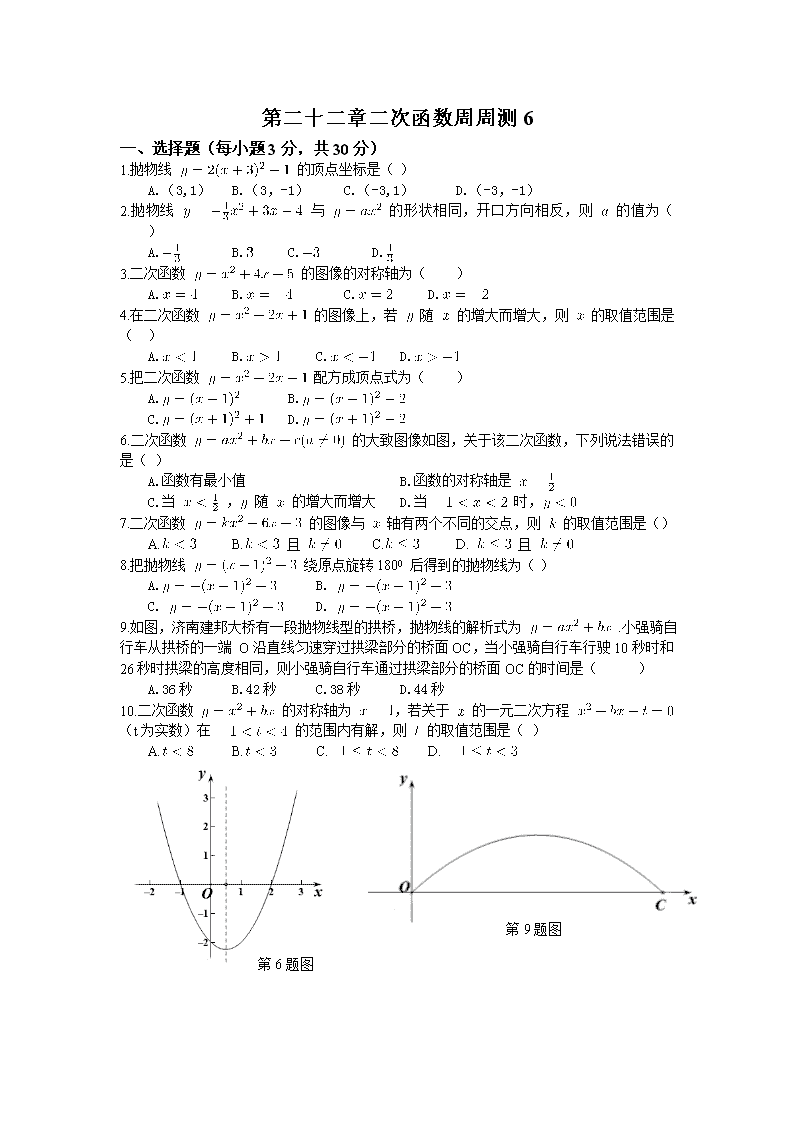
第二十二章二次函数周周测6‎ 一、选择题（每小题3分，共30分）‎ ‎1.抛物线 的顶点坐标是（ ）‎ A.（3,1） B.（3，-1） C.（-3,1） D.（-3，-1）‎ ‎2.抛物线 与 的形状相同，开口方向相反，则 的值为（ ）‎ A. B. C. D.‎ ‎3.二次函数 的图像的对称轴为（ ）‎ A. B. C. D.‎ ‎4.在二次函数 的图像上，若 随 的增大而增大，则 的取值范围是（ ）‎ A. B. C. D.‎ ‎5.把二次函数 配方成顶点式为（ ）‎ A. B. ‎ C. D.‎ ‎6.二次函数 的大致图像如图，关于该二次函数，下列说法错误的是（ ）‎ A.函数有最小值 B.函数的对称轴是 ‎ C.当 ， 随 的增大而增大 D.当 时，‎ ‎7.二次函数 的图像与 轴有两个不同的交点，则 的取值范围是（）‎ A. B. 且 C. D. 且 ‎ ‎8.把抛物线 绕原点旋转1800 后得到的抛物线为（ ）‎ A. B. ‎ C. D. ‎ ‎9.如图，济南建邦大桥有一段抛物线型的拱桥，抛物线的解析式为 .小强骑自行车从拱桥的一端 O沿直线匀速穿过拱梁部分的桥面OC，当小强骑自行车行驶10秒时和26秒时拱梁的高度相同，则小强骑自行车通过拱梁部分的桥面OC的时间是（ ）‎ A.36秒 B.42秒 C.38秒 D.44秒 ‎10.二次函数 的对称轴为 ，若关于 的一元二次方程 （t为实数）在 的范围内有解，则 的取值范围是（ ）‎ 第6题图 第9题图 A. B. C. D. ‎ ‎ ‎ 二、填空题（每小题3分，共18分）‎ ‎11.抛物线 有 点（填“高”或“低”），其坐标是 .‎ ‎12.若抛物线 与 轴分别交于A，B两点，A，B两点的坐标分别是 ‎ ‎13.已知抛物线 的对称轴是 。则 的值为 ‎ ‎14.若抛物线 的顶点与原点的距离为5，则 的值为 ‎ ‎15.在距离地面2m的高的某处把一物体以初速度 （m/s）竖直向上抛出，在不计空气阻力的情况下，其上升高度 （m）与抛出时间 （s）满足： （其中 是常数，通常取10 m/s2）.若 ， 则该物体在运动过程中最高点距地面 m.‎ ‎16.当 ，函数 的图像记为G，将图像G在 轴上方的部分沿 轴翻折，图像G的其余部分保持不变，得到一个新图像M，若直线 与图像M有且只有两个公共点，则 的取值范围是 .‎ 三、解答题（共8题，共72分）‎ ‎17.（本题8分）已知二次函数 .‎ ‎（1）求它的开口方向、对称轴和顶点坐标；‎ ‎（2）判断点 A（-1,6）是否在此二次函数的图像上？‎ ‎18.（本题8分）已知抛物线经过点（2,3），且顶点坐标为（1,1），求这条抛物线的解析式.‎ ‎19.（本题8分）如图，已知抛物线 经过 A（-1,0），B（3,0） 两点.‎ ‎（1）求抛物线的解析式和顶点坐标；‎ ‎（2）当 ，求 的取值范围。‎ ‎20.（本题8分）二次函数 的图像如图所示，根据图像解决下列问题：‎ ‎（1）写出方程 的两个根；‎ ‎（2）写出不等式 的解集；‎ ‎（3）写出 随 的增大而减小的自变量 的取值范围；‎ ‎（4）若方程 有两个不相等的实数根，求 的取值范围。‎ ‎21.（本题8分）手工课上，小明准备做一个形状菱形ABCD的风筝，这个菱形的两条对角线长度之和恰好为60cm，菱形的面积S（单位：cm2）随其中一条对角线BD的长（单位：cm）的变化而变化.‎ ‎（1）请直接写出S与 之间的函数关系式；‎ ‎（2）当 是多少时，菱形风筝的面积S最大？最大面积是多少？‎ ‎22.（本题10分）已知二次函数 .‎ ‎（1）如果二次函数的图像与 轴有两个交点，求 的取值范围；‎ ‎（2）如图，二次函数的图像过点A（3,0），与 轴交于点B，直线AB与这个二次函数图像的对称轴交于点P，求 的值。‎ ‎23.（本题10分）在“母亲节”前夕，我市某校学生积极参与“关爱贫困母亲”的活动，他们购进一批单价为20元的“孝文化衫”在课余时间进行义卖，并将所得利润捐给贫困母亲.经试验发现，若每件按24元的价格销售时，每天能卖出36件；若每件按29元的价格销售时，每天能卖出21件.假定每天销售件数 （件）与销售价格 （元/件）满足一个以 为自变量的一次函数.‎ ‎（1）求 与 满足的函数解析式；‎ ‎（2）设每天获得的利润为 W（元），‎ ‎①求W与 满足的函数解析式;‎ ‎②在不积压且不考虑其他因素的情况下，销售价格定位多少元时，才能使每天获得的利润最大？‎ ‎24.（本题12分）如图1，抛物线 与 轴交于A，B两点，与 轴交于C点，直线 与抛物线交于D，E，与直线BC交于P.‎ ‎（1）求点P的坐标；‎ ‎（2）求PD·EP的值；‎ ‎（3）如图2，直线 交抛物线于F，G，且△FCG的外心在FG上，求证： 为常数.‎