2020年秋九年级数学上册 第3章 图形的相似 3 8页

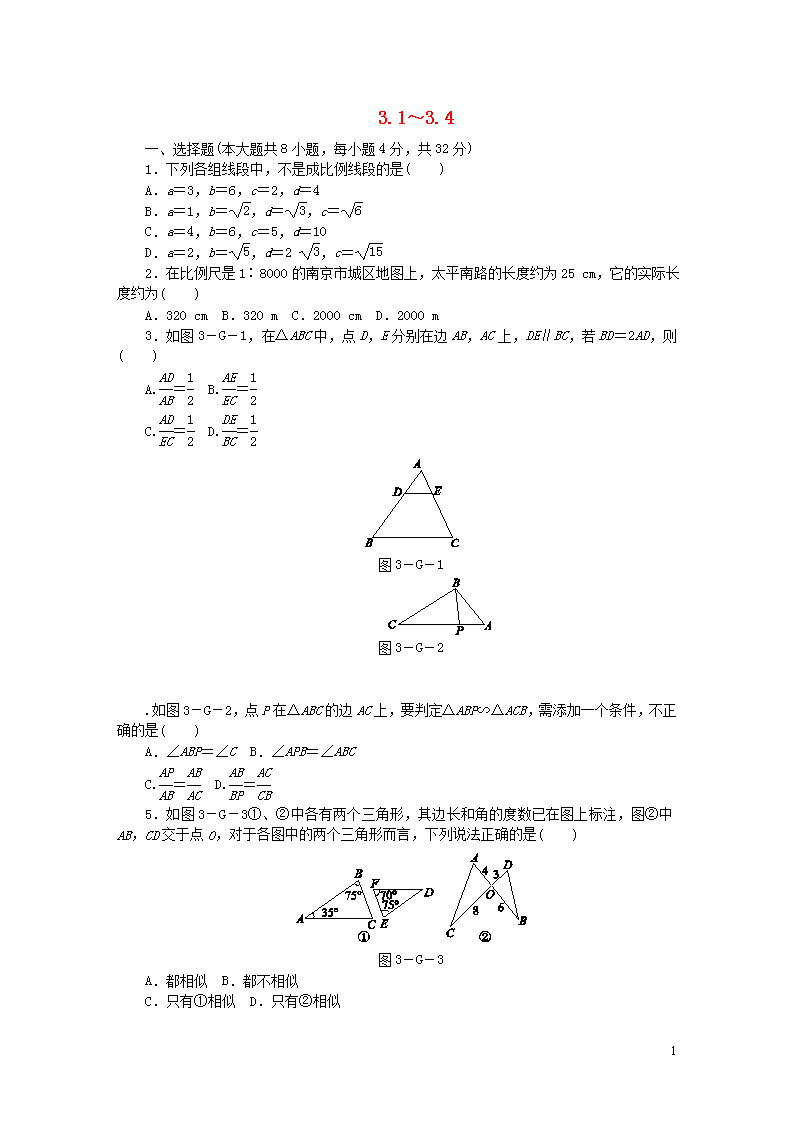
‎3.1～3.4　　　　　　　　　　　　‎ 一、选择题(本大题共8小题，每小题4分，共32分)‎ ‎1．下列各组线段中，不是成比例线段的是(　　)‎ A．a＝3，b＝6，c＝2，d＝4‎ B．a＝1，b＝，d＝，c＝ C．a＝4，b＝6，c＝5，d＝10‎ D．a＝2，b＝，d＝2 ，c＝ ‎2．在比例尺是1∶8000的南京市城区地图上，太平南路的长度约为‎25 cm，它的实际长度约为(　　)‎ A．‎320 cm　B．‎320 m　C．‎2000 cm　D．‎‎2000 m ‎3．如图3－G－1，在△ABC中，点D，E分别在边AB，AC上，DE∥BC，若BD＝2AD，则(　　)‎ A.＝ B.＝ C.＝ D.＝ 图3－G－1‎ ‎　　　　‎ 图3－G－2‎ ‎.如图3－G－2，点P在△ABC的边AC上，要判定△ABP∽△ACB，需添加一个条件，不正确的是(　　)‎ A．∠ABP＝∠C B．∠APB＝∠ABC C.＝ D.＝ ‎5．如图3－G－3①、②中各有两个三角形，其边长和角的度数已在图上标注，图②中AB，CD交于点O，对于各图中的两个三角形而言，下列说法正确的是(　　)‎ 图3－G－3‎ A．都相似 B．都不相似 C．只有①相似 D．只有②相似 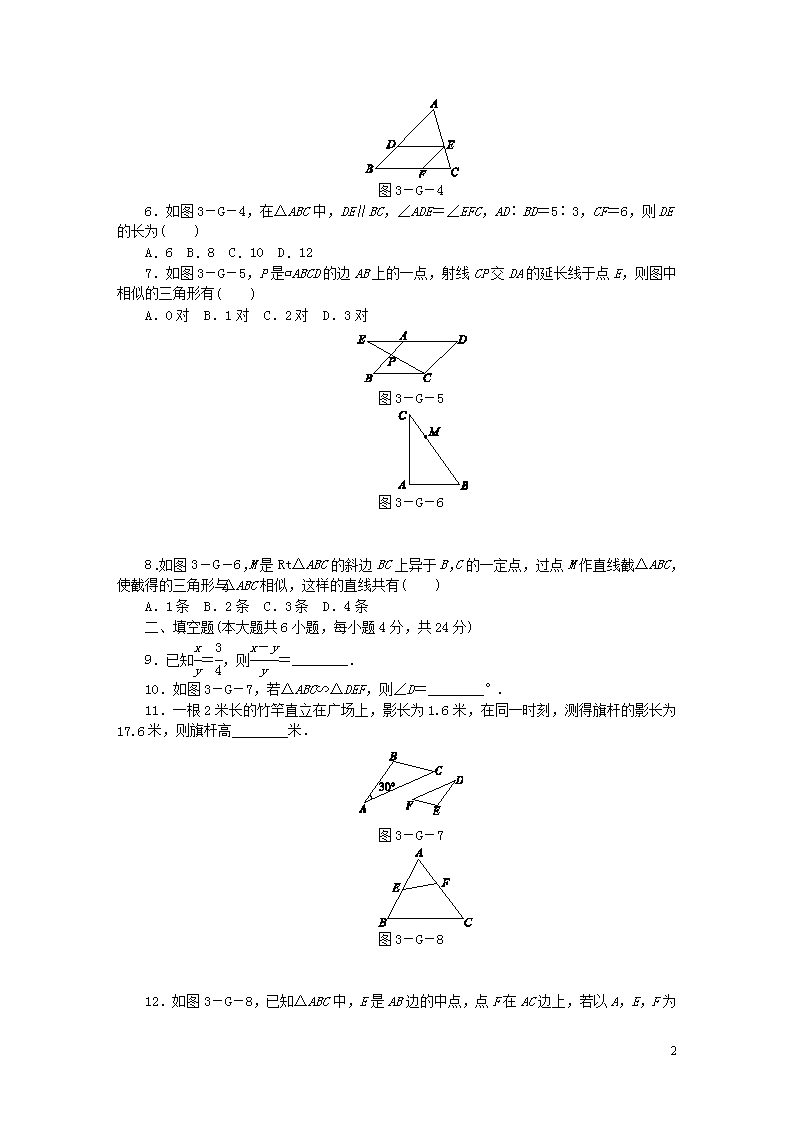8‎ 图3－G－4‎ ‎6．如图3－G－4，在△ABC中，DE∥BC，∠ADE＝∠EFC，AD∶BD＝5∶3，CF＝6，则DE的长为(　　)‎ A．6 B．‎8 C．10 D．12‎ ‎7．如图3－G－5，P是▱ABCD的边AB上的一点，射线CP交DA的延长线于点E，则图中相似的三角形有(　　)‎ A．0对 B．1对 C．2对 D．3对 图3－G－5‎ ‎　　　‎ 图3－G－6‎ ‎8．如图3－G－6，M是Rt△ABC的斜边BC上异于B，C的一定点，过点M作直线截△ABC，使截得的三角形与△ABC相似，这样的直线共有(　　)‎ A．1条 B．2条 C．3条 D．4条 二、填空题(本大题共6小题，每小题4分，共24分)‎ ‎9．已知＝，则＝________．‎ ‎10．如图3－G－7，若△ABC∽△DEF，则∠D＝________°.‎ ‎11．一根‎2米长的竹竿直立在广场上，影长为‎1.6米，在同一时刻，测得旗杆的影长为‎17.6米，则旗杆高________米．‎ 图3－G－7‎ ‎　　‎ 图3－G－8‎ ‎12．如图3－G－8，已知△ABC中，E是AB边的中点，点F在AC边上，若以A，E，F 8‎ 为顶点的三角形与△ABC相似，则需要增加的一个条件是________．(写出一个即可)‎ ‎13．如图3－G－9，E为▱ABCD的边AB延长线上的一点，且BE∶AB＝2∶3，连接DE交BC于点F，则CF∶AD＝________．‎ 图3－G－9‎ ‎　　　‎ 图3－G－10‎ ‎14．如图3－G－10，△ABC中，AC＝6，AB＝4，点D，A在直线BC同侧，且∠ACD＝∠ABC，CD＝2，点E是线段BC延长线上的动点，当△DCE和△ABC相似时，线段CE的长为________．‎ 三、解答题(本大题共4小题，共44分)‎ ‎15．(10分)如图3－G－11，在▱ABCD中，M，N为BD的三等分点，连接CM并延长交AB于点E，连接EN并延长交CD于点F，求DF∶AB的值．‎ 图3－G－11‎ ‎16．(10分)如图3－G－12，＝＝.‎ 8‎ 求证：∠BAD＝∠CAE.‎ 图3－G－12‎ ‎17．(12分)如图3－G－13，在△ABC中，AB＝AC，点E在边BC上移动(点E不与点B，C重合)，满足∠DEF＝∠B，且点D，F分别在边AB，AC上．‎ ‎(1)求证：△BDE∽△CEF；‎ ‎(2)当点E移动到BC的中点时，求证：FE平分∠DFC.‎ 图3－G－13‎ ‎18．(12分)如图3－G－14，正方形ABCD的边长为1，AB边上有一动点P，连接PD，线段PD绕点P顺时针旋转90°后，得到线段PE，且PE交BC于点F，连接DF，过点E作EQ⊥AB交AB的延长线于点Q.‎ ‎(1)求线段PQ的长；‎ ‎(2)当点P在何处时，△PFD∽△BFP？并说明理由．‎ 8‎ 图3－G－14‎ 8‎ ‎　　　详解详析 ‎1．C　2.D ‎3．B　[解析] ∵DE∥BC，∴△ADE∽△ABC.∵BD＝2AD，∴＝＝＝，则＝.故选B.‎ ‎4．D　[解析] 选项A，B，C中结合条件∠A＝∠A均可判定△ABP∽△ACB，只有选项D无法得到△ABP∽△ACB，故选D.‎ ‎5．A　[解析] 图①中，∵∠A＝35°，∠B＝75°，‎ ‎∴∠C＝180°－∠A－∠B＝70°.‎ ‎∵∠E＝75°，∠F＝70°，∴∠B＝∠E，∠C＝∠F，∴△ABC∽△DEF；‎ 图②中，∵OA＝4，OD＝3，OC＝8，OB＝6，‎ ‎∴＝.‎ 又∵∠AOC＝∠DOB，∴△AOC∽△DOB.‎ ‎6．C　[解析] ∵DE∥BC，∴∠ADE＝∠B.∵∠ADE＝∠EFC，∴∠B＝∠EFC，∴BD∥EF.又∵DE∥BF，∴四边形BDEF为平行四边形，∴DE＝BF.∵DE∥BC，∴△ADE∽△ABC，∴＝＝＝，∴BC＝DE，∴CF＝BC－BF＝DE＝6，∴DE＝10.故选C.‎ ‎7．D　[解析] △EAP∽△EDC，△EAP∽△CBP，∴△EDC∽△CBP，∴共有3对相似三角形．故选D.‎ ‎8． C　[解析] 如图，分别过点M作△ABC三边的垂线l1，l2，l3，易证此时分别形成的三角形均与原三角形相似，所以共有3条．‎ ‎9．－　10.30‎ ‎11．22　[解析] 设旗杆的高为x米，∵在同一时刻物高与影长成正比，∴＝，∴x＝22.‎ ‎12．答案不唯一，如AF＝AC或∠AFE＝∠ABC等 ‎13.　[解析] 由题意可知CD∥AE，CD＝AB，∴△CDF∽△BEF，∴＝.‎ ‎∵＝＝，∴＝，∴＝.‎ ‎∵AD＝BC，∴＝＝.‎ ‎14 或3　[解析] ∵∠ACD＋∠DCE＝∠B＋∠A，∠ACD＝∠B，∴∠DCE＝∠A，‎ ‎∴∠A与∠DCE是对应角，‎ 8‎ ‎∴△DCE和△ABC相似有两种情况：‎ ‎(1)当△BAC∽△ECD时，＝，‎ ‎∴＝，∴CE＝；‎ ‎(2)当△BAC∽△DCE时，＝，‎ ‎∴＝，∴CE＝3.‎ 综上所述，CE的长为或3.‎ ‎15．解：由题意可得DN＝NM＝MB，△DFN∽△BEN，△DMC∽△BME，‎ ‎∴DF∶BE＝DN∶NB＝1∶2，BE∶DC＝BM∶MD＝1∶2.‎ 又∵AB＝DC，‎ ‎∴DF∶AB＝1∶4＝.‎ ‎16．[解析] 将已有的比例线段归属在两个三角形中观察，以寻找相似三角形，利用相似三角形的对应角相等证明．‎ 证明： ∵＝＝，‎ ‎∴△ABC∽△ADE，‎ ‎∴∠BAC＝∠DAE，‎ ‎∴∠BAC－∠DAC＝∠DAE－∠DAC，‎ 即∠BAD＝∠CAE.‎ ‎17．证明：(1)∵AB＝AC，‎ ‎∴∠B＝∠C.‎ ‎∵∠BDE＝180°－∠B－∠DEB，‎ ‎∠CEF＝180°－∠DEF－∠DEB，‎ 又∵∠DEF＝∠B，‎ ‎∴∠BDE＝∠CEF，‎ ‎∴△BDE∽△CEF.‎ ‎(2)∵△BDE∽△CEF，∴＝.‎ ‎∵E是BC的中点，∴BE＝CE，‎ ‎∴＝，∴＝.‎ 又∵∠DEF＝∠B＝∠C，‎ ‎∴△DEF∽△ECF，‎ ‎∴∠DFE＝∠CFE，‎ ‎∴FE平分∠DFC.‎ ‎18． (1)根据题意，得PD＝PE，∠DPE＝90°，‎ ‎∴∠APD＋∠QPE＝90°.‎ ‎∵四边形ABCD是正方形，∴∠A＝90°，‎ ‎∴∠ADP＋∠APD＝90°，‎ 8‎ ‎∴∠ADP＝∠QPE.‎ ‎∵EQ⊥AB，∴∠Q＝90°＝∠A.‎ 在△ADP和△QPE中，‎ ‎∴△ADP≌△QPE(AAS)，‎ ‎∴PQ＝AD＝1.‎ ‎(2)假设△PFD∽△BFP，则有＝.‎ ‎∵∠ADP＝∠BPF，∠FBP＝∠A，‎ ‎∴△DAP∽△PBF，‎ ‎∴＝，∴＝.‎ ‎∴AP＝PB，∴AP＝AB＝.‎ 即当P为AB的中点时，△PFD∽△BFP.‎ 8‎