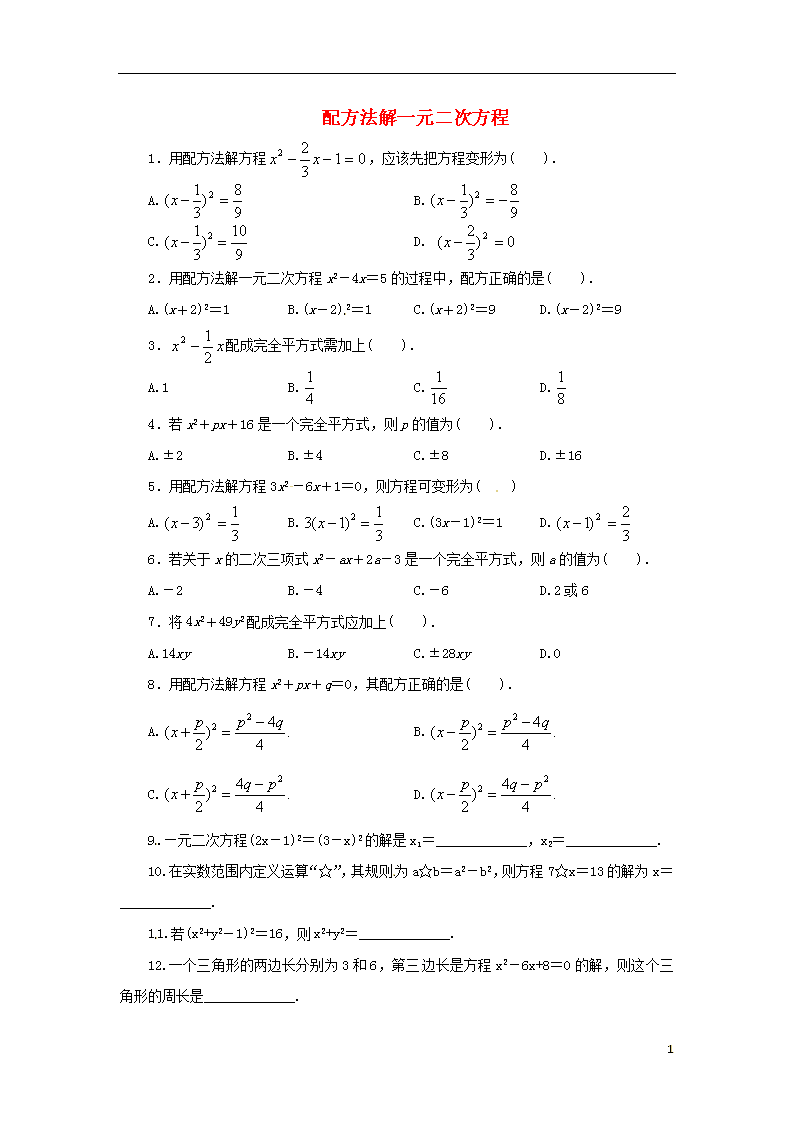2019九年级数学上册 第22章 22配方法解一元二次方程 4页

配方法解一元二次方程 ‎1．用配方法解方程，应该先把方程变形为( )．‎ A. B.‎ C. D. ‎ ‎2．用配方法解一元二次方程x2－4x＝5的过程中，配方正确的是( )．‎ A.(x＋2)2＝1 B.(x－2)2＝‎1 ‎C.(x＋2)2＝9 D.(x－2)2＝9‎ ‎3．配成完全平方式需加上( )．‎ A.1 B. C. D.‎ ‎4．若x2＋px＋16是一个完全平方式，则p的值为( )．‎ A.±2 B.±‎4 ‎C.±8 D.±16‎ ‎5．用配方法解方程3x2－6x＋1＝0，则方程可变形为( )‎ A. B. C.(3x－1)2＝1 D.‎ ‎6．若关于x的二次三项式x2－ax＋‎2a－3是一个完全平方式，则a的值为( )．‎ A.－2 B.－‎4 ‎C.－6 D.2或6‎ ‎7．将4x2＋49y2配成完全平方式应加上( )．‎ A.14xy B.－14xy C.±28xy D.0‎ ‎8．用配方法解方程x2＋px＋q＝0，其配方正确的是( )．‎ A. B.‎ C. D.‎ ‎9.—元二次方程(2x－1)2＝(3－x)2的解是x1＝_____________，x2＝_____________.‎ ‎10.在实数范围内定义运算“☆”，其规则为a☆b＝a2－b2，则方程7☆x＝13的解为x＝_____________.‎ ‎11.若(x2+y2－1)2＝16，则x2+y2＝_____________.‎ ‎12.一个三角形的两边长分别为3和6，第三边长是方程x2－6x+8＝0的解，则这个三角形的周长是_____________.‎ 4‎ ‎13.已知实数x满足4x2+4x+1＝0，则代数式的值为_____________.‎ ‎14.如果一个三角形的三边长均满足方程x2－10x+25＝0，那么此三角形的面积是_____________.‎ ‎15.小明设计了一个魔术盒，当任意实数对(a，b)进入其中时，会得到一个新的实数a2－2b+3.若将实数对(x，－2x)放入其中得到－1，则x＝_____________.‎ ‎16.用配方法解下列方程.‎ ‎（1）x2+2mx－n2＝0；‎ ‎（2）4x2－7x－2＝0.‎ ‎17.阅读材料：用配方法求最值.‎ 已知x，y为非负实数，‎ ‎∵，‎ ‎∴，当且仅当“x＝y”时，等号成立.‎ 示例：当x>0时，求的最小值.‎ 解：，当，‎ 即x＝1时，y的最小值为6.‎ ‎（1）尝试：当x>0时，求的最小值.‎ ‎（2）问题解决：随着人们生活水平的快速提高，小轿车已成为越来越多家庭的交通工具，假设某种小轿车的购车费用为10万元，每年应缴保险费等各类费用共计0.4万元，n年的保养、维护费用总和为万元.问：这种小轿车使用多少年报废最合算（即：使用多少年的年平均费用最少，年平均费用）？最少年平均费用为多少万元？‎ 4‎ 参考答案 ‎1．C． 2．D． 3．C． 4．C．‎ ‎5．D． 6．D． 7．C． 8．A．‎ ‎9. －2 解析 方程两边开平方得2x－1＝±(3－x)，‎ 即：当2x－1＝3－x时，；当2x－1＝－(3－x)时，x＝－2.‎ ‎10.±6 解析 因为规则为a☆b＝a2－b2，‎ 所以由方程7☆x＝13可得49－x2＝13，整理得x2＝36，‎ 所以x＝±6.‎ ‎11.5 解析 直接开平方得x2+y2－1＝±4，∴x2+y2＝5或－3.‎ 又∵x2+y2≥0，∴x2+y2＝5.‎ ‎12.13 解析 x2－6x+8＝0配方得(x－3)2＝1，解得x1＝2，x2＝4.当x＝2时，2+3<6，此时不能组成三角形，所以舍去；当x＝4时，三角形的周长为3+4+6＝13.‎ ‎13.－2 解析 由4x2+4x+1＝0，得(2x+1)2＝0，所以2x＝－1，‎ 故.‎ ‎14. 解析 由x2－10+25＝0，得(x－5)2＝0，‎ ‎∴x1＝x2＝5.‎ ‎∵三角形的三边长均满足方程x2－10x+25＝0，‎ ‎∴此三角形是以5为边长的等边三角形，可求得三角形一边上的高为，‎ ‎∴三角形的面积.‎ ‎15.－2 解析 由题意得x2－2x(－2x)+3＝－1，整理得x2+4x+4＝0，解得x1＝x2＝－2.‎ ‎16.解：（1）移项，得x2+2mx＝n2，‎ 配方，得x2+2mx+m2＝n2+m2，‎ 即(x+m)2＝m2+n2，所以，‎ 所以，.‎ ‎（2）方程两边都除以4，得，‎ 4‎ 移项，得，‎ 配方，得，‎ 即，‎ 开平方，得，‎ 即或.‎ 所以x1＝2，.‎ 注意：利用配方法解一元二次方程应注意以下两点：①当方程的二次项系数不是1的时候，一定要先将二次项系数化为1，再进行配方；②在二次项系数是1的前提下，将常数项移到方程的右边，方程两边同时加上一次项系数一半的平方.‎ ‎17.思路建立 （1）要求的最小值，题中给出配方法的应用示例，根据示例得，然后应用配方法，求出当x>0时，的最小值即可.‎ ‎（2）要求最少年平均费用，首先根据题意，求出年平均费用，然后求出这种小轿车使用多少年报废最合算，以及最少年平均费用为多少万元即可.‎ 解：（1），‎ ‎∴当，即x＝1时，y的最小值为3.‎ ‎（2）年平均费用，‎ ‎∴当，即n＝10时，报废最合算，最少年平均费用为2.5万元.‎ 4‎