中考数学专题复习练习：圆的综合题 4页

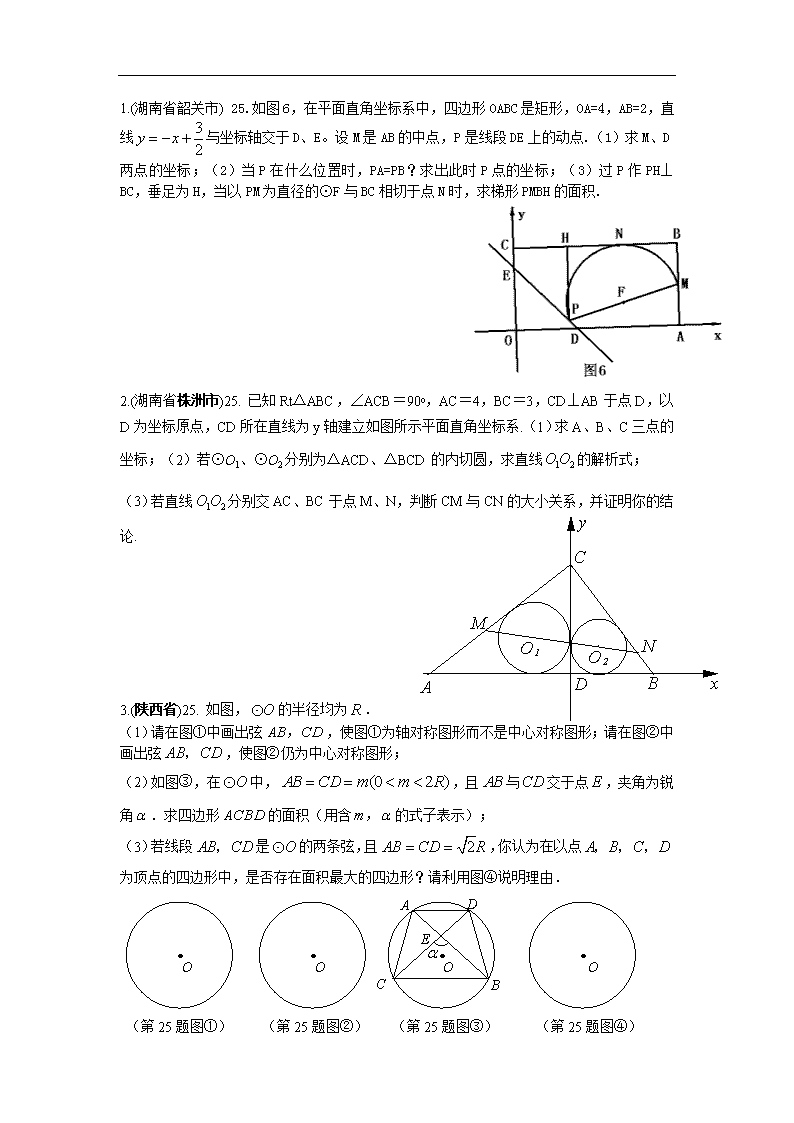
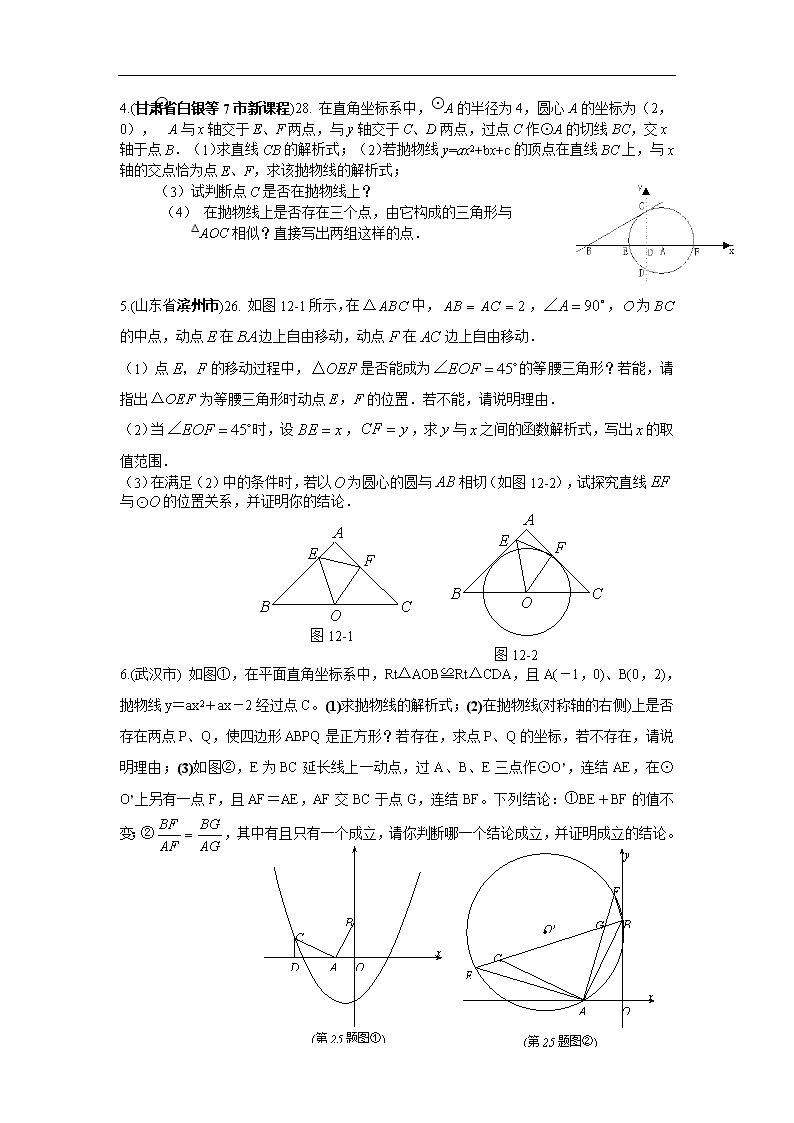
1.(湖南省韶关市) 25.如图 6，在平面直角坐标系中，四边形 OABC 是矩形，OA=4，AB=2，直 线 与坐标轴交于 D、E。设 M 是 AB 的中点，P 是线段 DE 上的动点.（1）求 M、D 两点的坐标；（2）当 P 在什么位置时，PA=PB？求出此时 P 点的坐标；（3）过 P 作 PH⊥ BC，垂足为 H，当以 PM 为直径的⊙F 与 BC 相切于点 N 时，求梯形 PMBH 的面积. 2.(湖南省株洲市)25. 已知 Rt△ABC，∠ACB＝90o，AC＝4，BC＝3，CD⊥AB 于点 D，以 D 为坐标原点，CD 所在直线为 y 轴建立如图所示平面直角坐标系.（1）求 A、B、C 三点的 坐标；（2）若⊙O1、⊙O2 分别为△ACD、△BCD 的内切圆，求直线 的解析式； （3）若直线 分别交 AC、BC 于点 M、N，判断 CM 与 CN 的大小关系，并证明你的结 论. 3.(陕西省)25. 如图， 的半径均为 ． （1）请在图①中画出弦 ，使图①为轴对称图形而不是中心对称图形；请在图②中 画出弦 ，使图②仍为中心对称图形； （2）如图③，在 中， ，且 与 交于点 ，夹角为锐 角 ．求四边形 的面积（用含 的式子表示）； （3）若线段 是 的两条弦，且 ，你认为在以点 为顶点的四边形中，是否存在面积最大的四边形？请利用图④说明理由． 3 2y x= − + 1 2O O 1 2O O O R AB CD， AB CD， O (0 2 )AB CD m m R= = < < AB CD E α ACBD m α， AB CD， O 2AB CD R= = A B C D， ， ， xA B C M N D O 1 O 2 y O O O A D E C B O （第 25 题图①） （第 25 题图②） （第 25 题图③） （第 25 题图④） α 4.(甘肃省白银等 7 市新课程)28. 在直角坐标系中，⊙A 的半径为 4，圆心 A 的坐标为（2， 0），⊙A 与 x 轴交于 E、F 两点，与 y 轴交于 C、D 两点，过点 C 作⊙A 的切线 BC，交 x 轴于点 B．（1）求直线 CB 的解析式；（2）若抛物线 y=ax2+bx+c 的顶点在直线 BC 上，与 x 轴的交点恰为点 E、F，求该抛物线的解析式； （3）试判断点 C 是否在抛物线上？ （4） 在抛物线上是否存在三个点，由它构成的三角形与 △AOC 相似？直接写出两组这样的点． 5.(山东省滨州市)26. 如图 12-1 所示，在 中， ， ， 为 的中点，动点 在 边上自由移动，动点 在 边上自由移动． （1）点 的移动过程中， 是否能成为 的等腰三角形？若能，请 指出 为等腰三角形时动点 的位置．若不能，请说明理由． （2）当 时，设 ， ，求 与 之间的函数解析式，写出 的取 值范围． （3）在满足（2）中的条件时，若以 为圆心的圆与 相切（如图 12-2），试探究直线 与 的位置关系，并证明你的结论． 6.(武汉市) 如图①，在平面直角坐标系中，Rt△AOB≌Rt△CDA，且 A(－1，0)、B(0，2)， 抛物线 y＝ax2＋ax－2 经过点 C。(1)求抛物线的解析式；(2)在抛物线(对称轴的右侧)上是否 存在两点 P、Q，使四边形 ABPQ 是正方形？若存在，求点 P、Q 的坐标，若不存在，请说 明理由；(3)如图②，E 为 BC 延长线上一动点，过 A、B、E 三点作⊙O’，连结 AE，在⊙ O’上另有一点 F，且 AF＝AE，AF 交 BC 于点 G，连结 BF。下列结论：①BE＋BF 的值不 变；② ，其中有且只有一个成立，请你判断哪一个结论成立，并证明成立的结论。 ABC△ 2AB AC= = 90A = ∠ O BC E BA F AC E F， OEF△ 45EOF = ∠ OEF△ E F， 45EOF = ∠ BE x= CF y= y x x O AB EF O AG BG AF BF = 图 12-1 A B CO E F 图 12-2 A B CO E F (第 25 题图①) OA B C D x y O x B F A E C O’ G (第 25 题图②) 图(13-2) O3O2O1 A2 B2 P2 O1 A1 P1 O2 O3 B1 图(13-1) 7.(湖北省襄樊市非课改区)26. 如图，在平面直角坐标系中，以点 C(0， 4)为圆心，半径为 4 的圆交 y 轴正半轴于点 A，AB 是⊙C 的切线．动点 P 从点 A 开始沿 AB 方向以每秒 1 个单位长度的速度运动，点 Q 从 O 点开 始沿 x 轴正方向以每秒 4 个单位长度的速度运动，且动点 P、Q 从点 A 和点 O 同时出发，设运动时间为 t(秒)． (1)当 t＝1 时，得到 P1、Q1 两点，求经过 A、P1、Q1 三点的抛物线解 析式及对称轴 l； (2)当 t 为何值时，直线 PQ 与⊙C 相切？并写出此时点 P 和点 Q 的 坐标； (3)在(2)的条件下，抛物线对称轴 l 上存在一点 N，使 NP＋NQ 最小， 求出点 N 的坐标并说明理由． 9、（2006 北京海淀）如图，已知⊙O 的直径 AB 垂直于弦 CD 于 E，连结 AD、BD、OC、 OD，且 OD＝5。 （1）若 ，求 CD 的长； （2）若 ∠ADO：∠EDO＝4：1，求扇形 OAC（阴影部分）的面 积（结果保留 ）。 10、（湖南永州卷）如图，以 为圆心的两个同心圆中，大圆的直径 交小圆于 两点，大圆的弦 切小圆于点 ，过点 作直线 ，垂足为 ，交大圆于 两点．（1）试判断线段 与 的大小关系，并说明理由．（2）求证： ． （3）若 是方程 的两根（ ），求图中阴影部分图形 的周长． 23．（本小题满分 10 分） 已知⊙O1 和⊙O2 的半径都等于 1，O1O2=5，在线段 O1O2 的延长线上取一点 O3，使 O2O3=3，以 O3 为圆心，R=5 为半径作圆。 （1）如图（13-1），⊙O3 与线段 O1O2 相交于点 P1，过点 P1 分别作⊙O1 和⊙O2 的切线 P1A1、P1B1（A1、B1 为切点），连结 O1A1、O2B1，求 P1A1：P1B1 的值。 （2）如图（13-2），若过 O2 作 O2P2⊥O1O2 交 O3 于点 P2，又过点 P2 分别作⊙O1 和⊙O2 的切线 P2A2、P2B2（A2、B2 为切点），求 P2A2：P2B2 的值。 （3）设在⊙O3 上任取一点 P，过点 P 分别作⊙O1 和⊙O2 的切线 PA、PB（A、B 为切 点），由（1）（2）的探究，请提出一个正确命题（不要求证明） sin ∠BAD = 3 5 π O AD M N， AB C C CE AD⊥ E F H， AC BC FC CH AE AO=  FC CH， 2 2 5 4 0x x− + = CH CF> (第 26 题图) A B C x O y l PP1 QQ1 A B C DE 2 3、 （ 湖 南 永 州 卷 ） 如 图 ， 以 O 为 圆 心 的 两 个 同 心 圆 中 ， 大 圆 的 直 径 AD 交 小 圆 于 M N， 两 点 ， 大 圆 的 弦 AB 切 小 圆 于 点 C ， 过 点 C 作 直 线 CE AD⊥ ， 垂 足 为 E ， 交 大 圆 于 F H， 两 点 ． （ 1） 试 判 断 线 段 AC 与 BC 的 大 小 关 系 ， 并 说 明 理 由 ． （ 2） 求 证 ： FC CH AE AO=  ． （ 3） 若 FC CH， 是 方 程 2 2 5 4 0x x− + = 的 两 根 （ CH CF> ） ， 求 图 中 阴 影 部 分 图 形 的 周 长 ． O N H M F