九年级数学下册第三章圆5直线和圆的位置关系第2课时课件北师大版 31页

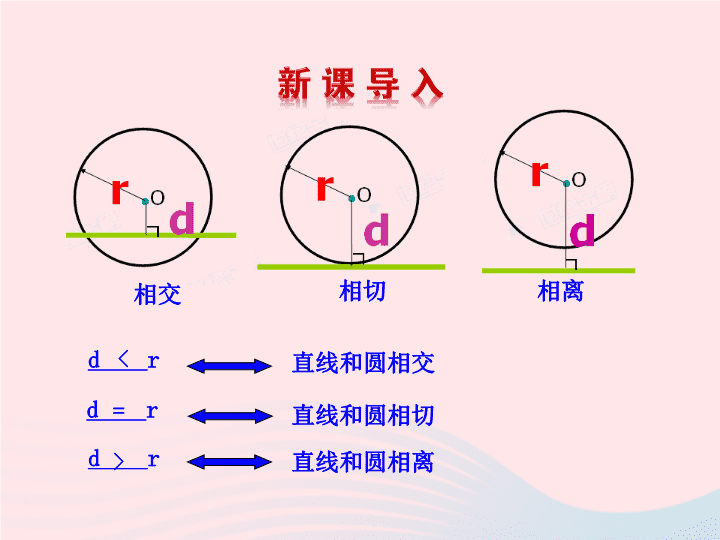
5 直线和圆的位置关系 第 2 课时 1. 通过学习判定一条直线是否为圆的切线 , 训练学生的推理判断能力． 2. 会过圆上一点画圆的切线 , 训练学生的作图能力． 3. 会作三角形的内切圆． 直线和圆相交 d r d r 直线和圆相切 直线和圆相离 d r 相交 相切 　相离 < = > B ● O A l ┓ d α ┏ d α d ┓ 你能写出一个命题来表述这个事实吗 ? 如图 ,AB 是⊙ O 的直径 , 直线 l 经过点 A, l 与 AB 的夹角为∠ α, 当 l 绕点 A 顺时针旋转时 , 圆心 O 到直线 l 的 距离 d 如何变化？ 经过直径的一端 , 并且垂直于这条直径的直线是圆的切线 . C D B ● O A ∵AB 是⊙ O 的直径 , 直线 CD 经过 A 点 , 且 CD⊥AB, ∴ CD 是⊙ O 的切线 . 这个定理实际上就是 d=r 直线和圆相切 的另一种说法 . 探究新知 例 1. 如图 ,AB 是⊙ O 的直径 , ∠ABT=45°,AT=BA ． 求证 :AT 是⊙ O 的切线 . A T B O 证明： AT 经过直径的一端，因此只要证 AT 垂直于 AB 即可，而由已知条件可知 AT=AB ，所以∠ ABT ＝∠ ATB ，又由∠ ABT ＝ 45° ，所以∠ ATB=45°. 由三角形内角和可证∠ TAB=90° ，即 AT⊥AB ，故 AT 是⊙ O 的切线． 【 例题 】 1. 如图 , 已知直线 AB 经过⊙ O 上的点 C, 并且 AO=OB,CA=CB, 那么直线 AB 是⊙ O 的切线吗 ? 解： 连接 OC ， C 经过直径的一端，因此只要证 OC 垂直于 AB 即可，而由已知条件 AO=OB ，所以∠ A ＝∠ B ，又由 AC ＝ BC ，所以 OC⊥AB ．∴直线 AB 是⊙ O 的切线 . 【 跟踪训练 】 Ｏ Ａ Ｂ Ｃ 2 ．如图 , 已知： OA=OB ＝５ ,AB ＝８，以 O 为圆心，以 3 为半径的圆与直线 AB 相切吗？为什么？ 解： 过 O 作 OC⊥AB ，因此只要证 OC=3 即可 , 而由已知条件可知 AO=OB=5 ， AB=8 ，所以 AC ＝ BC=4 ，据勾股定理得 OC=3.∴ ⊙O 与直线 AB 相切 . 从一块三角形材料中 , 能否剪下一个圆 , 使其与各边都相切 ? A B C A B C ● ┓ ┗ ┗ I ● ┓ ● D M N 探究新知 三角形的内切圆作法： （ 1 ）作∠ ABC 、∠ ACB 的平分线 BM 和 CN ，交点为 I. （ 2 ）过点 I 作 ID⊥BC ，垂足为 D. （ 3 ）以 I 为圆心， ID 为半径作⊙ I ， ⊙ I 就是所求 . ∵ 直线 BE 和 CF 只有一个交点 I, 并且点 I 到△ ABC 三边的距离相等 , 因此和 △ ABC 三边都相切的 圆可以作出一个 , 并且只能作一个 . A B C I ● ┓ ● E F 定义： 与三角形三边都相切的圆叫做三角形的内切圆 . 内切圆的圆心叫做三角形的内心，是三角形三条角平分线的交点 . 这样的圆可以作出几个呢 ? 为什么 ? 分别作出锐角三角形 , 直角三角形 , 钝角三角形的内切圆 , 并说明它们内心的位置情况 . 内心均在三角形内部 A B C A B C ● ● ● C A B ┐ 做一做 判断题： 1. 三角形的内心到三角形各个顶点的距离相等（ ） 2. 三角形的外心到三角形各边的距离相等 （ ） 3. 等边三角形的内心和外心重合（ ） 4. 三角形的内心一定在三角形的内部（ ） 错 错 对 对 巩固练习 例 2. 如图，在△ ABC 中，点 O 是内心， （ 1 ）若∠ ABC=50° ， ∠ ACB=70° ， 则∠ BOC 的度数是 . A B C O （ 2 ）若∠ A=80° ，则∠ BOC= . （ 3 ）若∠ BOC=110° ，则∠ A= . 130° 40° 120° 【 例题 】 1. 已知 : 如图 , ⊙O 是 Rt△ABC 的内切圆 ,∠C 是直角 , AC=3,BC=4. 求 ⊙ O 的半径 r . ● A B C ┏ 解：由 Rt△ABC 的三边长与其内切圆半径间的关系得 A B C ● ┏ O b a c ┗ ┓ O D E F ┗ ● 【 跟踪训练 】 ● 2. 已知 : 如图 ,△ABC 的面积 S=4cm 2 , 周长等于 10cm. 求内切圆 ⊙ O 的半径 r. ● A B C ● O ┓ E D ┗ ┗ F 3. 如图，某乡镇在进入镇区的道路交叉口的三角地处建造了一座镇标雕塑，以树立起文明古镇的形象 . 已知雕塑中心 M 到道路三边 AC ， BC ， AB 的距离相等， AC⊥BC ， BC=30 米， AC=40 米 . 求镇标雕塑 中心 M 离道路三边的距离有多远？ A C B 古镇区 镇商业区 镇工业区 M E D F 提示： AC⊥BC ， BC=30 米， AC=40 米得 AB=50 米 . 由 得 M 离道路三边的距离为 10 米 . 1. （兰州 · 中考）如图，等边三角形的内切圆半径为 1 ，那么这个等边三角形的边长为（ ） 答案： D C ． D ． A ． 2 B ． 3 2. （黄冈 · 中考）如图，点 P 为△ ABC 的内心，延长 AP 交△ ABC 的外接圆于 D ，在 AC 延长线上有一点 E ，满足 AD 2 ＝ AB·AE ，求证： DE 是⊙ O 的切线 . 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 证明： 连接 DC ， DO ，并延长 DO 交⊙ O 于 F ，连接 AF. ∵AD 2 ＝ AB · AE ，∠ BAD ＝∠ DAE ， ∴△ BAD∽△DAE ，∴∠ ADB ＝∠ E. 　 又∵∠ ADB ＝∠ ACB ， ∴∠ ACB ＝∠ E ， BC∥DE ， ∴∠ CDE ＝∠ BCD ＝∠ BAD ＝∠ DAC ， 又∵∠ CAF ＝∠ CDF ， ∴∠ FDE ＝∠ CDE+∠CDF ＝∠ DAC+∠CAF ＝∠ DAF ＝ 90° ， 故 DE 是⊙ O 的切线 . 3. （德化 · 中考）如图，在矩形 ABCD 中，点 O 在对角线 AC 上，以 OA 的长为半径的圆 O 与 AD ， AC 分别交于点 E ， F ，且∠ ACB=∠DCE ． (1) 判断直线 CE 与⊙ O 的位置关系， 并证明你的结论 . (2) 若 tan∠ACB= ， BC=2 ， 求⊙ O 的半径 . 【 解析 】 （ 1 ）直线 CE 与⊙ O 相切 . ∵四边形 ABCD 是矩形， ∴ BC∥AD ，∠ ACB=∠DAC ， 又 ∵∠ ACB=∠DCE ， ∴∠ DAC=∠DCE, 连接 OE ，则∠ DAC=∠AEO=∠DCE ， ∵∠ DCE+∠DEC=90° ， ∴∠ AE0+∠DEC=90° ， ∴∠ OEC=90 ° ， ∴直线 CE 与⊙ O 相切 . BC=2 ∴AB=BCtan∠ACB= AC= . 又∵∠ ACB=∠DCE ∴tan∠DCE= ， 设⊙ O 的半径为 r ，则在 Rt△COE 中， 解得： r= . （ 2 ）∵ tan∠ACB= ∴DE=DC • tan∠DCE=1 ， 在 Rt△CDE 中， CE= 得 ， ， 4 ．（临沂 · 中考）如图 ,AB 是半圆的直径 ,O 为圆心， AD ， BD 是半圆的弦，且∠ PDA=∠PBD. （ 1 ）判断直线 PD 是否为⊙ O 的切线，并说明理由 . （ 2 ）如果∠ BDE=60° ， ，求 PA 的长 . 【 解析 】 （ 1 ） PD 是⊙ O 的切线 . 连接 OD,∵OB=OD, ∴∠ODB=∠PBD. 又∵∠ PDA=∠PBD.∴∠ODB=∠PDA. 又∵ AB 是半圆的直径，∴∠ ADB=90°. 即∠ ODB+∠ODA=90°. ∴∠ODA+∠PDA=90°, 即 OD⊥PD.∴PD 是⊙ O 的切线 . （ 2 ）∵∠ BDE=60°,∠ODE=90°,∠ADB=90°, ∴∠ODB=30°,∠ODA=60°. ∵OA=OD, ∴△AOD 是等边三角形 . ∴∠POD=60°. ∴∠P=∠PDA=30°. 在直角△ PDO 中，设 OD=x, ∴ ∴x 1 =1,x 2 =-1 （不合题意，舍去） ∴ PA=1. 【 规律方法 】 证明直线是否是圆的切线有两种辅助线的作法 ：（ 1 ） 过圆心作已知直线的垂线，判定距离等于半径；（ 2 ）连接圆心与圆上的点，证垂直 . 本节课学习了以下内容： 1 ．探索切线的判定条件． 2 ．作三角形的内切圆． 3 ．了解三角形的内切圆，三角形的内心的概念． 风再大也会停，路再长也要行。当你到达平静的港湾，找到美丽的城堡，才能真切感受到：坚持是如此重要。